Linear regression is one of the most important methods of data analysis. It serves the determination of model parameters, model fitting, assessing the importance of influencing factors, and prediction, in all areas of human, natural and economic sciences. Computer scientists who work closely with people from these areas will definitely come across regression models.
The aim of this chapter is a first introduction into the subject. We deduce the coefficients of the regression models using the method of least squares to minimise the errors. We will only employ methods of descriptive data analysis. We do not touch upon the more advanced probabilistic approaches which are topics of statistics. For that, as well as for nonlinear regression, we refer to the specialised literature.
We start with simple (or univariate) linear regression—a model with a single input and a single output quantity—and explain the basic ideas of analysis of variance for model evaluation. Then we turn to multiple (or multivariate) linear regression with several input quantities. The chapter closes with a descriptive approach to determine the influence of the individual coefficients.
18.1 Simple Linear Regression
A first glance at the basic idea of linear regression was already given in Sect. 8.3. In extension to this, we will now allow more general models, in particular regression lines with nonzero intercept.
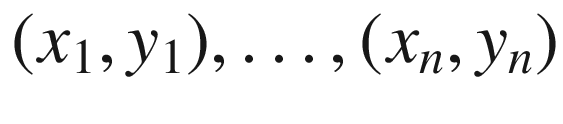 , obtained as observations or
measurements. Geometrically they form a scatter plot in the
plane. The values
, obtained as observations or
measurements. Geometrically they form a scatter plot in the
plane. The values  and
and  may appear repeatedly in this list of
data. In particular, for a given
may appear repeatedly in this list of
data. In particular, for a given  there can be data points with
different values
there can be data points with
different values  . The general task of linear
regression is to fit the graph of a function
. The general task of linear
regression is to fit the graph of a function

 . Here the shape functions
. Here the shape functions  are given and the (unknown)
coefficients
are given and the (unknown)
coefficients  are to be determined such that the
sum of squares of the errors is minimal
(method of least squares):
are to be determined such that the
sum of squares of the errors is minimal
(method of least squares):

 . The choice of the shape functions
ensues either from a possible theoretical model or empirically,
where different possibilities are subjected to statistical tests.
The choice is made, for example, according to the proportion of
data variability which is explained by the regression—more about
that in Sect. 18.4. The standard question of (simple or
univariate) linear regression is to fit a
linear model
. The choice of the shape functions
ensues either from a possible theoretical model or empirically,
where different possibilities are subjected to statistical tests.
The choice is made, for example, according to the proportion of
data variability which is explained by the regression—more about
that in Sect. 18.4. The standard question of (simple or
univariate) linear regression is to fit a
linear model


Scatter plot height/weight, line of best fit, best parabola
Example 18.1
 computer science students at the
University of Innsbruck in 2002 yielded the data depicted in Fig.
18.1. Here
x denotes the height [cm] and
y the weight [kg] of the
students. The left picture in Fig. 18.1 shows the regression
line
computer science students at the
University of Innsbruck in 2002 yielded the data depicted in Fig.
18.1. Here
x denotes the height [cm] and
y the weight [kg] of the
students. The left picture in Fig. 18.1 shows the regression
line  , the right one a fitted quadratic
parabola of the form
, the right one a fitted quadratic
parabola of the form

 was set to zero in the linear
model.
was set to zero in the linear
model.


 ,
, 



Scatter plot height of fathers/height of the sons, regression line

 and
and  . In general, the given data will not
exactly lie on a straight line but deviate by
. In general, the given data will not
exactly lie on a straight line but deviate by  , i.e.,
, i.e.,


Linear model and error 
 for
for  . This is achieved through minimising
the sum of squares of the errors
. This is achieved through minimising
the sum of squares of the errors

 solve the minimisation problem
solve the minimisation problem

 and
and  by setting the partial derivatives of
L with respect to
by setting the partial derivatives of
L with respect to  and
and  to zero:
to zero:

 , the
so-called normal equations
, the
so-called normal equations

Proposition 18.2
 ,
,  are different. Then the normal
equations have a unique solution
are different. Then the normal
equations have a unique solution

 of the errors.
of the errors.Proof
With the notations  and
and  the determinant of the normal
equations is
the determinant of the normal
equations is  . For vectors of length
. For vectors of length  and
and  we know that
we know that  , see Appendix A.4, and thus
, see Appendix A.4, and thus
 . This relation, however, is valid in
any dimension n (see for
instance [2, Chap. VI, Theorem 1.1]), and equality can only occur
if
. This relation, however, is valid in
any dimension n (see for
instance [2, Chap. VI, Theorem 1.1]), and equality can only occur
if  is parallel to
is parallel to  , so all components
, so all components  are equal. As this possibility was
excluded, the determinant of the normal equations is greater than
zero and the solution formula is obtained by a simple
calculation.
are equal. As this possibility was
excluded, the determinant of the normal equations is greater than
zero and the solution formula is obtained by a simple
calculation.
 , we compute the Hessian matrix
, we compute the Hessian matrix

 and
and  are both positive. According to
Proposition 15.28, L has an isolated local minimum at the
point
are both positive. According to
Proposition 15.28, L has an isolated local minimum at the
point  . Due to the uniqueness of the
solution, this is the only minimum of L.
. Due to the uniqueness of the
solution, this is the only minimum of L. 
 -values in the data set is not a
restriction since otherwise the regression problem is not
meaningful. The result of the regression
is the predicted regression
line
-values in the data set is not a
restriction since otherwise the regression problem is not
meaningful. The result of the regression
is the predicted regression
line


 are called residuals
are called residuals


Linear model, prediction, residual
With the above specifications, the
deterministic regression model
is completed. In the statistical
regression model the errors  are interpreted as random variables
with mean zero. Under further probabilistic assumptions the model
is made accessible to statistical tests and diagnostic procedures.
As mentioned in the introduction, we will not pursue this path here
but remain in the framework of descriptive data analysis.
are interpreted as random variables
with mean zero. Under further probabilistic assumptions the model
is made accessible to statistical tests and diagnostic procedures.
As mentioned in the introduction, we will not pursue this path here
but remain in the framework of descriptive data analysis.







Example 18.3
 height and
height and  weight can be found in the M-file
mat08_3.m;
the matrix
weight can be found in the M-file
mat08_3.m;
the matrix  is generated in MATLAB by
is generated in MATLAB by


 permits a more stable calculation in
MATLAB. In our
case the result is
permits a more stable calculation in
MATLAB. In our
case the result is

18.2 Rudiments of the Analysis of Variance
First indications for the quality of fit of the linear model can be obtained from the analysis of variance (ANOVA), which also forms the basis for more advanced statistical test procedures.
 is
is

 from the mean value
from the mean value  is
is  . The total sum of squares or total variability of the data is
. The total sum of squares or total variability of the data is


 is the deviation of the predicted
value from the mean value, and
is the deviation of the predicted
value from the mean value, and

 are the residuals, and
are the residuals, and

- (a)
The data values
 themselves already lie on a straight
line. Then all
themselves already lie on a straight
line. Then all  and thus
and thus  ,
,  , and the regression model describes
the data record exactly.
, and the regression model describes
the data record exactly. - (b)
The data values are in no linear relation. Then the line of best fit is the horizontal line through the mean value (see Exercise 13 of Chap. 8), so
 for all i and hence
for all i and hence  ,
,  . This means that the regression model
does not offer any indication for a linear relation between the
values.
. This means that the regression model
does not offer any indication for a linear relation between the
values.
The basis of these considerations is the validity of the following formula.
Proposition 18.4
(Partitioning of total
variability)  .
.
Proof

 , and the matrix identity
, and the matrix identity  . We have
. We have

 and the transposition formula
and the transposition formula
 . The relation
. The relation  implies in particular
implies in particular  . Since the first line of
. Since the first line of  consists of ones only, it follows
that
consists of ones only, it follows
that  and thus
and thus

 and
and  results in the sought after formula.
results in the sought after formula.



 is called coefficient of determination and
measures the fraction of variability
explained by the regression. In the limiting case of an exact fit,
where the regression line passes through all data points, we have
is called coefficient of determination and
measures the fraction of variability
explained by the regression. In the limiting case of an exact fit,
where the regression line passes through all data points, we have
 and thus
and thus  . A small value of
. A small value of  indicates that the linear model does
not fit the data.
indicates that the linear model does
not fit the data.Remark 18.5
An essential point in the proof of
Proposition 18.4 was the property of  that its first line was composed of
ones only. This is a consequence of the fact that
that its first line was composed of
ones only. This is a consequence of the fact that  was a model parameter. In the
regression where a straight line through the origin is used (see
Sect. 8.3) this is not the case. For a
regression which does not have
was a model parameter. In the
regression where a straight line through the origin is used (see
Sect. 8.3) this is not the case. For a
regression which does not have  as a parameter the variance partition
is not valid and the coefficient of determination is
meaningless.
as a parameter the variance partition
is not valid and the coefficient of determination is
meaningless.
Example 18.6


 is a clear indication that height and
weight are not in a linear relation.
is a clear indication that height and
weight are not in a linear relation.Example 18.7
 of a bounded subset A of
of a bounded subset A of  was defined by the limit
was defined by the limit

 denoted the smallest number of
squares of side length
denoted the smallest number of
squares of side length  needed to cover A. For the experimental determination of
the dimension of a fractal set A, one rasters the plane with different
mesh sizes
needed to cover A. For the experimental determination of
the dimension of a fractal set A, one rasters the plane with different
mesh sizes  and determines the number
and determines the number
 of boxes that have a non-empty
intersection with the fractal. As explained in
Sect. 9.1, one uses the approximation
of boxes that have a non-empty
intersection with the fractal. As explained in
Sect. 9.1, one uses the approximation



 ,
,  . The regression coefficient
. The regression coefficient
 can be used as an estimate for the
fractal dimension d.
can be used as an estimate for the
fractal dimension d.|
|
4 |
8 |
12 |
16 |
24 |
32 |
|---|---|---|---|---|---|---|
|
|
16 |
48 |
90 |
120 |
192 |
283 |
 ,
,  yields the coefficients
yields the coefficients


 .
.
Fractal dimension of the coastline of Great Britain
A word of caution is in order. Data
analysis can only supply indications, but never a proof that a
model is correct. Even if we choose among a number of wrong models
the one with the largest  , this model will not become correct.
A healthy amount of skepticism with respect to purely empirically
inferred relations is advisable; models should always be critically
questioned. Scientific progress arises from the interplay between
the invention of models and their experimental validation through
data.
, this model will not become correct.
A healthy amount of skepticism with respect to purely empirically
inferred relations is advisable; models should always be critically
questioned. Scientific progress arises from the interplay between
the invention of models and their experimental validation through
data.
18.3 Multiple Linear Regression
 . We emphasise that the notation with
respect to Sect. 18.1 is changed; there
. We emphasise that the notation with
respect to Sect. 18.1 is changed; there  denoted the ith data value, and now
denoted the ith data value, and now  refers to the ith regressor variable. The measurements
of the ith regressor variable
are now denoted with two indices, namely
refers to the ith regressor variable. The measurements
of the ith regressor variable
are now denoted with two indices, namely  . In total, there are
. In total, there are  data values. We again look for a
linear model
data values. We again look for a
linear model

 .
.

Multiple linear regression through a scatter plot in space
Example 18.8
A vending machine company wants to
analyse the delivery time, i.e., the time span y which a driver needs to refill a
machine. The most important parameters are the number  of refilled product units and the
distance
of refilled product units and the
distance  walked by the driver. The results of
an observation of 25 services are given in the M-file mat18_3.m. The data
values are taken from [19]. The observations
walked by the driver. The results of
an observation of 25 services are given in the M-file mat18_3.m. The data
values are taken from [19]. The observations  with the corresponding service times
with the corresponding service times
 yield a scatter plot in space to
which a plane of the form
yield a scatter plot in space to
which a plane of the form  should be fitted (Fig. 18.6; use the M-file
mat18_4.m
for visualisation).
should be fitted (Fig. 18.6; use the M-file
mat18_4.m
for visualisation).
Remark 18.9
 is simple linear regression with
several nonlinear form functions (as mentioned in
Sect. 18.1), i.e.,
is simple linear regression with
several nonlinear form functions (as mentioned in
Sect. 18.1), i.e.,

 are considered as regressor
variables. In particular one can allow polynomial models
are considered as regressor
variables. In particular one can allow polynomial models



 is to be approximated by
is to be approximated by

 . The estimated coefficients
. The estimated coefficients
 are again obtained as the solution of
the minimisation problem
are again obtained as the solution of
the minimisation problem







Example 18.10




 of the variability of the data is not
explained by the regression, a very satisfactory goodness of
fit.
of the variability of the data is not
explained by the regression, a very satisfactory goodness of
fit.18.4 Model Fitting and Variable Selection
 and
and  , i.e., the model
, i.e., the model

 be eliminated subsequently? It is not
desirable to have too many variables in the model. If there are as
many variables as data points, then one can fit the regression
exactly through the data and the model would loose its predictive
power. A criterion will definitely be to reach a value of
be eliminated subsequently? It is not
desirable to have too many variables in the model. If there are as
many variables as data points, then one can fit the regression
exactly through the data and the model would loose its predictive
power. A criterion will definitely be to reach a value of
 which is as large as possible.
Another aim is to eliminate variables that do not contribute
essentially to the total variability. An algorithmic procedure for
identifying these variables is the sequential partitioning of total
variability.
which is as large as possible.
Another aim is to eliminate variables that do not contribute
essentially to the total variability. An algorithmic procedure for
identifying these variables is the sequential partitioning of total
variability. :
:

 , since in the initial model
, since in the initial model
 The additional explanatory power of
the variable
The additional explanatory power of
the variable  is measured by
is measured by

 (if
(if  is already in the model) by
is already in the model) by

 (if
(if  are in the model) by
are in the model) by



 , under the condition that the
variables
, under the condition that the
variables  are already included in the model.
This partial coefficient of determination depends on the order of
the added variables. This dependency can be eliminated by averaging
over all possible sequences of variables.
are already included in the model.
This partial coefficient of determination depends on the order of
the added variables. This dependency can be eliminated by averaging
over all possible sequences of variables.Average
explanatory power of individual coefficients. One first
computes all possible sequential, partial coefficients of
determination which can be obtained by adding the variable
 to all possible combinations of the
already included variables. Summing up these coefficients and
dividing the result by the total number of possibilities, one
obtains a measure for the contribution of the variable
to all possible combinations of the
already included variables. Summing up these coefficients and
dividing the result by the total number of possibilities, one
obtains a measure for the contribution of the variable  to the explanatory power of the
model.
to the explanatory power of the
model.
Average over orderings was proposed by [16]; further details and advanced considerations can be found, for instance, in [8, 10]. The concept does not use probabilistically motivated indicators. Instead it is based on the data and on combinatorics, thus belongs to descriptive data analysis. Such descriptive methods, in contrast to the commonly used statistical hypothesis testing, do not require additional assumptions which may be difficult to justify.
Example 18.11


 ,
,  in the first and
in the first and  ,
,  in the second case. With the already
computed values of the bivariate model
in the second case. With the already
computed values of the bivariate model



 (or of the coefficient
(or of the coefficient  ) is
) is

 is
is

 stay unexplained. The result is
represented in Fig. 18.7.
stay unexplained. The result is
represented in Fig. 18.7.
Average explanatory powers of the individual variables
 . In the left column of the table
there are the
. In the left column of the table
there are the  permutations of
permutations of  , the other columns list the
sequentially obtained values of
, the other columns list the
sequentially obtained values of  .
.

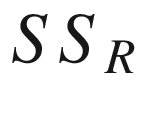 , so that the sum of all entries is
equal to
, so that the sum of all entries is
equal to  . Note that amongst the 18
. Note that amongst the 18
 -values there are actually only 12
different ones.
-values there are actually only 12
different ones. is defined by
is defined by  , where
, where



 ) and for a discussion of the
significance of the average explanatory power, we refer to the
literature quoted above. The algorithm is implemented in the applet
Linear regression.
) and for a discussion of the
significance of the average explanatory power, we refer to the
literature quoted above. The algorithm is implemented in the applet
Linear regression.Experiment 18.12
Open the applet Linear regression and load data set
number 9. It contains experimental data quantifying the
influence of different aggregates on a mixture of concrete. The
meaning of the output variables  through
through  and the input variables
and the input variables  through
through  is explained in the online
description of the applet. Experiment with different selections of
the variables of the model. An interesting initial model is
obtained, for example, by choosing
is explained in the online
description of the applet. Experiment with different selections of
the variables of the model. An interesting initial model is
obtained, for example, by choosing  as independent and
as independent and  as dependent variable; then remove
variables with low explanatory power and draw a pie chart.
as dependent variable; then remove
variables with low explanatory power and draw a pie chart.
18.5 Exercises
- 1.
-
The total consumption of electric energy in Austria 1970–2015 is given in Table 18.1 (from [26, Table 22.13]). The task is to carry out a linear regression of the form
 through the data.
through the data.
- (a)
-
Write down the matrix
 explicitly and compute the
coefficients
explicitly and compute the
coefficients ![$$\widehat{\varvec{\beta }}= [\widehat{\beta }_0, \widehat{\beta }_1]^\mathsf{T}$$](/epubstore/O/M-Oberguggenberger/Analysis-For-Computer-Scientists/OEBPS/images/215236_2_En_18_Chapter/215236_2_En_18_Chapter_TeX_IEq159.png) using the MATLAB command
using the MATLAB command  .
. - (b)
-
Check the goodness of fit by computing
 . Plot a scatter diagram with the
fitted straight line. Compute the forecast
. Plot a scatter diagram with the
fitted straight line. Compute the forecast  for 2020.
for 2020.
Table 18.1Electric energy consumption in Austria, year
 , consumption
, consumption  [GWh]
[GWh]
1970
1980
1990
2000
2005
2010
2013
2014
2015

23.908
37.473
48.529
58.512
66.083
68.931
69.934
68.918
69.747
- 2.
-
A sample of
 civil engineering students at the
University of Innsbruck in the year 1998 gave the values for
civil engineering students at the
University of Innsbruck in the year 1998 gave the values for
 height [cm] and
height [cm] and  weight [kg], listed in the M-file
mat18_ex2.m. Compute
the regression line
weight [kg], listed in the M-file
mat18_ex2.m. Compute
the regression line  , plot the scatter diagram and
calculate the coefficient of determination
, plot the scatter diagram and
calculate the coefficient of determination  .
. - 3.
-
Solve Exercise 1 using Excel.
- 4.
-
Solve Exercise 1 using the statistics package SPSS.
Hint. Enter the data in the worksheet Data View; the names of the variables and their properties can be defined in the worksheet Variable View. Go to Analyze
 Regression
Regression  Linear.
Linear. - 5.
-
The stock of buildings in Austria 1869–2011 is given in the M-file mat18_ex5.m (data from [26, Table 12.01]). Compute the regression line
 and the regression parabola
and the regression parabola
 through the data and test which model
fits better, using the coefficient of determination
through the data and test which model
fits better, using the coefficient of determination  .
. - 6.
-
The monthly share index for four breweries from November 1999 to November 2000 is given in the M-file mat18_ex6.m (November 1999
 , from the Austrian magazine profil
46/2000). Fit a univariate linear model
, from the Austrian magazine profil
46/2000). Fit a univariate linear model  to each of the four data sets
to each of the four data sets
 , plot the results in four equally
scaled windows, evaluate the results by computing
, plot the results in four equally
scaled windows, evaluate the results by computing  and check whether the caption
provided by profil is justified by the data. For the calculation
you may use the MATLAB program mat18_1.m.
and check whether the caption
provided by profil is justified by the data. For the calculation
you may use the MATLAB program mat18_1.m.Hint. A solution is suggested in the M-file mat18_exsol6.m.
- 7.
-
Continuation of Exercise 5, stock of buildings in Austria. Fit the modeland compute

 and
and  . Further, analyse the increase of
explanatory power through adding the respective missing variable in
the models of Exercise 5, i.e., compute
. Further, analyse the increase of
explanatory power through adding the respective missing variable in
the models of Exercise 5, i.e., compute  and
and  as well as the average explanatory
power of the individual coefficients. Compare with the result for
data set number 5 in the applet Linear regression.
as well as the average explanatory
power of the individual coefficients. Compare with the result for
data set number 5 in the applet Linear regression. - 8.
-
The M-file mat18_ex8.m contains the mileage per gallon y of 30 cars depending on the engine displacement
 , the horsepower
, the horsepower  , the overall length
, the overall length  and the weight
and the weight  of the vehicle (from: Motor Trend
1975, according to [19]). Fit the linear model
and estimate the explanatory power of the individual coefficients through a simple sequential analysis
of the vehicle (from: Motor Trend
1975, according to [19]). Fit the linear model
and estimate the explanatory power of the individual coefficients through a simple sequential analysis Compare your result with the average explanatory power of the coefficients for data set number 2 in the applet Linear regression.
Compare your result with the average explanatory power of the coefficients for data set number 2 in the applet Linear regression.
Hint. A suggested solution is given in the M-file mat18_exsol8.m.
- 9.
-
Check the results of Exercises 2 and 6 using the applet Linear regression (data sets 1 and 4); likewise for the Examples 18.1 and 18.8 with the data sets 8 and 3. In particular, investigate in data set 8 whether height, weight and the risk of breaking a leg are in any linear relation.
- 10.
-
Continuation of Exercise 14 from Sect. 8.4. A more accurate linear approximation to the relation between shear strength
 and normal stress
and normal stress  is delivered by Coulomb’s model
is delivered by Coulomb’s model
 where
where  and c [kPa] is interpreted as cohesion.
Recompute the regression model of Exercise 14 in
Sect. 8.4 with nonzero intercept. Check
that the resulting cohesion is indeed small as compared to the
applied stresses, and compare the resulting friction angles.
and c [kPa] is interpreted as cohesion.
Recompute the regression model of Exercise 14 in
Sect. 8.4 with nonzero intercept. Check
that the resulting cohesion is indeed small as compared to the
applied stresses, and compare the resulting friction angles. - 11.
-
(Change point analysis) The consumer prize data from Example 8.21 suggest that there might be a change in the slope of the regression line around the year 2013, see also Fig. 8.9. Given data
 with ordered data points
with ordered data points  , phenomena of this type can be
modelled by a piecewise linear regression
If the slopes
, phenomena of this type can be
modelled by a piecewise linear regression
If the slopes
 and
and  are different,
are different,  is called a change point. A
change point can be detected by fitting models
and varying the index m between 2 and
is called a change point. A
change point can be detected by fitting models
and varying the index m between 2 and
 until a two-line model with the
smallest total residual sum of squares
until a two-line model with the
smallest total residual sum of squares  is found. The change point
is found. The change point
 is the point of intersection of the
two predicted lines. (If the overall one-line model has the
smallest
is the point of intersection of the
two predicted lines. (If the overall one-line model has the
smallest  , there is no change point.) Find out
whether there is a change point in the data of Example 8.21. If so, locate it and use the
two-line model to predict the consumer price index for 2017.
, there is no change point.) Find out
whether there is a change point in the data of Example 8.21. If so, locate it and use the
two-line model to predict the consumer price index for 2017. - 12.
-
Atmospheric
 concentration has been recorded at
Mauna Loa, Hawai, since 1958. The yearly averages (1959–2008) in
ppm can be found in the MATLAB program mat18_ex12.m; the data
are from [14].
concentration has been recorded at
Mauna Loa, Hawai, since 1958. The yearly averages (1959–2008) in
ppm can be found in the MATLAB program mat18_ex12.m; the data
are from [14].
- (a)
-
Fit an exponential model
 to the data and compare the
prediction with the actual data (2017: 406.53 ppm).
to the data and compare the
prediction with the actual data (2017: 406.53 ppm).Hint. Taking logarithms leads to the linear model
 with
with  ,
,  ,
,  . Estimate the coefficients
. Estimate the coefficients
 ,
,  and compute
and compute  ,
,  as well as the prediction for
y.
as well as the prediction for
y. - (b)
-
Fit a square exponential model
 to the data and check whether this
yields a better fit and prediction.
to the data and check whether this
yields a better fit and prediction.

