Contrastes de hipótesis frecuentemente utilizados: fórmulas y ejemplos

En este capítulo

Analizar a fondo los contrastes de hipótesis más utilizados

Calcular sus estadísticos de contraste

Utilizar los resultados para tomar decisiones con conocimiento de causa

Desde los anuncios de productos hasta las noticias sobre recientes avances en medicina, nos encontramos a todas horas con afirmaciones referidas a una o más poblaciones. Por ejemplo: “Prometemos entregar su paquete en dos días o menos” o “Dos estudios recientes demuestran que una dieta rica en fibra puede reducir en el 20% el riesgo de padecer cáncer de colon”. Cuando alguien hace una afirmación (también llamada hipótesis nula) sobre una población (por ejemplo todos los paquetes enviados, o todos los adultos), puedes contrastar esa afirmación mediante lo que en estadística se denomina un contraste de hipótesis.

Para realizar un contraste de hipótesis tienes que formular las hipótesis (una afirmación y su alternativa), recopilar datos, calcular los estadísticos relevantes y utilizar esos estadísticos para decidir si la afirmación es verdadera.

En este capítulo te presento las fórmulas utilizadas para los contrastes de hipótesis más comunes, explico los cálculos necesarios y comento algunos ejemplos.

Si necesitas más información sobre contrastes de hipótesis (definir hipótesis, comprender los estadísticos de contraste, valores p, niveles de significación y errores de tipo 1 y de tipo 2), ve al capítulo 14. Allí desarrollo todos los conceptos generales de los contrastes de hipótesis. Este capítulo se centra en su aplicación.

Contrastar una media poblacional

Cuando la variable es numérica (por ejemplo edad, ingresos, tiempo, etc.) y únicamente se estudia una población o grupo (por ejemplo todas las familias de Estados Unidos o todos los estudiantes universitarios), para analizar o cuestionar una afirmación referida a la media poblacional se utiliza el contraste de hipótesis descrito en este apartado. Por ejemplo, un psicólogo infantil dice que las madres trabajadoras dedican, en promedio, 11 minutos diarios a hablar con sus hijos (según ese mismo psicólogo, los padres dedican un tiempo medio de 8 minutos). La variable (el tiempo) es numérica, y la población son todas las madres trabajadoras. Si utilizamos la notación estadística, μ representa el número de minutos diarios que todas las madres trabajadoras dedican a hablar con sus hijos, en promedio.

La hipótesis nula es que la media poblacional, μ, es igual a un determinado valor propuesto, μ₀. La notación de la hipótesis nula es H₀: μ = μ₀. Así pues, la hipótesis nula de nuestro ejemplo es H₀: μ = 11 minutos, y μ₀ es 11. Las tres posibilidades para la hipótesis alternativa, H_a, son μ ≠ 11, μ < 11 y μ > 11, dependiendo de lo que pretendas demostrar (en el capítulo 14 encontrarás más información sobre hipótesis alternativas). Si sospechas que el tiempo medio que dedican las madres a hablar con sus hijos es superior a 11 minutos, elegirás la hipótesis alternativa H_a: μ > 11.

Para contrastar la afirmación, comparas la media obtenida a partir de tu muestra () con la media indicada en H₀ (μ₀). Para que la comparación sea correcta, determinas la diferencia entre ambos valores y divides por el error estándar para tener en cuenta el hecho de que los resultados muestrales están sujetos a variación. (En el capítulo 12 encontrarás toda la información que necesitas sobre el error estándar.) Este resultado es tu estadístico de contraste. En el caso de un contraste de hipótesis para la media poblacional, el estadístico de contraste es (si se cumplen ciertas condiciones) un valor z (un valor de la distribución Z; ver el capítulo 9).

Por tanto, puedes buscar tu estadístico de contraste en la tabla apropiada (en este caso la tabla Z, incluida en el apéndice) y ver cuál es la probabilidad de que esta diferencia entre tu media muestral y la media poblacional propuesta pueda ocurrir realmente si la afirmación es verdadera.

El estadístico de contraste para contrastar una media poblacional (si se cumplen ciertas condiciones) es:

donde es la media muestral, σ es la desviación estándar de la población (en este caso supondremos que es un número conocido), y z es un valor de la distribución Z. Para calcular el estadístico de contraste, haz lo siguiente:

1. Calcula la media muestral, .

2. Encuentra - μ₀.

3. Calcula el error estándar: .

4. Divide el resultado del paso 2 por el error estándar calculado en el paso 3.

Las condiciones para utilizar este estadístico de contraste son, primero, que se conozca la desviación estándar de la población, σ, y segundo, que la población tenga una distribución normal o bien el tamaño muestral sea suficientemente grande para aplicar el teorema del límite central (n>30); sobre ello hablamos en el capítulo 11.

Para nuestro ejemplo, supondremos que una muestra aleatoria de 100 madres trabajadoras dedicaron una media de 11,5 minutos diarios a hablar con sus hijos (supondremos también que, según estudios anteriores, la desviación estándar de la población es 2,3 minutos).

1. Nos dicen que es 11,5, n = 100 y σ es 2,3.

2. Calcula 11,5 – 11 = +0,5.

3. Para calcular el error estándar divides 2,3 por la raíz cuadrada de 100 (que es 10), y te da 0,23.

4. Ahora divides +0,5 por 0,23. El resultado de esta operación es 2,17. Éste es tu estadístico de contraste. Significa que tu media muestral está 2,17 errores estándares por encima de la media poblacional propuesta.

El contraste de hipótesis cuestiona la afirmación que se está haciendo sobre la población (en este caso, la media poblacional); esa afirmación está representada por la hipótesis nula, H₀. Si la muestra te proporciona suficientes indicios en contra de la afirmación, rechazas H₀.

Para decidir si tienes indicios suficientes para rechazar H₀, calcula el valor p buscando tu estadístico de contraste (en este caso 2,17) en la distribución normal estándar (distribución Z) —consulta la tabla Z en el apéndice— y resta de 1 la probabilidad hallada (restas de 1 porque tu H_a es una hipótesis del tipo “mayor que”, y la tabla contiene probabilidades del tipo “menor que”).

Para este ejemplo, si buscas el estadístico de contraste (2,17) en la tabla Z verás que la probabilidad (“menor que”) es 0,985, de manera que el valor p es 1 –0,985 = 0,015. Este valor está bastante por debajo del nivel de significación (típico) de 0,05, lo cual significa que tus resultados muestrales se considerarían fuera de lo normal si la afirmación (de 11 minutos) fuera verdadera. Por tanto, rechazas la afirmación (H₀: μ = 11 minutos). Tus resultados apoyan la hipótesis alternativa H_a: μ > 11. Según los datos que has obtenido, los 11 minutos diarios que según el psicólogo infantil dedican las madres a hablar con sus hijos son un valor demasiado bajo; la media real es más alta.

En el capítulo 14 encontrarás más información sobre cómo calcular valores p para las alternativas “menor que” y “distinto de”.

Muestras pequeñas y desviaciones estándar desconocidas: la prueba t

Hay dos casos en los que no puedes utilizar la distribución Z para un estadístico de contraste cuando quieres contrastar una media poblacional. El primer caso es cuando el tamaño muestral es pequeño (y cuando digo pequeño, quiero decir inferior a 30, aproximadamente), y el segundo caso es cuando la desviación estándar de la población, σ, se desconoce, y entonces hay que estimarla utilizando la desviación estándar de la muestra, s. En ambos casos tienes menos información fiable sobre la cual basar tus conclusiones, de manera que debes pagar un peaje utilizando una distribución que presenta más variabilidad en las colas que la distribución Z. Aquí es donde entra en escena la distribución t. (En el capítulo 10 encontrarás más información sobre la distribución t, incluida su relación con la distribución Z.)

Un contraste de hipótesis para una media poblacional que utilice la distribución t se llama prueba t. La fórmula para el estadístico de contraste en este caso es:

,

en la que t_n-1 es un valor de la distribución t que tiene n–1 grados de libertad.

Si te fijas, verás que es igual que el estadístico de contraste para el caso de una muestra grande o una distribución normal (lee el apartado “Contrastar una media poblacional”), salvo que σ es desconocida, de manera que la sustituyes por la desviación estándar de la muestra, s, y utilizas un valor t en lugar de un valor z.

Como la distribución t tiene las colas más gruesas que la distribución Z, el valor p obtenido con la distribución t es más grande que el que habrías obtenido con la distribución normal estándar (distribución Z) para el mismo estadístico de contraste. Un valor p más grande significa una probabilidad menor de rechazar H₀. Tener pocos datos y no conocer la desviación estándar de la población aumenta la dificultad de determinar la hipótesis nula.

Aplicación práctica de la prueba t

Supongamos que una empresa de mensajería asegura que entrega sus paquetes en el plazo de dos días, en promedio, y tú sospechas que tarda más tiempo. Las hipótesis son H₀: μ = 2 contra H_a: μ > 2. Para contrastar esta afirmación, tomas una muestra aleatoria de 10 paquetes y anotas los tiempos de entrega. Averiguas que la media muestral es = 2,3 días y la desviación estándar de la muestra es 0,35 días (como desconoces la desviación estándar de la población, σ, la estimas con s, la desviación estándar de la muestra). Este problema se resuelve con la prueba t.

Como el tamaño muestral es pequeño (n =10 es mucho menos que 30) y la desviación estándar de la población es desconocida, el estadístico de contraste tiene una distribución t. Sus grados de libertad son 10 – 1 = 9. La fórmula para el estadístico de contraste (nos referiremos a él como valor t) es:

Para calcular el valor p, ve a la tabla t (incluida en el apéndice) y busca la fila que corresponde a gl = 9. Tu estadístico de contraste (2,71) se encuentra entre dos valores de la fila correspondiente a gl = 9 en la tabla t: 2,26 y 2,82 (redondeando a dos cifras decimales). Para calcular el valor p para tu estadístico de contraste, busca las columnas correspondientes a esos dos números. El número 2,26 aparece en la columna 0,025 y el número 2,82 aparece en la columna 0,010; por tanto, sabes que el valor p para tu estadístico de contraste se encuentra entre 0,025 y 0,010 (es decir, 0,010 < valor p < 0,025).

Utilizando la tabla t no puedes saber el número exacto que corresponde al valor p, pero como 0,01 y 0,025 son más pequeños que tu nivel de significación (0,05), rechazas H₀; la muestra te proporciona suficientes indicios para decir que los paquetes no se están entregando en dos días, sino que el tiempo medio de entrega es en realidad superior a dos días.

La tabla t (incluida en el apéndice) no incluye todos los valores t posibles; sólo tienes que buscar los dos números más próximos al tuyo por ambos lados y ver en qué columnas aparecen. El valor p se encuentra entre los valores p de esos números (si tu estadístico de contraste es más grande que todos los valores t de la fila correspondiente de la tabla t, utiliza el último; tu valor p será más pequeño que la probabilidad de ese último valor).

Naturalmente, puedes utilizar un programa informático, si lo tienes, para calcular los valores p exactos para cualquier estadístico de contraste; de este modo verías que el valor p exacto en este caso es 0,012.

Relacionar t y Z

La penúltima línea de la tabla t muestra los valores de la distribución normal estándar (distribución Z) que corresponden a las probabilidades indicadas en la cabecera de cada columna. Ahora elige una columna de la tabla y mira los valores t. Observa que, a medida que los grados de libertad de la distribución t aumentan, los valores t se acercan más y más a esa fila de la tabla donde están los valores z.

Esto confirma un resultado hallado en el capítulo 10: a medida que el tamaño muestral (y, por tanto, los grados de libertad) aumenta, la distribución t se asemeja cada vez más a la distribución Z, de modo que los valores p de sus contrastes de hipótesis son prácticamente iguales cuando el tamaño muestral es grande. Y ni siquiera es necesario que esos tamaños muestrales sean muy grandes para observar esta relación: para gl=30, los valores t ya son muy parecidos a los valores z indicados en la parte de abajo de la tabla. Estos resultados tienen todo el sentido: cuantos más datos tienes, menor es el peaje que tienes que pagar (y, por supuesto, puedes utilizar una aplicación informática para calcular valores p más exactos para cualquier valor t que desees).

Qué hacer con valores t negativos

En el caso de la hipótesis alternativa “menor que” (H_a: xx < xx), tu estadístico de contraste sería un número negativo (situado a la izquierda del cero en la distribución t). En este caso, para obtener el valor p tienes que encontrar el porcentaje que queda por debajo, o a la izquierda, de tu estadístico de contraste. Sin embargo, la tabla t (incluida en el apéndice) no contiene estadísticos de contraste negativos.

Tranquilo, no hay de qué preocuparse. Debido a la simetría, el porcentaje que hay a la izquierda (debajo) de un valor t negativo es igual que el porcentaje que hay a la derecha (por encima) del valor t positivo. Por consiguiente, para determinar el valor p correspondiente a tu estadístico de contraste negativo, busca la versión positiva de tu estadístico de contraste en la tabla t, encuentra la probabilidad de cola derecha (“mayor que”) correspondiente y utiliza ese valor.

Por ejemplo, supongamos que el estadístico de contraste es –2,7105 con 9 grados de libertad y H_a es la alternativa “menor que”. Para determinar el valor p, primero buscas +2,7105 en la tabla t; según lo que hemos visto en el apartado anterior, sabes que su valor p está entre las cabeceras de columna 0,025 y 0,010. Como la distribución t es simétrica, el valor p para –2,7105 también está entre 0,025 y 0,010. De nuevo rechazas H₀ porque estos dos valores son menores o iguales que 0,05.

Analizar la alternativa “distinto de”

Para determinar el valor p cuando la hipótesis alternativa (H_a) es del tipo “distinto de”, sólo tienes que doblar (multiplicar por dos) la probabilidad que obtienes de la tabla t cuando buscas tu estadístico de contraste. ¿Por qué razón la doblas? Porque la tabla t únicamente muestra probabilidades del tipo “mayor que”, que sólo te cuentan la mitad de la película. Para encontrar el valor p cuando tienes una alternativa “distinto de”, debes sumar los valores p de las alternativas “menor que” y “mayor que”. Como la distribución t es simétrica, las probabilidades “menor que” y “mayor que” son idénticas, de manera que doblas la que has encontrado en la tabla t y ya tienes el valor p para la alternativa “distinto de”.

Por ejemplo, si el estadístico de contraste es 2,7171 y H_a es una alternativa del tipo “distinto de”, buscas 2,7171 en la tabla t (gl=9 otra vez) y compruebas que el valor p está entre 0,025 y 0,010, como hemos visto anteriormente. Éstos son los valores p para la alternativa “mayor que”. Ahora doblas esos valores para incluir la alternativa “menor que” y obtienes que el valor p para tu estadístico de contraste está entre 0,025 × 2=0,05 y 0,01 × 2=0,02.

Contrastar una proporción poblacional

Cuando la variable es categórica (por ejemplo el sexo de la persona, o si está a favor/en contra de una determinada cuestión) y únicamente se estudia una población o grupo (por ejemplo todos los votantes censados), para contrastar una afirmación referida a la proporción poblacional se utiliza el contraste de hipótesis descrito en este apartado. El contraste examina la proporción (p) de elementos de la población que poseen cierta característica, por ejemplo la proporción de personas que tienen teléfono móvil. La hipótesis nula es H₀: p = p₀, donde p₀ es cierto valor propuesto para la proporción poblacional, p. Por ejemplo, si la afirmación es que el 70% de las personas tienen teléfono móvil, p₀ es 0,70. La hipótesis alternativa es una de las siguientes: p>p₀, p<p₀, o p ≠ p₀. (En el capítulo 14 encontrarás más información sobre las hipótesis alternativas.)

La fórmula del estadístico de contraste para una única proporción (si se cumplen ciertas condiciones) es:

en la que es la proporción de elementos de la muestra que tienen esa característica, y z es un valor de la distribución Z (ver el capítulo 9). Para calcular el estadístico de contraste, haz lo siguiente:

1. Calcula la proporción muestral, , para lo cual tienes que coger el número de personas de la muestra que poseen la característica de interés (por ejemplo, el número de personas de la muestra que tienen teléfono móvil) y dividirlo por n, el tamaño muestral.

2. Calcula - p₀, donde p₀ es el valor indicado en H₀.

3. Calcula el error estándar, .

4. Divide el resultado del paso 2 por el resultado del paso 3.

Para interpretar tu estadístico de contraste, búscalo en la distribución normal estándar (distribución Z, incluida en el apéndice) y calcula el valor p. (En el capítulo 14 encontrarás más información sobre cómo calcular el valor p.)

Las condiciones para utilizar este estadístico de contraste son que np₀ ≥ 10 y n (1 – p₀) ≥ 10. (Hay más información en el capítulo 9.)

Por ejemplo, imagina que la marca Sincaries afirma que cuatro de cada cinco dentistas recomiendan la pasta de dientes Sincaries a sus pacientes. En este caso la población son todos los dentistas, y p es la proporción de ellos que recomiendan Sincaries. La afirmación es que p es igual a “cuatro de cada cinco”, es decir, p₀ es 4/5=0,8. Tú sospechas que la proporción es en realidad inferior a 0,8. Tus hipótesis son H₀ : p=0,8 contra H_a : p<0,8.

Supongamos que tomas una muestra de 200 pacientes odontológicos y 151 de ellos manifiestan que su dentista les ha recomendado la marca Sincaries. Para encontrar el estadístico de contraste para estos resultados, sigue los pasos siguientes:

1. Empieza con = 0,755 y n = 200.

2. Como p₀ = 0,8, restas 0,755 – 0,8 = –0,045 (el numerador del estadístico de contraste).

3. El error estándar es = 0,028 (el denominador del estadístico de contraste).

4. El estadístico de contraste es = –1,61.

Como el estadístico de contraste es negativo, significa que tus resultados muestrales están –1,61 errores estándares por debajo (menos que) del valor propuesto para la población. ¿Con qué frecuencia cabe esperar que se obtengan estos resultados si H₀ es verdadera? La probabilidad de alcanzar o superar –1,61 (en este caso, en sentido negativo) es 0,0537 (conserva el signo negativo y busca –1,61 en la tabla Z). Este resultado es tu valor p porque H_a es una hipótesis del tipo “menor que”. (En el capítulo 14 encontrarás más información al respecto.)

Como el valor p es mayor que 0,05 (aunque sea por poco), no tienes indicios suficientes para rechazar H₀. Concluyes que la afirmación de que el 80% de los dentistas recomiendan Sincaries no puede ser rechazada, de acuerdo con tus datos. No obstante, es importante comunicar también el valor p para que los demás puedan tomar sus propias decisiones.

La letra p se utiliza con dos significados distintos en este capítulo: valor p y p. La letra p por sí sola se refiere a la proporción poblacional, no al valor p. No te confundas. Cuando comuniques un valor p, asegúrate de poner delante la palabra “valor”, para que no se confunda con p, la proporción poblacional.

Comparar dos medias poblacionales (independientes)

Cuando la variable es numérica (por ejemplo ingresos, nivel de colesterol o kilómetros por litro de combustible) y se comparan dos poblaciones o grupos (por ejemplo hombres frente a mujeres), para contrastar una afirmación sobre la diferencia entre las medias de dichas poblaciones o grupos se utilizan los pasos descritos en este apartado (por ejemplo, ¿la diferencia entre las medias poblacionales es igual a cero, lo cual significa que las medias son idénticas?). A fin de recopilar los datos necesarios para este contraste es preciso seleccionar dos muestras aleatorias independientes (totalmente separadas), una de cada población.

La hipótesis nula es que las dos medias poblacionales son idénticas, o dicho de otro modo, que su diferencia es igual a cero. La notación de la hipótesis nula es H₀: μ₁ = μ₂, en la que μ₁ representa la media de la primera población y μ₂ representa la media de la segunda población.

También puedes expresar la hipótesis nula como H₀: μ₁ – μ₂ = 0, haciendo hincapié en que la diferencia es igual a cero si las medias son iguales.

La fórmula del estadístico de contraste para comparar dos medias (si se cumplen ciertas condiciones) es:

Para calcularla, haz lo siguiente:

1. Calcula las medias muestrales y (supondremos que nos dan las desviaciones estándares de las poblaciones, σ₁ y σ₂). n₁ y n₂ representan los dos tamaños muestrales (no es necesario que sean iguales).

Estos cálculos se explican en el capítulo 5.

2. Calcula la diferencia entre las dos medias muestrales: ₁ - ₂.

Como la diferencia μ₁–μ₂ es igual a cero si H₀ es verdadera, no es necesario incluirla en el numerador del estadístico de contraste. Sin embargo, si el valor de la diferencia es cualquier número distinto de cero, hay que restar ese valor en el numerador del estadístico de contraste.

3. Calcula el error estándar por medio de la siguiente ecuación:

4. Divide el resultado del paso 2 por el resultado del paso 3.

Para interpretar el estadístico de contraste, añade los dos pasos siguientes:

5. Busca tu estadístico de contraste en la distribución normal estándar (distribución Z) (encontrarás la tabla Z en el apéndice) y calcula el valor p.

(En el capítulo 14 encontrarás más información sobre cómo calcular el valor p.)

6. Compara el valor p con el nivel de significación, por ejemplo 0,05. Si es menor o igual que 0,05, rechazas H₀. De lo contrario no rechazas H₀.

(En el capítulo 14 encontrarás más información sobre los niveles de significación.)

Las condiciones para utilizar este contraste son, primero, que se conozcan las desviaciones estándares de las poblaciones, y segundo, que las dos poblaciones tengan una distribución normal o bien los dos tamaños muestrales sean suficientemente grandes para aplicar el teorema del límite central (lo tienes en el capítulo 11).

Por ejemplo, imagina que quieres comparar la absorción de dos marcas de papel de cocina (las llamaremos marca A y marca B). Puedes realizar esta comparación midiendo el número medio de gramos que puede absorber una hoja de cada marca antes de saturarse del todo. H₀ dice que la diferencia entre los promedios de absorción es cero (inexistente), y H_a dice que la diferencia no es cero. Dicho de otro modo, una marca es más absorbente que la otra. En notación estadística tenemos H₀ = μ₁ – μ₂ = 0 contra H_a = μ₁ – μ₂ ≠ 0. Aquí no se indica qué papel de cocina es más absorbente, de manera que hay que utilizar la alternativa “distinto de” (vuelve al capítulo 14 si lo necesitas).

Supongamos que seleccionas una muestra aleatoria de 50 hojas de cada marca y mides la absorción de cada una de ellas. Supongamos que la absorción media de la marca A (x₁) en tu muestra es 3 gramos, y supongamos que la desviación estándar de la población es 0,9 gramos. En el caso de la marca B (x₂), la absorción media es 3,5 gramos según los datos de tu muestra, y la desviación estándar de la población es 1,2 gramos. Realiza este contraste de hipótesis siguiendo los seis pasos anteriores:

1. Por la información que tienes, sabes que ₁ = 30, σ₁ = 9, ₂ = 35, σ₂ = 12, n₁ = 50 y n₂ = 50.

2. La diferencia entre las medias muestrales (marcas A–marca B) es = (30 – 35) = –5 gramos. (Una diferencia negativa simplemente significa que la media de la segunda muestra era más grande que la media de la primera.)

3. El error estándar es .

4. Al dividir la diferencia, –5, por el error estándar, 2,1213, te da –2,36. Éste es tu estadístico de contraste.

5. Para encontrar el valor p, busca –2,36 en la distribución normal estándar (distribución Z). Encontrarás la tabla Z en el apéndice. La probabilidad de superar –2,36, en este caso en sentido negativo, es igual a 0,0091. Como H_a es una alternativa del tipo “distinto de”, doblas este porcentaje, con lo que obtienes 2 × 0,0091 = 0,0182, tu valor p. (En el capítulo 14 encontrarás más información sobre la alternativa “distinto de”.)

6. Este valor p es bastante más pequeño que 0,05. Por consiguiente, tienes indicios suficientes para rechazar H₀.

Tu conclusión es que, por la información de tus muestras, existe una diferencia estadísticamente significativa entre la capacidad de absorción de estas dos marcas de papel de cocina. La marca B es más absorbente porque tiene una media más alta (que la media de la marca A menos la media de la marca B sea un número negativo significa que la marca B tenía un valor más alto).

Si una de las muestras, o las dos, tienen un tamaño inferior a 30, utilizas la distribución t (el valor correspondiente a los grados de libertad es n₁ – 1 o n₂ – 1, lo que sea más pequeño) para encontrar el valor p. Si las desviaciones estándares de las poblaciones, σ₁ y σ₂, se desconocen, utilizas en su lugar las desviaciones estándares de las muestras, s₁ y s₂, y utilizas la distribución t que tiene los grados de libertad arriba mencionados. (En el capítulo 10 encontrarás más información sobre la distribución t.)

Contraste de hipótesis para una diferencia media (prueba t para datos apareados)

Puedes realizar un contraste de hipótesis para una diferencia media utilizando la prueba descrita en este apartado cuando la variable es numérica (por ejemplo ingresos, nivel de colesterol o kilómetros por litro de combustible) y los elementos de la muestra están apareados de algún modo en relación con variables relevantes como por ejemplo la edad o el peso, o bien los mismos elementos se utilizan dos veces (por ejemplo, en una prueba preliminar y una prueba posterior). Las pruebas de datos apareados generalmente se utilizan para estudios en que alguien quiere saber si un nuevo tratamiento, técnica o método funciona mejor que otro método existente, sin tener que preocuparse de otros factores relacionados con los sujetos que puedan influir en los resultados. (Más información en el capítulo 17.)

La diferencia media (lo que se verifica en este apartado) no es lo mismo que la diferencia entre las medias (lo que se verificaba en el apartado anterior).

Por ejemplo, imagina que un investigador quiere averiguar si enseñar a los alumnos a leer utilizando un juego de ordenador da mejores resultados que enseñarles con un método fonético de eficacia probada. El investigador selecciona 20 alumnos y los organiza en 10 parejas en función de su dominio de la lectura, edad, coeficiente intelectual, etc. A continuación selecciona aleatoriamente a un alumno de cada pareja y le enseña a leer con el método informático (lo llamaremos MI), mientras que el otro aprende con el método fonético (lo llamaremos MF). Al final del estudio, los dos alumnos hacen el mismo examen de lectura. Los datos figuran en la tabla 15-1.

Los datos originales están en parejas, pero a ti únicamente te interesa la diferencia entre las puntuaciones obtenidas por los dos integrantes de cada pareja (la puntuación del alumno que ha aprendido con el método informático menos la puntuación del alumno que ha aprendido con el método fonético), no las puntuaciones en sí mismas. Por tanto, tu nuevo conjunto de datos son las diferencias apareadas (las diferencias entre las parejas de puntuaciones). Sus valores se indican en la última columna de la tabla 15-1.

Al examinar las diferencias entre las parejas de observaciones, en realidad tienes un solo conjunto de datos y un solo contraste de hipótesis para una media poblacional. En este caso la hipótesis nula es que la media (de las diferencias apareadas) es 0, y la hipótesis alternativa es que la media (de las diferencias apareadas) es>0. Si los dos métodos de aprendizaje son iguales, la media de las diferencias apareadas debe ser 0. Si el método informático es mejor, la media de las diferencias apareadas debe ser positiva (la puntuación de los alumnos que han aprendido con el método informático es mayor que la de los alumnos que han aprendido con el método fonético).

La notación de la hipótesis nula es H₀: σ_d = 0, donde σ_d es la media de las diferencias apareadas para la población (la d del subíndice simplemente te recuerda que estás trabajando con las diferencias apareadas).

La fórmula del estadístico de contraste para diferencias apareadas es , en la que es la media de todas las diferencias apareadas halladas en la muestra, y t_n–1 es un valor de la distribución t que tiene n_d –1 grados de libertad (puedes releer el capítulo 10).

Utilizas una distribución t porque en la mayoría de los experimentos con datos apareados el tamaño de muestra es pequeño o la desviación estándar de la población σ_d se desconoce, de manera que se estima con s_d. (En el capítulo 10 encontrarás más información sobre la distribución t.)

Para calcular el estadístico de contraste para diferencias apareadas, haz lo siguiente:

1. Para cada par de datos, coge el primer valor del par y réstale el segundo valor del par para encontrar la diferencia apareada. Considera que las diferencias son tu nuevo conjunto de datos.

2. Calcula la media, , y la desviación estándar, s_d, de todas las diferencias.

3. Siendo n_d el número de diferencias apareadas que tienes, calcula el error estándar:

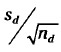
4. Divide por el error estándar calculado en el paso 3.

Como σ_d es igual a cero si H₀ es verdadera, no es necesario incluirla en la fórmula para hallar el estadístico de contraste. Por eso en ocasiones el estadístico de contraste se expresa de la manera siguiente:

En el ejemplo de las puntuaciones obtenidas en los exámenes de lectura, puedes utilizar los pasos anteriores para ver si el método informático es mejor para enseñar a leer a los alumnos.

Para encontrar el estadístico, sigue los pasos siguientes:

1. Calcula las diferencias para cada par (se indican en la columna 4 de la tabla 15-1).

El signo de cada diferencia es importante: indica qué método funcionó mejor para ese par en concreto.

2. Calcula la media y la desviación estándar de las diferencias calculadas en el paso 1.

Según mis cálculos, la media de las diferencias, , es igual a 2, y la desviación estándar, s_d, es igual a 4,64. Observa que aquí n_d = 10.

3. El error estándar es = 1,47.

(Recuerda que aquí n_d es el número de pares, que es 10.)

4. Si divides la media de las diferencias (paso 2) por el error estándar (paso 3) te sale 1,36, que es el estadístico de contraste.

¿El resultado del paso 4 es suficiente para decir que la diferencia entre puntuaciones hallada en este experimento se aplica a toda la población? Como la desviación estándar de la población, σ, se desconoce y la has estimado con la desviación estándar de la muestra (s), tienes que utilizar la distribución t en lugar de la distribución Z para encontrar el valor p. (Revisa el apartado “Muestras pequeñas y desviaciones estándares desconocidas: la prueba t”, en este mismo capítulo.) Para calcular el valor p, ve a la tabla t (incluida en el apéndice) y busca 1,36 en la distribución t que tiene 10–1=9 grados de libertad.

El valor p en este caso es mayor que 0,05 porque 1,36 es menor que el valor 1,38 de la tabla (es decir, se encuentra a la izquierda de dicho valor), y por tanto su valor p es mayor que 0,1 (el valor p para la cabecera de columna correspondiente a 1,38).

Como el valor p es mayor que 0,05, no rechazas H₀; no tienes indicios suficientes de que la diferencia media de puntuaciones entre el método informático y el método fonético sea significativamente mayor que cero.

Eso no significa necesariamente que no exista una diferencia real en la población formada por todos los alumnos. Sin embargo, el investigador no puede afirmar que el juego de ordenador es un método mejor basándose en esta muestra de 10 alumnos. (En el capítulo 14 encontrarás más información sobre la potencia de un contraste de hipótesis y su relación con el tamaño muestral.)

En muchos experimentos apareados, los conjuntos de datos son pequeños para reducir el coste económico del muestreo y el tiempo que requiere la realización de este tipo de estudios. Esto significa que generalmente se utiliza la distribución t (tienes la tabla t en el apéndice) en lugar de la distribución normal estándar (distribución Z, ver la tabla Z en el apéndice) para determinar el valor p.

Comparar dos proporciones poblacionales

Este contraste se utiliza cuando la variable es categórica (por ejemplo fumador/no fumador, demócrata/republicano, a favor/en contra de cierta opinión, etc.) y estás interesado en la proporción de personas que poseen una determinada característica, por ejemplo, la proporción de fumadores. En este caso se comparan dos poblaciones o grupos (por ejemplo, la proporción de mujeres fumadoras contra la de hombres fumadores).

Para realizar este contraste hay que seleccionar dos muestras aleatorias independientes (separadas), una de cada población. La hipótesis nula es que las dos proporciones poblacionales son idénticas, o dicho de otro modo, que su diferencia es igual a cero. La notación de la hipótesis nula es H₀: p₁ = p₂, donde p₁ es la proporción de la primera población y p₂ es la proporción de la segunda población.

Afirmar en H₀ que las dos proporciones son idénticas es lo mismo que decir que su diferencia es cero. Si empiezas con la ecuación p₁ = p₂ y restas p₂ en cada lado, te queda p₁ - p₂ = 0. Por lo tanto, puedes expresar la hipótesis nula de ambas formas.

La fórmula del estadístico de contraste para comparar dos proporciones (si se cumplen ciertas condiciones) es:

en la que ₁ es la proporción de elementos de la primera muestra que poseen la característica de interés, ₂ es la proporción de elementos de la segunda muestra que poseen la característica de interés, es la proporción de elementos de la muestra combinada (todos los elementos de la primera y la segunda muestra) que poseen la característica de interés, y z es un valor de la distribución Z (hablamos de ella en el capítulo 9). Para calcular el estadístico de contraste, haz lo siguiente:

1. Calcula las proporciones muestrales ₁ y ₂ para cada muestra. n₁ y n₂ representan los dos tamaños muestrales (no es necesario que sean iguales).

2. Calcula la diferencia entre las dos proporciones muestrales, ₁ - ₂.

3. Calcula la proporción muestral global , el número total de elementos de ambas muestras que poseen la característica de interés (por ejemplo, el número total de fumadores, ya sean hombres o mujeres, que hay en la muestra) dividido por el número total de elementos de ambas muestras (n₁ + n₂).

4. Calcula el error estándar:

5. Divide el resultado del paso 2 por el resultado del paso 4. La respuesta es tu estadístico de contraste.

Para interpretar el estadístico de contraste, búscalo en la distribución normal estándar (la tabla Z del apéndice), calcula el valor p y toma las decisiones que corresponda. (En el capítulo 14 encontrarás más información sobre valores p.)

Piensa ahora en los anuncios de medicamentos que salen en las revistas. La foto principal muestra un sol esplendoroso, campos de flores, gente sonriendo... todo el mundo es más feliz gracias a ese medicamento. La compañía farmacéutica afirma que sus medicamentos pueden reducir los síntomas de la alergia, ayudar a la gente a dormir mejor, bajar la tensión arterial o solucionar cualquier otro problema de salud. Quizá todo esto te parezca demasiado bueno para ser cierto, pero cuando pasas la página para ver el reverso del anuncio, te encuentras con la letra pequeña donde el laboratorio farmacéutico justifica sus afirmaciones (¡ahí es donde suelen estar las estadísticas!). En algún lugar de esa letra pequeña es probable que encuentres una tabla donde se indiquen los efectos adversos del medicamento en comparación con un grupo de control (sujetos que tomaron un medicamento ficticio), para establecer un parangón justo con los que realmente tomaron el medicamento (el grupo experimental; más información en el capítulo 17).

Si nos fijamos en la información de una combinación de anfetamina y dextroanfetamina indicada para el trastorno por déficit de atención e hiperactividad (TDAH), dice que 26 de los 374 sujetos (el 7%) a quienes se les administró el fármaco experimentaron vómitos como efecto secundario, frente a 8 de los 210 sujetos (el 4%) que tomaron un placebo. Ten presente que los pacientes no sabían qué tratamiento estaban recibiendo. De todas las personas de la muestra que tuvieron vómitos, los que tomaron el fármaco representaron un porcentaje más alto. Sin embargo, ¿es suficiente este porcentaje para afirmar que toda la población que lo tome tendrá vómitos? Puedes hacer un contraste de hipótesis para averiguarlo.

En este ejemplo tienes H₀: p₁ –p₂ =0 contra H_a: p₁ –p₂ >0, donde p₁ representa la proporción de sujetos que tuvieron vómitos al tomar el medicamento, y p₂ representa la proporción de sujetos que tuvieron vómitos tomando el placebo.

¿Por qué H_a contiene el signo > y no el signo <? H_a representa la situación en la que los sujetos que tomaron el fármaco tuvieron más vómitos que los que tomaron el placebo, algo que la FDA (y también cualquier candidato a tomar este medicamento) querría saber. En este sentido, el orden de los grupos también es importante. Te va mejor poner en primer lugar el grupo del fámaco, para que cuando calcules la proporción de sujetos que lo tomaron menos la proporción de sujetos que tomaron el placebo te salga un número positivo si H_a es verdadera. Si cambias los grupos de orden, el signo habría sido negativo.

Ahora calcula el estadístico de contraste:

1. En primer lugar, determinas que = 0,070 y = 0,038.

Los tamaños muestrales son n₁ =374 y n₂ =210, respectivamente.

2. La diferencia entre estas proporciones muestrales es ₁ - ₂ = 0,070 –0,038 =0,032.

3. La proporción muestral global es = 0,058.

4. El error estándar es =0,020.

5. Por último, el estadístico de contraste es 0,032/0,020=1,60. ¡Buf!

El valor p es la probabilidad de alcanzar o superar (en este caso en sentido positivo) 1,60. Esta probabilidad es 1–0,9452=0,0548. Este valor p es un poco mayor que 0,05, de manera que, técnicamente, no tienes indicios suficientes para rechazar H₀. Esto significa que, según tus datos, las personas que toman el fármaco no sufren más vómitos que aquellas que toman un placebo.

Una valor p muy próximo al mágico pero un tanto arbitrario nivel de significación de 0,05 es lo que en estadística se llama un resultado marginal. En el ejemplo anterior, como el valor p de 0,0548 está cerca de la frontera entre aceptar y rechazar H₀, generalmente se considera un resultado marginal y debe comunicarse como tal.

Lo bonito de dar a conocer un valor p es que eres tú quien toma la decisión final. Cuanto más pequeño es el valor p, más indicios tienes en contra de H₀, pero ¿cuándo puedes considerar que tienes suficientes indicios? Cada persona es diferente. Si te encuentras el informe de un estudio donde alguien haya encontrado un resultado estadísticamente significativo y ese resultado sea importante para ti, entérate de cuál era el valor p para poder tomar tu propia decisión. (Tienes más información en el capítulo 14.)