The Earth is orbiting around the Sun, which itself is orbiting around the center of the Milky Way. Our Milky Way, the Galaxy, is the only galaxy in which we are able to study astrophysical processes in detail. Therefore, our journey through extragalactic astronomy will begin in our home Galaxy, with which we first need to become familiar before we are ready to take off into the depths of the Universe. Knowing the properties of the Milky Way is indispensable for understanding other galaxies.

2.1 Galactic coordinates

On a clear night, and sufficiently far away from cities, one can see the magnificent band of the Milky Way on the sky (Fig. 2.1). This observation suggests that the distribution of light, i.e., that of the stars in the Galaxy is predominantly that of a thin disk, as is also clearly seen in Fig. 1.52. A detailed analysis of the geometry of the distribution of stars and gas confirms this impression. This geometry of the Galaxy suggests the introduction of two specially adapted coordinate systems which are particularly convenient for quantitative descriptions.

Spherical Galactic coordinates (ℓ,b). We consider a spherical coordinate system, with its center being “here”, at the location of the Sun (see Fig. 2.2). The Galactic plane is the plane of the Galactic disk, i.e., it is parallel to the band of the Milky Way. The two Galactic coordinates ℓ and b are angular coordinates on the sphere. Here, b denotes the Galactic latitude , the angular distance of a source from the Galactic plane, with $b \in [-90^{\circ },+90^{\circ }]$ . The great circle b = 0^∘ is then located in the plane of the Galactic disk. The direction b = 90^∘ is perpendicular to the disk and denotes the North Galactic Pole (NGP) , while $b = -90^{\circ }$ marks the direction to the South Galactic Pole (SGP). The second angular coordinate is the Galactic longitude ℓ, with ℓ ∈ [0^∘, 360^∘]. It measures the angular separation between the position of a source, projected perpendicularly onto the Galactic disk (see Fig. 2.2), and the Galactic center, which itself has angular coordinates b = 0^∘ and ℓ = 0^∘. Given ℓ and b for a source, its location on the sky is fully specified. In order to specify its three-dimensional location, the distance of that source from us is alsoneeded.

The conversion of the positions of sources given in Galactic coordinates (b, ℓ) to that in equatorial coordinates (α, δ) and vice versa is obtained from the rotation between these two coordinate systems, and is described by spherical trigonometry. ¹ The necessary formulae can be found in numerous standard texts. We will not reproduce them here, since nowadays this transformation is done nearly exclusively using computer programs. Instead, we will give some examples. The following figures refer to the Epoch 2000: due to the precession of the rotation axis of the Earth, the equatorial coordinate system changes with time, and is updated from time to time. The position of the Galactic center (at $\ell= 0^{\circ } = b$ ) is α = 17^h45. 6^m, $\delta = -28^{\circ }56.\!\!^{{\prime}}2$ in equatorial coordinates. This immediately implies that at the La Silla Observatory, located at geographic latitude − 29^∘, the Galactic center is found near the zenith at local midnight in May/June. Because of the high stellar density in the Galactic disk and the large extinction due to dust this is therefore not a good season for extragalactic observations from La Silla. The North Galactic Pole has coordinates $\alpha _{\mathrm{NGP}} = 192.85948^{\circ }\approx 12^{\mathrm{h}}51^{\mathrm{m}}$ , $\delta _{\mathrm{NGP}} = 27.12825^{\circ }\approx 27^{\circ }7.\!\!^{{\prime}}7$ .

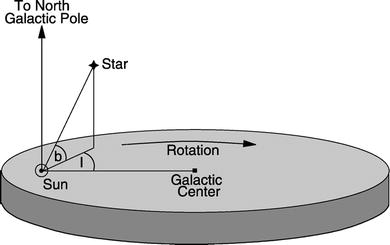
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig2_HTML.jpg

Fig. 2.2

The Sun is at the origin of the Galactic coordinate system. The directions to the Galactic center and to the North Galactic Pole (NGP) are indicated and are located at ℓ = 0^∘ and b = 0^∘, and at b = 90^∘, respectively. Adopted from: B.W. Carroll & D.A. Ostlie 1996, Introduction to Modern Astrophysics, Addison-Wesley

Zone of Avoidance.

As already mentioned, the absorption by dust and the presence of numerous bright stars render optical observations of extragalactic sources in the direction of the disk difficult. The best observing conditions are found at large | b | , while it is very hard to do extragalactic astronomy in the optical regime at | b | ≲ 10^∘; this region is therefore often called the ‘Zone of Avoidance’ . An illustrative example is the galaxy Dwingeloo 1, which was already mentioned in Sect. 1.1 (see Fig. 1.9). This galaxy was only discovered in the 1990s despite being in our immediate vicinity: it is located at low | b | , right in the Zone of Avoidance. As mentioned before, one of the prime motivations for carrying out the 2MASS survey (see Sect. 1.4) was to ‘peek’ through the dust in the Zone of Avoidance by observing in the near-IR bands.

Cylindrical Galactic coordinates (R, θ,z).

The angular coordinates introduced above are well suited to describing the angular position of a source relative to the Galactic disk. However, we will now introduce another three-dimensional coordinate system for the description of the Milky Way geometry that will prove very convenient in the study of its kinematic and dynamic properties. It is a cylindrical coordinate system, with the Galactic center at the origin (see also Fig. 2.22 below). The radial coordinate R measures the distance of an object from the Galactic center in the disk, and z specifies the height above the disk (objects with negative z are thus located below the Galactic disk, i.e., south of it). For instance, the Sun has a distance from the Galactic center of R = R ₀ ≈ 8 kpc. The angle θ specifies the angular separation of an object in the disk relative to the position of the Sun, as seen from the Galactic center. The distance of an object with coordinates R, θ, z from the Galactic center is then $\sqrt{R^{2 } + z^{2}}$ , independent of θ. If the matter distribution in the Milky Way was axially symmetric, the density would then depend only on R and z, but not on θ. Since this assumption is a good approximation, this coordinate system is very well suited for the physical description of the Galaxy.

2.2 Determination of distances within our Galaxy

A central problem in astronomy is the estimation of distances. The position of sources on the sphere gives us a two-dimensional picture. To obtain three-dimensional information, measurements of distances are required. We need to know the distance to a source if we want to draw conclusions about its physical parameters. For example, we can directly observe the angular diameter of an object, but to derive the physical size we need to know its distance. Another example is the determination of the luminosity L of a source, which can be derived from the observed flux S only by means of its distance D, using

$\displaystyle{ \fbox{$L = 4\pi S\,D^{2}.$} }$

(2.1)

It is useful to consider the dimensions of the physical parameters in this equation. The unit of the luminosity is $[L] = \mathrm{erg}\,\mathrm{s}^{-1}$ , and that of the flux $[S] = \mathrm{erg}\,\mathrm{s}^{-1}\,\mathrm{cm}^{-2}$ . The flux is the energy passing through a unit area per unit time (see Appendix A). Of course, the physical properties of a source are characterized by the luminosity L and not by the flux S, which depends on its distance from the Sun.

Here we will review various methods for the estimation of distances of objects in our Milky Way, postponing the discussion of methods for estimating extragalactic distances to Sect. 3.9.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig3_HTML.jpg

Fig. 2.3

Illustration of the parallax effect: in the course of the Earth’s orbit around the Sun the apparent positions of nearby stars on the sky seem to change relative to those of very distant background sources

2.2.1 Trigonometric parallax

The most important method of distance determination is the trigonometric parallax, not only from a historical point-of-view. This method is based on a purely geometric effect and is therefore independent of any physical assumptions. Due to the motion of the Earth around the Sun the positions of nearby stars on the sphere change relative to those of very distant sources (e.g., extragalactic objects such as quasars). The latter therefore define a fixed reference frame on the sphere (see Fig. 2.3). In the course of a year the apparent position of a nearby star follows an ellipse on the sphere, the semi-major axis of which is called the parallax p.² The axis ratio of this ellipse depends on the direction of the star relative to the ecliptic (the plane that is defined by the orbits of the Earth and the other planets) and is of no further interest here. The parallax depends on the radius r of the Earth’s orbit, hence on the Earth-Sun distance which is, by definition, one astronomical unit.³ Furthermore, the parallax depends on the distance D of the star,

$\displaystyle{ \frac{r} {D} =\tan p \approx p\;, }$

(2.2)

where we used p ≪ 1 in the last step, and p is measured in radians as usual. The trigonometric parallax is also used to define the common unit of distance in astronomy: one parsec (pc) is the distance of a hypothetical source for which the parallax is exactly p = 1″. With the conversion of arcseconds to radians (1″ ≈ 4. 848 × 10⁻⁶ radians) one gets $$p/1'' = 206265p$$

, which for a parsec yields

$\displaystyle{ \fbox{$1\mathrm{pc} = 206265\mathrm{AU} = 3.086 \times 10^{18}\mathrm{cm}$}\;. }$

(2.3)

The distance corresponding to a measured parallax is then calculated as

$\displaystyle{ \fbox{$D = \left (\frac{p} {1''}\right )^{-1}\mathrm{pc}$}\;. }$

(2.4)

To determine the parallax p, precise measurements of the position of an object at different times are needed, spread over a year, allowing us to measure the ellipse drawn on the sphere by the object’s apparent position. For ground-based observations the accuracy of this method is limited by the atmosphere. The seeing causes a blurring of the images of astronomical sources and thus limits the accuracy of position measurements. From the ground this method is therefore limited to parallaxes larger than ≈ 0. ^{′ ′} 01, implying that the trigonometric parallax yields distances to stars only within ∼ 30 pc.

An extension of this method towards smaller p, and thus larger distances, became possible with the astrometric satellite Hipparcos . It operated between November 1989 and March 1993 and measured the positions and trigonometric parallaxes of about 120 000 bright stars, with a precision of ∼ 0. ^{′ ′} 001 for the brighter targets. With Hipparcos the method of trigonometric parallax could be extended to stars up to distances of ∼ 300 pc. The satellite Gaia , the successor mission to Hipparcos, was launched on Dec. 19, 2013. Gaia will compile a catalog of ∼ 10⁹ stars up to V ≈ 20 in four broad-band and eleven narrow-band filters. It will measure parallaxes for these stars with an accuracy of ∼ 2 × 10⁻⁴ arcsec, and a considerably better accuracy for the brightest stars. Gaia will thus determine the distances for ∼ 2 × 10⁸ stars with a precision of 10 %, and tangential velocities (see next section) with a precision of better than 3 km∕s.

The trigonometric parallax method forms the basis of nearly all distance determinations owing to its purely geometrical nature. For example, using this method the distances to nearby stars have been determined, allowing the production of the Hertzsprung–Russell diagram (see Appendix B.2). Hence, all distance measures that are based on the properties of stars, such as will be described below, are calibrated by the trigonometric parallax.

2.2.2 Proper motions

Stars are moving relative to us or, more precisely, relative to the Sun. To study the kinematics of the Milky Way we need to be able to measure the velocities of stars. The radial component v _r of the velocity is easily obtained from the Doppler shift of spectral lines,

$\displaystyle{ \fbox{$v_{\mathrm{r}} = \frac{\varDelta \lambda } {\lambda _{0}}\,c$}\;, }$

(2.5)

where λ ₀ is the rest-frame wavelength of an atomic transition and $\varDelta \lambda =\lambda _{\mathrm{obs}} -\lambda _{0}$ the Doppler shift of the wavelength due to the radial velocity of the source. The sign of the radial velocity is defined such that v _r > 0 corresponds to a motion away from us, i.e., to a redshift of spectral lines.

In contrast, the determination of the other two velocity components is much more difficult. The tangential component, v _t, of the velocity can be obtained from the proper motion of an object. In addition to the motion caused by the parallax, stars also change their positions on the sphere as a function of time because of the transverse component of their velocity relative to the Sun. The proper motion μ is thus an angular velocity, e.g., measured in milliarcseconds per year (mas/yr). This angular velocity is linked to the tangential velocity component via

$\displaystyle{ \fbox{$v_{\mathrm{t}} = D\mu \mathrm{or} \frac{v_{\mathrm{t}}} {\mathrm{km/s}} = 4.74\left ( \frac{D} {1\,\mathrm{pc}}\right )\left ( \frac{\mu } {1''/\mathrm{yr}}\right )$}\;. }$

(2.6)

Therefore, one can calculate the tangential velocity from the proper motion and the distance. If the latter is derived from the trigonometric parallax, (2.6) and (2.4) can be combined to yield

$\displaystyle{ \frac{v_{\mathrm{t}}} {\mathrm{km/s}} = 4.74\left ( \frac{\mu } {1''/\mathrm{yr}}\right )\left (\frac{p} {1''}\right )^{-1}\;. }$

(2.7)

Hipparcos measured proper motions for ∼ 10⁵ stars with an accuracy of up to a few mas/yr; however, they can be translated into physical velocities only if their distance is known.

Of course, the proper motion has two components, corresponding to the absolute value of the angular velocity and its direction on the sphere. Together with v _r this determines the three-dimensional velocity vector. Correcting for the known velocity of the Earth around the Sun, one can then compute the velocity vector ${\boldsymbol v}$ of the star relative to the Sun, called the heliocentric velocity .

2.2.3 Moving cluster parallax

The stars in an (open) star cluster all have a very similar spatial velocity. This implies that their proper motion vectors should be similar. To what accuracy the proper motions are aligned depends on the angular extent of the star cluster on the sphere. Like two railway tracks that run parallel but do not appear parallel to us, the vectors of proper motions in a star cluster also do not appear parallel. They are directed towards a convergence point, as depicted in Fig. 2.4. We shall demonstrate next how to use this effect to determine the distance to a star cluster.

Fig. 2.4

The moving cluster parallax is a projection effect, similar to that known from viewing railway tracks. The directions of velocity vectors pointing away from us seem to converge and intersect at the convergence point. The connecting line from the observer to the convergence point is parallel to the velocity vector of the star cluster

We consider a star cluster and assume that all stars have the same spatial velocity ${\boldsymbol v}$ . The position of the i-th star as a function of time is then described by

$\displaystyle{ {\boldsymbol r}_{i}(t) ={\boldsymbol r}_{i} +{\boldsymbol v}t\;, }$

(2.8)

where ${\boldsymbol r}_{i}$ is the current position if we identify the origin of time, t = 0, with ‘today’. The direction of a star relative to us is described by the unit vector

$\displaystyle{ {\boldsymbol n}_{i}(t):= \frac{{\boldsymbol r}_{i}(t)} {\vert {\boldsymbol r}_{i}(t)\vert }\;. }$

(2.9)

From this, one infers that for large times, t → ∞, the direction vectors are identical for all stars in the cluster,

$\displaystyle{ {\boldsymbol n}_{i}(t) \rightarrow \frac{{\boldsymbol v}} {\vert {\boldsymbol v}\vert } =:{\boldsymbol n}_{\mathrm{conv}}\;. }$

(2.10)

Hence for large times all stars will appear at the same point ${\boldsymbol n}_{\mathrm{conv}}$ : the convergence point. This only depends on the direction of the velocity vector of the star cluster. In other words, the direction vector of the stars is such that they are all moving towards the convergence point. Thus, ${\boldsymbol n}_{\mathrm{conv}}$ (and hence ${\boldsymbol v}/\vert {\boldsymbol v}\vert$ ) can be measured from the direction of the proper motions of the stars in the cluster. On the other hand, one component of ${\boldsymbol v}$ can be determined from the (easily measured) radial velocity v _r. With these two observables the three-dimensional velocity vector ${\boldsymbol v}$ is completely determined, as is easily demonstrated: let ψ be the angle between the line-of-sight ${\boldsymbol n}$ towards a star in the cluster and ${\boldsymbol v}$ . The angle ψ is directly read off from the direction vector ${\boldsymbol n}$ and the convergence point, $\cos \psi ={\boldsymbol n} \cdot {\boldsymbol v}/\vert {\boldsymbol v}\vert ={\boldsymbol n}_{\mathrm{conv}} \cdot {\boldsymbol n}$ . With $v \equiv \vert {\boldsymbol v}\vert$ one then obtains

$\displaystyle{v_{\mathrm{r}} = v\cos \psi \quad,\quad v_{\mathrm{t}} = v\sin \psi \;,}$

and so

$\displaystyle{ v_{\mathrm{t}} = v_{\mathrm{r}}\tan \psi \;. }$

(2.11)

This means that the tangential velocity v _t can be measured without determining the distance to the stars in the cluster. On the other hand, (2.6) defines a relation between the proper motion, the distance, and v _t. Hence, a distance determination for the star is now possible with

$\displaystyle{ \mu = \frac{v_{\mathrm{t}}} {D} = \frac{v_{\mathrm{r}}\tan \psi } {D}\quad \rightarrow \quad D = \frac{v_{\mathrm{r}}\tan \psi } {\mu } \;. }$

(2.12)

This method yields accurate distance estimates of star clusters within ∼ 200 pc. The accuracy depends on the measurability of the proper motions. Furthermore, the cluster should cover a sufficiently large area on the sky for the convergence point to be well defined. For the distance estimate, one can then take the average over a large number of stars in the cluster if one assumes that the spatial extent of the cluster is much smaller than its distance to us. Targets for applying this method are the Hyades, a cluster of about 200 stars at a mean distance of D ≈ 45 pc, the Ursa-Major group of about 60 stars at D ≈ 24 pc, and the Pleiades with about 600 stars at D ≈ 130 pc.

Historically the distance determination to the Hyades, using the moving cluster parallax, was extremely important because it defined the scale to all other, larger distances. Its constituent stars of known distance are used to construct a calibrated Hertzsprung–Russell diagram which forms the basis for determining the distance to other star clusters, as will be discussed in Sect. 2.2.4. In other words, it is the lowest rung of the so-called distance ladder that we will discuss in Sect. 3.9. With Hipparcos, however, the distance to the Hyades stars could also be measured using the trigonometric parallax, yielding more accurate values. Hipparcos was even able to differentiate the ‘near’ from the ‘far’ side of the cluster—this star cluster is too close for the assumption of an approximately equal distance of all its stars to be still valid. A recent value for the mean distance of theHyades is

$\displaystyle{ \bar{D}_{\mathrm{Hyades}} = 46.3 \pm 0.3\mathrm{pc}\;. }$

(2.13)

2.2.4 Photometric distance; extinction and reddening

Most stars in the color-magnitude diagram are located along the main sequence. This enables us to compile a calibrated main sequence of those stars whose trigonometric parallaxes are measured, thus with known distances. Utilizing photometric methods, it is then possible to derive the distance to a star cluster, as we will demonstrate in the following.

The stars of a star cluster define their own main sequence (color-magnitude diagrams for some star clusters are displayed in Fig. 2.5); since they are all located at the same distance, their main sequence is already defined in a color-magnitude diagram in which only apparent magnitudes are plotted. This cluster main sequence can then be fitted to a calibrated main sequence⁴ by a suitable choice of the distance, i.e., by adjusting the distance modulus m − M,

$\displaystyle{m - M = 5\log (D/\mathrm{pc}) - 5\;,}$

where m and M denote the apparent and absolute magnitude, respectively.

Fig. 2.5

Color-magnitude diagram (CMD) for different star clusters. Such a diagram can be used for the distance determination of star clusters because the absolute magnitudes of main sequence stars are known (by calibration with nearby clusters, especially the Hyades). One can thus determine the distance modulus by vertically ‘shifting’ the main sequence. Also, the age of a star cluster can be estimated from a CMD: luminous main sequence stars have a shorter lifetime on the main sequence than less luminous ones. The turn-off point in the stellar sequence away from the main sequence therefore corresponds to that stellar mass for which the lifetime on the main sequence equals the age of the star cluster. Accordingly, the age is specified on the right axis as a function of the position of the turn-off point; the Sun will leave the main sequence after about 10 × 10⁹ yr. Credit: Allan Sandage, Carnegie

In reality this method cannot be applied so easily since the position of a star on the main sequence does not only depend on its mass but also on its age and metallicity. Furthermore, only stars of luminosity class V (i.e., dwarf stars) define the main sequence, but without spectroscopic data it is not possible to determine the luminosity class.

Extinction and reddening. Another major problem is extinction . Absorption and scattering of light by dust affect the relation of absolute to apparent magnitude: for a given M, the apparent magnitude m becomes larger (fainter) in the case of absorption, making the source appear dimmer. Also, since extinction depends on wavelength, the spectral energy distribution of the source is modified and the observed color of the star changes. Because extinction by dust is always associated with such a change in color, one can estimate the absorption—provided one has sufficient information on the intrinsic color of a source or of an ensemble of sources. We will now show how this method can be used to estimate the distance to a star cluster.

We consider the equation of radiative transfer for pure absorption or scattering (see Appendix A),

$\displaystyle{ \fbox{$\frac{\mathrm{d}I_{\nu }} {\mathrm{d}s} = -\kappa _{\nu }I_{\nu }$}\;, }$

(2.14)

where I _ν denotes the specific intensity at frequency ν, κ _ν the absorption coefficient, and s the distance coordinate along the light beam. The absorption coefficient has the dimension of an inverse length. Equation (2.14) says that the amount by which the intensity of a light beam is diminished on a path of length ds is proportional to the original intensity and to the path length ds. The absorption coefficient is thus defined as the constant of proportionality. In other words, on the distance interval ds, a fraction κ _ν ds of all photons at frequency ν is absorbed or scattered out of the beam. The solution of the transport equation (2.14) is obtained by writing it in the form $\mathrm{d}\ln I_{\nu } = \mathrm{d}I_{\nu }/I_{\nu } = -\kappa _{\nu }\,\mathrm{d}s$ and integrating from 0 to s,

$\displaystyle{\ln I_{\nu }(s) -\ln I_{\nu }(0) = -\int _{0}^{s}\mathrm{d}s'\;\kappa _{\nu }(s') \equiv -\tau _{\nu }(s)\;,}$

where in the last step we defined the optical depth , τ _ν , which depends on frequency. This yields

$\displaystyle{ \fbox{$I_{\nu }(s) = I_{\nu }(0)\,\mathrm{e}^{-\tau _{\nu }(s)}$}\;. }$

(2.15)

The specific intensity is thus reduced by a factor e^−τ compared to the case of no absorption taking place. Accordingly, for the flux we obtain

$\displaystyle{ \fbox{$S_{\nu } = S_{\nu }(0)\,\mathrm{e}^{-\tau _{\nu }(s)}$}\;, }$

(2.16)

where S _ν is the flux measured by the observer at a distance s from the source, and S _ν (0) is the flux of the source without absorption. Because of the relation between flux and magnitude $m = -2.5\,\log S + \mathrm{const.}$ , or S ∝ 10^−0. 4m , one has

$\displaystyle{ \frac{S_{\nu }} {S_{\nu,0}} = 10^{-0.4(m-m_{0})} = \mathrm{e}^{-\tau _{\nu }} = 10^{-\log (\mathrm{e})\tau _{\nu }}\;,}$

$\displaystyle\begin{array}{rcl} A_{\nu }&:=& m - m_{0} = -2.5\,\log (S_{\nu }/S_{\nu,0}) \\ & =& 2.5\,\log (\mathrm{e})\,\tau _{\nu } = 1.086\tau _{\nu }\;. {}\end{array}$

(2.17)

Here, A _ν is the extinction coefficient describing the change of apparent magnitude m compared to that without absorption, m ₀. Since the absorption coefficient κ _ν depends on frequency, absorption is always linked to a change in color. This is described by the color excess which is defined as follows:

$\displaystyle\begin{array}{rcl} E(X - Y )&:=& A_{X} - A_{Y } = (X - X_{0}) - (Y - Y _{0}) \\ & =& (X - Y ) - (X - Y )_{0}. {}\end{array}$

(2.18)

The color excess describes the change of the color index (X − Y ), measured in two filters X and Y that define the corresponding spectral windows by their transmission curves. The ratio $A_{X}/A_{Y } =\tau _{\nu (X)}/\tau _{\nu (Y )}$ depends only on the optical properties of the dust or, more specifically, on the ratio of the absorption coefficients in the two frequency bands X and Y considered here. Thus, the color excess is proportional to the extinction coefficient,

$\displaystyle\begin{array}{rcl} \fbox{$E(X - Y ) = A_{X} - A_{Y } = A_{X}\left (1 -\frac{A_{Y }} {A_{X}}\right ) \equiv A_{X}\,R_{X}^{-1}$}\;,& &{}\end{array}$

(2.19)

where in the last step we introduced the factor of proportionality R _X between the extinction coefficient and the color excess, which depends only on the properties of the dust and the choice of the filters. Usually, one considers a blue and a visual filter (see Appendix A.4.2 for a description of the filters commonly used) and writes

$\displaystyle{ A_{V } = R_{V }\,E(B - V )\;. }$

(2.20)

For example, for dust in our Milky Way we have the characteristic relation

$\displaystyle{ \fbox{$A_{V } = (3.1 \pm 0.1)E(B - V )$}\;. }$

(2.21)

Fig. 2.6

Wavelength dependence of the extinction coefficient A _ν , normalized to the extinction coefficient A _I at $\lambda = 9000\,\mathrm{{\AA}} = 0.9\,\upmu \mathrm{m}$ . Different kinds of clouds, characterized by the value of R _V , i.e., by the reddening law, are shown. On the x-axis the inverse wavelength is plotted, so that the frequency increases to the right. The solid curve specifies the mean Galactic extinction curve. The extinction coefficient, as determined from the observation of an individual star, is also shown; clearly the observed law deviates from the model in some details. The figure insert shows a detailed plot at relatively large wavelengths in the NIR range of the spectrum; at these wavelengths the extinction depends only weakly on the value of R _V . Source: B. Draine 2003, Interstellar Dust Grains, ARA&A 41, 241. Reprinted, with permission, from the Annual Review of Astronomy & Astrophysics, Volume 41 ©2003 by Annual Reviews www.annualreviews.org

This relation is not a universal law, but the factor of proportionality depends on the properties of the dust. They are determined, e.g., by the chemical composition and the size distribution of the dust grains. Figure 2.6 shows the wavelength dependence of the extinction coefficient for different kinds of dust, corresponding to different values of R _V . In the optical part of the spectrum we have approximately τ _ν ∝ ν, i.e., blue light is absorbed (or scattered) more strongly than red light. The extinction therefore always causes a reddening.⁵

Fig. 2.7

The column density of neutral hydrogen along the line-of-sight to Galactic stars, plotted as a function of the corresponding color excess E(B − V ), as shown by the points. The dashed line is the best-fitting linear relation as given by (2.22). The other symbols correspond to measurements of both quantities in distant galaxies and will be discussed in Sect. 3.11.4. Source: X. Dai & C.S. Kochanek 2009, Differential X-Ray Absorption and Dust-to-Gas Ratios of the Lens Galaxies SBS 0909+523, FBQS 0951+2635, and B 1152+199, ApJ 692, 677, p. 682, Fig. 5. ©AAS. Reproduced with permission

The extinction coefficient A _V is proportional to the optical depth towards a source, see (2.17), and according to (2.21), so is the color excess. Since the extinction is due to dust along the line-of-sight, the color excess is proportional to the column density of dust towards the source. If we assume that the dust-to-gas ratio in the interstellar medium does not vary greatly, we expect that the column density of neutral hydrogen N _H is proportional to the color excess. The former can be measured from the Lyman-α absorption in the spectra of stars, whereas the latter is obtained by comparing the observed color of these stars with the color expected for the type of star, given its spectrum (and thus, its spectral classification). One finds indeed that the color excess is proportional to the Hi column density (see Fig. 2.7), with

$\displaystyle{ E(B - V ) = 1.7\,\mathrm{mag}\left ( \frac{N_{\mathrm{H}}} {10^{22}\,\mathrm{atoms\,cm^{-2}}}\right )\;, }$

(2.22)

and a scatter of about 30 % around this relation. The fact that this scatter is so small indicates that the assumption of a constant dust-to-gas ratio is reasonable.

In the Solar neighborhood the extinction coefficient for sources in the disk is about

$\displaystyle{ A_{V } \approx 1\mathrm{mag}\, \frac{D} {1\mathrm{kpc}}\;, }$

(2.23)

but this relation is at best a rough approximation, since the absorption coefficient can show strong local deviations from this law, for instance in the direction of molecular clouds (see, e.g., Fig. 2.8).

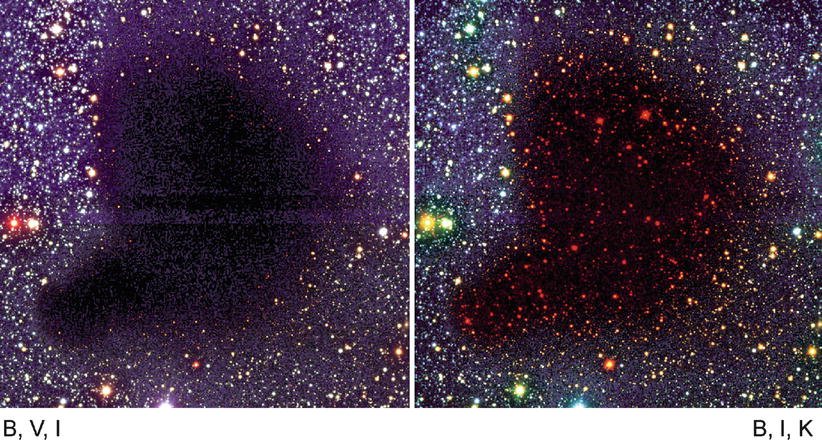
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig8_HTML.jpg

Fig. 2.8

These images of the molecular cloud Barnard 68 show the effects of extinction and reddening: the left image is a composite of exposures in the filters B, V, and I. At the center of the cloud essentially all the light from the background stars is absorbed. Near the edge it is dimmed and visibly shifted to the red. In the right-hand image observations in the filters B, I, and K have been combined (red is assigned here to the near-infrared K-band filter); we can clearly see that the cloud is more transparent at longer wavelengths. Credit: European Southern Observatory

Color-color diagram.

We now return to the distance determination for a star cluster. As a first step in this measurement, it is necessary to determine the degree of extinction, which can only be done by analyzing the reddening. The stars of the cluster are plotted in a color-color diagram, for example by plotting the colors (U − B) and (B − V ) on the two axes (see Fig. 2.9). A color-color diagram also shows a main sequence along which the majority of the stars are aligned. The wavelength-dependent extinction causes a reddening in both colors. This shifts the positions of the stars in the diagram. The direction of the reddening vector depends only on the properties of the dust and is here assumed to be known, whereas the amplitude of the shift depends on the extinction coefficient. In a similar way to the CMD, this amplitude can now be determined if one has access to a calibrated, unreddened main sequence for the color-color diagram which can be obtained from the examination of nearby stars. From the relative shift of the main sequence in the two diagrams one can then derive the reddening and thus the extinction. The essential point here is the fact that the color-color diagram is independent of the distance.

Fig. 2.9

Color-color diagram for main sequence stars. Spectral types and absolute magnitudes are specified along the lower curve. The upper curve shows the location of black bodies in the color-color diagram, with the temperature in units of 10³ K labeled along the curve. Interstellar reddening shifts the measured stellar locations parallel to the reddening vector indicated by the arrow. Source: A. Unsöld & B. Baschek, The New Cosmos, Springer-Verlag

This then defines the procedure for the distance determination of a star cluster using photometry: in the first step we determine the reddening E(B − V ), and thus with (2.21) also A _V , by shifting the main sequence in a color-color diagram along the reddening vector until it matches a calibrated main sequence. In the second step the distance modulus is determined by vertically (i.e., in the direction of M) shifting the main sequence in the color-magnitude diagram until it matches a calibrated main sequence. From this, the distance is finally obtained according to

$\displaystyle{ \fbox{$m - M = 5\log (D/1\mathrm{pc}) - 5 + A$}\;. }$

(2.24)

2.2.5 Spectroscopic distance

From the spectrum of a star, the spectral type as well as its luminosity class can be obtained. The former is determined from the strength of various absorption lines in the spectrum, while the latter is obtained from the width of the lines. From the line width the surface gravity of the star can be derived, and from that its radius (more precisely, M∕R ²). The spectral type and the luminosity class specify the position of the star in the HRD unambiguously. By means of stellar evolution models, the absolute magnitude M _V can then be determined. Furthermore, the comparison of the observed color with that expected from theory yields the color excess E(B − V ), and from that we obtain A _V . With this information we are then able to determine the distance using

$\displaystyle{ \fbox{$m_{V } - A_{V } - M_{V } = 5\log (D/\mathrm{pc}) - 5$}\;. }$

(2.25)

2.2.6 Distances of visual binary stars

Kepler’s third law for a two-body problem,

$\displaystyle{ \fbox{$P^{2} = \frac{4\pi ^{2}} {G(m_{1} + m_{2})}a^{3}$}\;, }$

(2.26)

relates the orbital period P of a binary star to the masses m _i of the two components and the semi-major axis a of the ellipse. The latter is defined by the separation vector between the two stars in the course of one period. This law can be used to determine the distance to a visual binary star. For such a system, the period P and the angular diameter 2θ of the orbit are direct observables. If one additionally knows the mass of the two stars, for instance from their spectral classification, a can be determined according to (2.26), and from this the distance follows with $D = a/\theta$ .

2.2.7 Distances of pulsating stars

Several types of pulsating stars show periodic changes in their brightnesses, where the period of a star is related to its mass, and thus to its luminosity. This period-luminosity (PL) relation is ideally suited for distance measurements: since the determination of the period is independent of distance, one can obtain the luminosity directly from the period if the calibrated PL-relation is known. The distance is thus directly derived from the measured magnitude using (2.25), if the extinction can be determined from color measurements.

The existence of a relation between the luminosity and the pulsation period can be expected from simple physical considerations. Pulsations are essentially radial density waves inside a star that propagate with the speed of sound, c _s. Thus, one can expect that the period is comparable to the sound crossing time through the star, P ∼ R∕c _s. The speed of sound c _s in a gas is of the same order of magnitude as the thermal velocity of the gas particles, so that $k_{\mathrm{B}}T \sim m_{\mathrm{p}}c_{\mathrm{s}}^{2}$ , where m _p is the proton mass (and thus a characteristic mass of particles in the stellar plasma) and k _B is Boltzmann’s constant. According to the virial theorem, one expects that the gravitational binding energy of the star is about twice the kinetic (i.e., thermal) energy, so that for a proton

$\displaystyle{\frac{GMm_{\mathrm{p}}} {R} \sim k_{\mathrm{B}}T\;.}$

Combining these relations, we obtain for the pulsation period

$\displaystyle{ P \sim \frac{R} {c_{\mathrm{s}}} \sim \frac{R\sqrt{m_{\mathrm{p}}}} {\sqrt{k_{\mathrm{B} } T}} \sim \frac{R^{3/2}} {\sqrt{GM}} \propto \bar{\rho }^{-1/2}\;, }$

(2.27)

where $\bar{\rho }$ is the mean density of the star. This is a remarkable result—the pulsation period depends only on the mean density. Furthermore, the stellar luminosity is related to its mass by approximately L ∝ M ³. If we now consider stars of equal effective temperature T _eff (where $L \propto R^{2}T_{\mathrm{eff}}^{4}$ ), we find that

$\displaystyle{ P \propto \frac{R^{3/2}} {\sqrt{M}} \propto L^{7/12}\;, }$

(2.28)

which is the relation between period and luminosity that we were aiming for.

Fig. 2.10

Period-luminosity relation for Galactic Cepheids, measured in three different filters bands (B, V, and I, from top to bottom). The absolute magnitudes were corrected for extinction by using colors. The period is given in days. Open and solid circles denote data for those Cepheids for which distances were estimated using different methods; the three objects marked by triangles have a variable period and are discarded in the derivation of the period-luminosity relation. The latter is indicated by the solid line, with its parametrization specified in the plots. The broken lines indicate the uncertainty range of the period-luminosity relation. The slope of the period-luminosity relation increases, and the dispersion of the individual measurements around the mean PL-relation decreases, if one moves to redder filters. Source: G.A. Tammann et al. 2003, New Period-Luminosity and Period-Color relations of classical Cepheids: I. Cepheids in the Galaxy, A&A 404, 423, p. 436, Fig. 11. ©ESO. Reproduced with permission

One finds that a well-defined period-luminosity relation exists for three types of pulsating stars:

δ Cepheid stars (classical Cepheids). These are young stars found in the disk population (close to the Galactic plane) and in young star clusters. Owing to their position in or near the disk, extinction always plays a role in the determination of their luminosity. To minimize the effect of extinction it is particularly useful to look at the period-luminosity relation in the near-IR (e.g., in the K-band at λ ∼ 2. 4 μm). Furthermore, the scatter around the period-luminosity relation is smaller for longer wavelengths of the applied filter, as is also shown in Fig. 2.10. The period-luminosity relation is also steeper for longer wavelengths, resulting in a more accurate determination of the absolute magnitude.
W Virginis stars, also called population II Cepheids (we will explain the term of stellar populations in Sect. 2.3.2). These are low-mass, metal-poor stars located in the halo of the Galaxy, in globular clusters, and near the Galactic center.
RR Lyrae stars. These are likewise population II stars and thus metal-poor. They are found in the halo, in globular clusters, and in the Galactic bulge. Their absolute magnitudes are confined to a narrow interval, M _V ∈ [0. 5, 1. 0], with a mean value of about 0.6. This obviously makes them very good distance indicators. More precise predictions of their magnitudes are possible with the following dependence on metallicity and period :

$\displaystyle\begin{array}{rcl} &&\left \langle M_{K}\right \rangle = -(2.0 \pm 0.3)\log (P/1\mathrm{d})\,+\,(0.06\,\pm \,0.04)[\mathrm{Fe/H}] \\ &&\quad\qquad\quad- 0.7 \pm 0.1\;. {}\end{array}$

(2.29)

Metallicity. In the last equation, the metallicity of a star was introduced, which needs to be defined. In astrophysics, all chemical elements heavier than helium are called metals. These elements, with the exception of some traces of lithium, were not produced in the early Universe but rather later in the interior of stars. The metallicity is thus also a measure of the chemical evolution and enrichment of matter in a star or gas cloud. For an element X, the metallicity index of a star is defined as

$\displaystyle\begin{array}{rcl} \fbox{$[\mathrm{X}/\mathrm{H}] \equiv \log \left (\frac{n(\mathrm{X})} {n(\mathrm{H})}\right )_{{\ast}}-\log \left (\frac{n(\mathrm{X})} {n(\mathrm{H})}\right )_{\odot }$}\;,& &{}\end{array}$

(2.30)

thus it is the logarithm of the ratio of the fraction of X relative to hydrogen in the star and in the Sun, where n is the number density of the species considered. For example, $[\mathrm{Fe}/\mathrm{H}] = -1$ means that iron has only a tenth of its Solar abundance. The metallicity Z is the total mass fraction of all elements heavier than helium; the Sun has Z ≈ 0. 02, meaning that about 98 % of the Solar mass is composed of hydrogen and helium.

The period-luminosity relations are not only of significant importance for distance determinations within our Galaxy. They also play an essential role in extragalactic astronomy, since the Cepheids (which are by far the most luminous of the three types of pulsating stars listed above) are also found and observed outside the Milky Way; they therefore enable us to directly determine the distances of other galaxies, which is essential for measuring the Hubble constant. These aspects will be discussed in detail in Sect. 3.9.

2.3 The structure of the Galaxy

Roughly speaking, the Galaxy consists of the disk, the central bulge, and the Galactic halo—a roughly spherical distribution of stars and globular clusters that surrounds the disk. The disk, whose stars form the visible band of the Milky Way, contains spiral arms similar to those observed in other spiral galaxies. The Sun, together with its planets, orbits around the Galactic center on an approximately circular orbit. The distance R ₀ to the Galactic center is not very accurately known, as we will discuss later. To have a reference value, the International Astronomical Union (IAU) officially defined the value of R ₀ in 1985,

$\displaystyle\begin{array}{rcl} \fbox{$R_{0} = 8.5\,\mathrm{kpc}$}\quad \mbox{ official value, IAU 1985}\;.& &{}\end{array}$

(2.31)

More recent examinations have, however, found that the real value is slightly smaller, R ₀ ≈ 8. 0 kpc. The diameter of the disk of stars, gas, and dust is ∼ 50 kpc. A schematic depiction of our Galaxy is shown in Fig. 1.6.

2.3.1 The Galactic disk: Distribution of stars

By measuring the distances of stars in the Solar neighborhood one can determine the three-dimensional stellar distribution. From these investigations, one finds that there are different stellar components, as we will discuss below. For each of them, the number density in the direction perpendicular to the Galactic disk is approximately described by an exponential law,

$\displaystyle{ n(z) \propto \exp \left (-\frac{\vert z\vert } {h} \right )\;, }$

(2.32)

where the scale-height h specifies the thickness of the respective component. One finds that h varies between different populations of stars, motivating the definition of different components of the Galactic disk. In principle, three components need to be distinguished: (1) The young thin disk contains the largest fraction of gas and dust in the Galaxy, and in this region star formation is still taking place today. The youngest stars are found in the young thin disk, which has a scale-height of about h _ytd ∼ 100 pc. (2) The old thin disk is thicker and has a scale-height of about h _otd ∼ 325 pc. (3) The thick disk has a scale-height of h _thick ∼ 1. 5 kpc. The thick disk contributes only about 2 % to the total mass density in the Galactic plane at z = 0. This separation into three disk components is rather coarse and can be further refined if one uses a finer classification of stellar populations.

Molecular gas, out of which new stars are born, has the smallest scale-height, h _mol ∼ 65 pc, followed by the atomic gas. This can be clearly seen by comparing the distributions of atomic and molecular hydrogen in Fig. 1.8. The younger a stellar population is, the smaller its scale-height. Another characterization of the different stellar populations can be made with respect to the velocity dispersion of the stars, i.e., the amplitude of the components of their random motions. As a first approximation, the stars in the disk move around the Galactic center on circular orbits. However, these orbits are not perfectly circular: besides the orbital velocity (which is about 220 km∕s in the Solar vicinity), they have additional random velocity components.

Velocity dispersion. The formal definition of the components of the velocity dispersion is as follows: let $f({\boldsymbol v})\,\mathrm{d}^{3}v$ be the number density of stars (of a given population) at a fixed location, with velocities in a volume element d³ v around ${\boldsymbol v}$ in the vector space of velocities. If we use Cartesian coordinates, for example ${\boldsymbol v} = (v_{1},v_{2},v_{3})$ , then $f({\boldsymbol v})\,\mathrm{d}^{3}v$ is the number of stars with the i-th velocity component in the interval $[v_{i},v_{i} + \mathrm{d}v_{i}]$ , and $\mathrm{d}^{3}v = \mathrm{d}v_{1}\,\mathrm{d}v_{2}\,\mathrm{d}v_{3}$ . The mean velocity $\left \langle {\boldsymbol v}\right \rangle$ of the population then follows from this distribution via

$\displaystyle{ \left \langle {\boldsymbol v}\right \rangle = n^{-1}\,\int _{ \mathrm{IR}^{3}}\mathrm{d}^{3}v\;f({\boldsymbol v})\,{\boldsymbol v}\;,\;\;\mathrm{where}\;\;n =\int _{\mathrm{ IR}^{3}}\mathrm{d}^{3}v\;f({\boldsymbol v}) }$

(2.33)

denotes the total number density of stars in the population. The velocity dispersion σ then describes the root mean square deviations of the velocities from $\left \langle {\boldsymbol v}\right \rangle$ . For a component i of the velocity vector, the dispersion σ _i is defined as

$\displaystyle\begin{array}{rcl} \sigma _{i}^{2} = \left \langle \left (v_{ i} -\left \langle v_{i}\right \rangle \right )^{2}\right \rangle = \left \langle v_{ i}^{2} -\left \langle v_{ i}\right \rangle ^{2}\right \rangle = n^{-1}\,\int _{ \mathrm{IR}^{3}}\mathrm{d}^{3}v\;f({\boldsymbol v})\,\left (v_{ i}^{2} -\left \langle v_{ i}\right \rangle ^{2}\right )\;.& &{}\end{array}$

(2.34)

The larger σ _i is, the broader the distribution of the stochastic motions. We note that the same concept applies to the velocity distribution of molecules in a gas. The mean velocity $\left \langle {\boldsymbol v}\right \rangle$ at each point defines the bulk velocity of the gas, e.g., the wind speed in the atmosphere, whereas the velocity dispersion is caused by thermal motion of the molecules and is determined by the temperature of the gas.

The random motion of the stars in the direction perpendicular to the disk is the reason for the finite thickness of the population; it is similar to a thermal distribution. Accordingly, it has the effect of a pressure, the so-called dynamical pressure of the distribution. This pressure determines the scale-height of the distribution, which corresponds to the law of atmospheres. The larger the dynamical pressure, i.e., the larger the velocity dispersion σ _z perpendicular to the disk, the larger the scale-height h will be. The analysis of stars in the Solar neighborhood yields σ _z ∼ 16 km∕s for stars younger than ∼ 3 Gyr, corresponding to a scale-height of h ∼ 250 pc, whereas stars older than ∼ 6 Gyr have a scale-height of ∼ 350 pc and a velocity dispersion of σ _z ∼ 25 km∕s.

The density distribution of the total star population, obtained from counts and distance determinations of stars, is to a good approximation described by

$\displaystyle\begin{array}{rcl} \fbox{$n(R,z) = n_{0}\left (\mathrm{e}^{-\vert z\vert /h_{\mathrm{thin}} } + 0.02\mathrm{e}^{-\vert z\vert /h_{\mathrm{thick}} }\right )\mathrm{e}^{-R/h_{R} }$}\;;& &{}\end{array}$

(2.35)

here, R and z are the cylinder coordinates introduced above (see Sect. 2.1), with the origin at the Galactic center, and h _thin ≈ h _otd ≈ 325 pc is the scale-height of the thin disk. The distribution in the radial direction can also be well described by an exponential law, where h _R ≈ 3. 5 kpc denotes the scale-length of the Galactic disk. The normalization of the distribution is determined by the density n ≈ 0. 2 stars∕pc³ in the Solar neighborhood, for stars in the range of absolute magnitudes of 4. 5 ≤ M _V ≤ 9. 5. The distribution described by (2.35) is not smooth at z = 0; it has a kink at this point and it is therefore unphysical. To get a smooth distribution which follows the exponential law for large z and is smooth in the plane of the disk, the distribution is slightly modified. As an example, for the luminosity density of the old thin disk (that is proportional to the number density of the stars), we can write:

$\displaystyle{ \fbox{$L(R,z) = \frac{L_{0}\,\mathrm{e}^{-R/h_{R}}} {\cosh ^{2}(z/h_{z})} $}\;, }$

(2.36)

with $h_{z} = 2h_{\mathrm{thin}}$ and L ₀ ≈ 0. 05L _⊙∕pc³. The Sun is a member of the young thin disk and is located above the plane of the disk, at z ≈ 30 pc.

2.3.2 The Galactic disk: chemical composition and age; supernovae

Stellar populations. The chemical composition of stars in the thin and the thick disks differs: we observe the clear tendency that stars in the thin disk have a higher metallicity than those in the thick disk. In contrast, the metallicity of stars in the Galactic halo and in the bulge is smaller. To paraphrase these trends, one distinguishes between stars of population I (pop I) which have a Solar-like metallicity (Z ∼ 0. 02) and are mainly located in the thin disk, and stars of population II (pop II) that are metal-poor (Z ∼ 0. 001) and predominantly found in the thick disk, in the halo, and in the bulge. In reality, stars cover a wide range in Z, and the figures above are only characteristic values. For stellar populations a somewhat finer separation was also introduced, such as ‘extreme population I’, ‘intermediate population II’, and so on. The populations also differ in age (stars of pop I are younger than those of pop II), in scale height (as mentioned above), and in the velocity dispersion perpendicular to the disk (σ _z is larger for pop II stars than for pop I stars).

We shall now attempt to understand the origin of these different metallicities and their relation to the scale height and to age, starting with a brief discussion of the phenomenon that is the main reason for the metal enrichment of the interstellar medium.

Metallicity and supernovae. Supernovae (SNe) are explosive events. Within a few days, a SN can reach a luminosity of $10^{9}L_{\odot }$ , which is a considerable fraction of the total luminosity of a galaxy; after that the luminosity decreases again with a time-scale of weeks. In the explosion, a star is disrupted and (most of) the matter of the star is driven into the interstellar medium, enriching it with metals that were produced in the course of stellar evolution or in the process of the supernova explosion.

Classification of supernovae. Based on their spectral properties, SNe are divided into several classes. SNe of Type I do not show any Balmer lines of hydrogen in their spectrum, in contrast to those of Type II. The Type I SNe are further subdivided: SNe Ia show strong emission of Siii λ 6150 Å whereas no Siii at all is visible in spectra of Type Ib,c. Our current understanding of the supernova phenomenon differs from this spectral classification.⁶ Following various observational results and also theoretical analyses, we are confident today that SNe Ia are a phenomenon which is intrinsically different from the other supernova types. For this interpretation, it is of particular importance that SNe Ia are found in all types of galaxies, whereas we observe SNe II and SNe Ib,c only in spiral and irregular galaxies, and here only in those regions in which blue stars predominate. As we will see in Chap. 3, the stellar population in elliptical galaxies consists almost exclusively of old stars, while spirals also contain young stars. From this observational fact it is concluded that the phenomenon of SNe II and SNe Ib,c is linked to a young stellar population, whereas SNe Ia occur also in older stellar populations. We shall discuss the two classes of supernovae next.

Core-collapse supernovae. SNe II and SNe Ib,c are the final stages in the evolution of massive ( ≳ 8M _⊙) stars. Inside these stars, ever heavier elements are generated by nuclear fusion: once all the hydrogen in the inner region is used up, helium will be burned, then carbon, oxygen, etc. This chain comes to an end when the iron nucleus is reached, the atomic nucleus with the highest binding energy per nucleon. After this no more energy can be gained from fusion to heavier elements so that the pressure, which is normally balancing the gravitational force in the star, can no longer be maintained. The star then collapse under its own gravity. This gravitational collapse proceeds until the innermost region reaches a density about three times the density of an atomic nucleus. At this point the so-called rebounce occurs: a shock wave runs towards the surface, thereby heating the infalling material, and the star explodes. In the center, a compact object probably remains—a neutron star or, possibly, depending on the mass of the iron core, a black hole. Such neutron stars are visible as pulsars⁷ at the location of some historically observed SNe, the most famous of which is the Crab pulsar which has been identified with a supernovae explosion seen by Chinese astronomers in 1054. Presumably all neutron stars have been formed in such core-collapse supernovae.

Fig. 2.11

Chemical shell structure of a massive star at the end of its life with the axis labeled by the mass within a given radius. The elements that have been formed in the various stages of the nuclear burning are ordered in a structure resembling that of an onion, with heavier elements being located closer to the center. This is the initial condition for a supernova explosion. Adapted from A. Unsöld & B. Baschek, The New Cosmos, Springer-Verlag

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig12_HTML.jpg

Fig. 2.12

The relative abundance of chemical elements in the Solar System, normalized such that silicon attains the value 10⁶. By far the most abundant elements are hydrogen and helium; as we will see later, these elements were produced in the first 3 min of the cosmic evolution. Essentially all the other elements were produced later in stellar interiors. As a general trend, the abundances decrease with increasing atomic number, except for the light elements lithium (Li), beryllium (Be), and boron (B), which are generated in stars, but also easily destroyed due to their low binding energy. Superposed on this decrease, the abundances show an oscillating behavior: nuclei with an even number of protons are more abundant than those with an odd atomic number—this phenomenon is due to the production of alpha elements in core-collapse supernovae. Furthermore, iron (Fe), cobalt (Co) and nickel (Ni) stick out in their relatively high abundance, given their atomic number, which is due to their abundant production mainly in Type Ia SNe. Source: Wikipedia, numerical data from: Katharina Lodders

The major fraction of the binding energy released in the formation of the compact object is emitted in the form of neutrinos: about 3 × 10⁵³ erg. Underground neutrino detectors were able to trace about 10 neutrinos originating from SN 1987A in the Large Magellanic Cloud.⁸ Due to the high density inside the star after the collapse, even neutrinos, despite their very small cross section, are absorbed and scattered, so that part of their outward-directed momentum contributes to the explosion of the stellar envelope. This shell expands at v ∼ 10 000 km∕s, corresponding to a kinetic energy of E _kin ∼ 10⁵¹ erg. Of this, only about 10⁴⁹ erg is converted into photons in the hot envelope and then emitted—the energy of a SN that is visible in photons is thus only a small fraction of the total energy produced.

Owing to the various stages of nuclear fusion in the progenitor star, the chemical elements are arranged in shells: the light elements (H, He) in the outer shells, and the heavier elements (C, O, Ne, Mg, Si, Ar, Ca, Fe, Ni) in the inner ones—see Fig. 2.11. The explosion ejects them into the interstellar medium which is thus chemically enriched. It is important to note that mainly nuclei with an even number of protons and neutrons are formed. This is a consequence of the nuclear reaction chains involved, where successive nuclei in this chain are obtained by adding an α-particle (or⁴He-nucleus), i.e., two protons and two neutrons. Such elements are therefore called α-elements. The dominance of α-elements in the chemical abundance of the interstellar medium, as well as in the Solar System (see Fig. 2.12), is thus a clear indication of nuclear fusion occurring in the He-rich zones of stars where the hydrogen has been burnt.

Supernovae Type Ia.

SNe Ia are most likely the explosions of white dwarfs (WDs). These compact stars which form the final evolutionary stages of less massive stars no longer maintain their internal pressure by nuclear fusion. Rather, they are stabilized by the degeneracy pressure of the electrons—a quantum mechanical phenomenon related to the Fermi exclusion principle. Such a white dwarf can be stable only if its mass does not exceed a limiting mass, the Chandrasekhar mass; it has a value of $M_{\mathrm{Ch}} \approx 1.44M_{\odot }$ . For M > M _Ch, the degeneracy pressure can no longer balance the gravitational force.

A white dwarf can become unstable if its mass approaches the Chandrasekhar mass limit. There are two different scenarios with which this is possible: If the white dwarf is part of a close binary system, matter from the companion star may flow onto the white dwarf; this is called the ‘single-degenerate’ model. In this process, its mass will slowly increase and approach the limiting mass. At about M ≈ 1. 3M _⊙, carbon burning will ignite in its interior, transforming about half of the star into iron-group elements, i.e., iron, cobalt, and nickel. The resulting explosion of the star will enrich the ISM with ∼ 0. 6 M _⊙ of Fe, while the WD itself will be torn apart completely, leaving no remnant star. A second (so-called ‘double-degenerate’) scenario for the origin of SNe Ia is that of the merger of two white dwarfs for which the sum of their masses exceeds the Chandrasekhar mass. Of course, these two scenarios are not mutually exclusive, and both routes may be realized in nature.

Since the initial conditions are probably very homogeneous for the class of SNe Ia in the single-degenerate scenario (defined by the limiting mass prior to the trigger of the explosion), they are good candidates for standard candles: all SNe Ia have approximately the same luminosity. As we will discuss later (see Sect. 3.9.4), this is not really the case, but nevertheless SNe Ia play a very important role in the cosmological distance determination, and thus in the determination of cosmological parameters. On the other hand, in the double-degenerate scenario, the class of SNe Ia is not expected to be very homogeneous, as the mass prior to the explosion no longer attains a universal value. In fact, there are some SNe Ia which are clearly different from the majority of this class, by being far more luminous. It may be that such events are triggered by the merging of two white dwarfs, whereas the majority of the explosions is caused by the single-degenerate formation process.

This interpretation of the different types of SNe explains why one finds core-collapse SNe only in galaxies in which star formation occurs. They are the final stages of massive, i.e., young, stars which have a lifetime of not more than 2 × 10⁷ yr. By contrast, SNe Ia can occur in all types of galaxies, since their progenitors are members of an old stellar population.

In addition to SNe, metal enrichment of the interstellar medium (ISM) also takes place in other stages of stellar evolution, by stellar winds or during phases in which stars eject part of their envelope which is then visible, e.g., as a planetary nebula. If the matter in the star has been mixed by convection prior to such a phase, so that the metals newly formed by nuclear fusion in the interior have been transported towards the surface of the star, these metals will then be released into the ISM.

Age-metallicity relation. Assuming that at the beginning of its evolution the Milky Way had a chemical composition with only low metal content, the metallicity should be strongly related to the age of a stellar population. With each new generation of stars, more metals are produced and ejected into the ISM, partially by stellar winds, but mainly by SN explosions. Stars that are formed later should therefore have a higher metal content than those that were formed in the early phase of the Galaxy. One would thus expect that a relation exists between the age of a star and its metallicity.

For instance, under this assumption the iron abundance [Fe/H] can be used as an age indicator for a stellar population, with the iron predominantly being produced and ejected in SNe of Type Ia. Therefore, a newly formed generation of stars has a higher fraction of iron than their predecessors, and the youngest stars should have the highest iron abundance. Indeed one finds $[\mathrm{Fe}/\mathrm{H}] = -4.5$ (i.e., 3 × 10⁻⁵ of the Solar iron abundance) for extremely old stars, whereas very young stars have $[\mathrm{Fe}/\mathrm{H}] = 1$ , so their metallicity can significantly exceed that of the Sun.

However, this age-metallicity relation is not very tight. On the one hand, SNe Ia occur only ≳ 10⁹ yr after the formation of a stellar population. The exact time-span is not known because even if one accepts the accretion scenario for SN Ia described above, it is unclear in what form and in what systems the accretion of material onto the white dwarf takes place and how long it typically takes until the limiting mass is reached. On the other hand, the mixing of the SN ejecta in the ISM occurs only locally, so that large inhomogeneities of the [Fe/H] ratio may be present in the ISM, and thus even for stars of the same age. An alternative measure for metallicity is [O/H], because oxygen, which is an α-element, is produced and ejected mainly in supernova explosions of massive stars. These happen just ∼ 10⁷yr after the formation of a stellar population, which is virtually instantaneous.

Origin of the thick disk. Characteristic values for the metallicity are $-0.5 \lesssim [\mathrm{Fe/H}] \lesssim 0.3$ in the thin disk, while for the thick disk $-1.0 \lesssim [\mathrm{Fe/H}] \lesssim -0.4$ is typical. From this, one can deduce that stars in the thin disk must be significantly younger on average than those in the thick disk. This result can now be interpreted using the age-metallicity relation. Either star formation has started earlier, or ceased earlier, in the thick disk than in the thin disk, or stars that originally belonged to the thin disk have migrated into the thick disk. The second alternative is favored for various reasons. It would be hard to understand why molecular gas, out of which stars are formed, was much more broadly distributed in earlier times than it is today, where we find it well concentrated near the Galactic plane. In addition, the widening of an initially narrow stellar distribution in time is also expected. The matter distribution in the disk is not homogeneous and, along their orbits around the Galactic center, stars experience this inhomogeneous gravitational field caused by other stars, spiral arms, and massive molecular clouds. Stellar orbits are perturbed by such fluctuations, i.e., they gain a random velocity component perpendicular to the disk from local inhomogeneities of the gravitational field. In other words, the velocity dispersion σ _z of a stellar population grows in time, and the scale height of a population increases. In contrast to stars, the gas keeps its narrow distribution around the Galactic plane due to internal friction.

This interpretation is, however, not unambiguous. Another scenario for the formation of the thick disk is also possible, where the stars of the thick disk were formed outside the Milky Way and only became constituents of the disk later, through accretion of satellite galaxies. This model is supported, among other reasons, by the fact that the rotational velocity of the thick disk around the Galactic center is smaller by ∼ 50 km∕s than that of the thin disk. In other spirals, in which a thick disk component was found and kinematically analyzed, the discrepancy between the rotation curves of the thick and thin disks is sometimes even stronger. In one case, the thick disk was observed to rotate around the center of the galaxy in the opposite direction to the gas disk. In such a case, the aforementioned model of the evolution of the thick disk by kinematic heating of stars would definitely not apply.

Mass-to-light ratio. The total stellar mass of the thin disk is ∼ 6 × 10¹⁰ M _⊙, to which ∼ 0. 5 × 10¹⁰ M _⊙ in the form of dust and gas has to be added. The luminosity of the stars in the thin disk is $L_{B} \approx 1.8 \times 10^{10}L_{\odot }$ . Together, this yields a mass-to-light ratio of

$\displaystyle{ \fbox{$ \frac{M} {L_{B}} \approx 3\frac{M_{\odot }} {L_{\odot }} \mbox{ in thin disk}$}\;. }$

(2.37)

The M∕L ratio in the thick disk is higher, as expected from an older stellar population. The relative contribution of the thick disk to the stellar budget of the Milky Way is quite uncertain; estimates range from ∼ 5 to ∼ 30 %, which reflects the difficulty to attribute individual stars to the thin vs. thick disk; also the criteria for this classification vary substantially. In any case, due to the larger mass-to-light ratio of the thick disk, its contribution to the luminosity of the Milky Way is small. Nevertheless, the thick disk is invaluable for the diagnosis of the dynamical evolution of the disk. If the Milky Way were to be observed from the outside, one would find a M∕L value for the disk of about four in Solar units; this is a characteristic value for spiral galaxies.

2.3.3 The Galactic disk: dust and gas

Spatial distribution. The spiral structure of the Milky Way and other spiral galaxies is delineated by very young objects like O- and B-stars and Hii-regions.⁹ This is the reason why spiral arms appear blue. Obviously, star formation in our Milky Way takes place mainly in the spiral arms. Here, the molecular clouds —gas clouds which are sufficiently dense and cool for molecules to form in large abundance—contract under their own gravity and form new stars. The spiral arms are much less prominent in red light (see also Fig. 3.24 below). Emission in the red is dominated by an older stellar population, and these old stars have had time to move away from the spiral arms. The Sun is located close to, but not in, a spiral arm—the so-called Orion arm (see Fig. 2.13).

Open clusters. Star formation in molecular clouds leads to the formation of open star clusters, since stars are not born individually; instead, the contraction of a molecular cloud gives rise to many stars at the same time, which form an (open) star cluster. Its mass depends of course on the mass of the parent molecular cloud, ranging from ∼ 100 M _⊙ to $\sim 10^{4}\,M_{\odot }$ . The stars in these clusters all have the same velocity—indeed, the velocity dispersion in open clusters is small, below ∼ 1 km∕s.

Since molecular gas is concentrated close to the Galactic plane, such star clusters in the Milky Way are born there. Most of the open clusters known have ages below 300 Myr, and those are found within ∼ 50 pc of the Galactic plane. Older clusters can have larger | z | , as they can move from their place of birth, similar to what we said about the stars in the thick disk. The reason why we see only a few open clusters with ages above 1 Gyr is that these are not strongly gravitationally bound, if at all. Hence, in the course of time, tidal gravitational forces dissolve such clusters, and this effect is more important at small galactocentric radii R.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig13_HTML.jpg

Fig. 2.13

A sketch of the plane of the Milky Way, based to a large degree on observations from the Spitzer Space Telescope. It shows the two major spiral arms which originate at the ends of the central bar, as well as two minor spiral arms. The Sun is located near the Orion arm, a partial spiral arm. Credit: NASA/JPL-Caltech/R. Hurt (SSC/Caltech)

Observing the gas in the Galaxy is made possible mainly by the 21 cm line emission of Hi (neutral atomic hydrogen) and by the emission of CO, the second-most abundant molecule after H₂ (molecular hydrogen). H₂ is a symmetric molecule and thus has no electric dipole moment, which is the main reason why it does not radiate strongly. In most cases it is assumed that the ratio of CO to H₂ is a universal constant (called the ‘X-factor’ ). Under this assumption, the distribution of CO can be converted into that of the total molecular gas. The Milky Way is optically thin at 21 cm, i.e., 21 cm radiation is not absorbed along its path from the source to the observer. With radio-astronomical methods it is thus possible to observe atomic gas throughout the entire Galaxy.

Fig. 2.14

Distribution of dust in the Galaxy, derived from a combination of IRAS and COBE sky maps. The northern Galactic sky in Galactic coordinates is displayed on the left, the southern on the right. We can clearly see the concentration of dust towards the Galactic plane, as well as regions with a very low column density of dust; these regions in the sky are particularly well suited for very deep extragalactic observations. Source: D.J. Schlegel, D.P. Finkbeiner & M. Davis 1998, Maps of Dust Infrared Emission for Use in Estimation of Reddening and Cosmic Microwave Background Radiation Foregrounds, ApJ 500, 525, p. 542, Fig. 8. ©AAS. Reproduced with permission

Distribution of dust. To examine the distribution of dust, two options are available. First, dust is detected by the extinction it causes. This effect can be analyzed quantitatively, for instance by star counts or by investigating the reddening of stars (an example of this can be seen in Fig. 2.8). Second, dust emits thermal radiation, observable in the FIR part of the spectrum, which was mapped by several satellites such as IRAS and COBE. By combining the sky maps of these two satellites at different frequencies, the Galactic distribution of dust was determined. The dust temperature varies in a relatively narrow range between ∼ 17 and ∼ 21 K, but even across this small range, the dust emission varies, for fixed column density, by a factor ∼ 5 at a wavelength of 100 μm. Therefore, one needs to combine maps at different frequencies in order to determine column densities and temperatures. In addition, the zodiacal light caused by the reflection of Solar radiation by dust inside our Solar system has to be subtracted before the Galactic FIR emission can be analyzed. This is possible with multi-frequency data because of the different spectral shapes. The resulting distribution of dust is displayed in Fig. 2.14. It shows the concentration of dust around the Galactic plane, as well as large-scale anisotropies at high Galactic latitudes. The dust map shown here is routinely used for extinction correction when observing extragalactic sources.

Besides a strong concentration towards the Galactic plane, gas and dust are preferentially found in spiral arms where they serve as raw material for star formation. Molecular hydrogen (H₂) and dust are generally found at 3 kpc ≲ R ≲ 8 kpc, within $\left \vert z\right \vert \lesssim 90\,\mathrm{pc}$ of both sides of the Galactic plane. In contrast, the distribution of atomic hydrogen (Hi) is observed out to much larger distances from the Galactic center (R ≲ 25kpc), with a scale height of ∼ 160 pc inside the Solar orbit, R ≲ R ₀. At larger distances from the Galactic center, R ≳ 12 kpc, the scale height increases substantially to ∼ 1 kpc. The gaseous disk is warped at these large radii though the origin of this warp is unclear. For example, it may be caused by the gravitational field of the Magellanic Clouds. The total mass in the two components of hydrogen is about M(Hi) ≈ 4 × 10⁹ M _⊙ and $M(\mathrm{H}_{2}) \approx 10^{9}M_{\odot }$ , respectively, i.e., the gas mass in our Galaxy is less than ∼ 10 % of the stellar mass. The density of the gas in the Solar neighborhood is about $\rho (\mathrm{gas}) \sim 0.04M_{\odot }/\mathrm{pc}^{3}$ .

Phases of the interstellar medium. Gas in the Milky Way exists at a range of different temperatures and densities. The coolest phase of the interstellar medium is that represented by molecular gas. Since molecules are easily destroyed by photons from hot stars, they need to be shielded from the interstellar radiation field, which is provided by the dust embedded in the gas. The molecules can cool the gas efficiently even at low temperatures: through collisions between particles, part of the kinetic energy can be used to put one of the particles into an excited state, and thus to remove kinetic energy from the particle distribution, thereby lowering their mean velocity and, thus, their temperature. This is possible only if the kinetic energy is high enough for this internal excitation. Molecules have excited levels at low energies—the rotational and vibrational excitations—so they are able to cool cold gas; in fact, this is the necessary condition for the formation of stars. The energy in the excited level is then released by the emission of a photon which can escape. The range of temperatures in the molecular gas phase extends from ∼ 10 K to about 70 K, with characteristic densities of 100 particles per cm³.

A second prominent phase is the warm interstellar gas, with temperatures of a few thousand degrees. Depending on T, the fraction of atoms which are ionized, i.e., the ionization fraction, can range from 0.01 to 1. This gas can be heated by hydrodynamical processes or by photoionization. For example, gas near to a hot star will be ionized by the energetic photons. The kinetic energy of the electron released in this photoionization process is the difference between the energy of the ionizing photon and the binding energy of the electron. The energy of the electron is then transferred to the gas through collisions, thus providing an effective heating source. Cooling is provided by atomic transitions excited by collisions between atoms, or recombination of atoms with electrons, and the subsequent emission of photons from the excited states. Since hydrogen is by far the most abundant species, its atomic transitions dominate the cooling for T ≳ 5000 K, and is then a very efficient coolant. Because of that, the temperature of this warm gas tends towards T ∼ 8000 K, almost independent of the intensity and spectrum of the ionizing radiation, at least over a wide range of these parameters. Perhaps the best known examples for this gas are the aforementioned Hii regions around hot stars, and planetary nebulae.

2.3.4 Cosmic rays

The magnetic field of the Galaxy. Like many other cosmic objects, the Milky Way contains a magnetic field. The properties of this field can be analyzed using a variety of methods, and we list some of them in the following.

Polarization of stellar light. The light of distant stars is partially polarized, with the degree of polarization being strongly related to the extinction, or reddening, of the star. This hints at the polarization being linked to the dust causing the extinction. The light scattered by dust particles is partially linearly polarized, with the direction of polarization depending on the alignment of the dust grains. If their orientation was random, the superposition of the scattered radiation from different dust particles would add up to a vanishing net polarization. However, a net polarization is measured, so the orientation of dust particles cannot be random, rather it must be coherent on large scales. Such a coherent alignment is provided by a large-scale magnetic field, whereby the orientation of dust particles, measurable from the polarization direction, indicates the (projected) direction of the magnetic field.
The Zeeman effect. The energy levels in an atom change if the atom is placed in a magnetic field. Of particular importance in the present context is the fact that the 21 cm transition line of neutral hydrogen is split in a magnetic field. Because the amplitude of the line split is proportional to the strength of the magnetic field, the field strength can be determined from observations of this Zeeman effect.
Synchrotron radiation. When relativistic electrons move in a magnetic field they are subject to the Lorentz force. The corresponding acceleration is perpendicular both to the velocity vector of the particles and to the magnetic field vector. As a result, the electrons follow a helical (i.e., corkscrew) track, which is a superposition of circular orbits perpendicular to the field lines and a linear motion along the field. Since accelerated charges emit electromagnetic radiation, this helical movement is the source of the so-called synchrotron radiation (which will be discussed in more detail in Sect. 5.1.2). This radiation, which is observable at radio frequencies, is linearly polarized, with the direction of the polarization depending on the direction of the magnetic field.
Faraday rotation. If polarized radiation passes through a magnetized plasma, the direction of the polarization rotates. The rotation angle depends quadratically on the wavelength of the radiation,

$\displaystyle{ \varDelta \theta = \mathrm{RM}\,\lambda ^{2}\;. }$

(2.38)

The rotation measure RM is the integral along the line-of-sight towards the source over the electron density and the component B _∥ of the magnetic field in direction of the line-of-sight,

$\displaystyle{ \mathrm{RM} = 81\,\mathrm{ \frac{rad} {cm^{2}}}\int _{0}^{D} \frac{\mathrm{d}\ell} {\mathrm{pc}}\; \frac{n_{\mathrm{e}}} {\mathrm{cm}^{-3}}\,\frac{B_{\parallel }} {\mathrm{G}} \;. }$

(2.39)

The dependence of the rotation angle (2.38) on λ allows us to determine the rotation measure RM, and thus to estimate the product of electron density and magnetic field. If the former is known, one immediately gets information about B. By measuring the RM for sources in different directions and at different distances the magnetic field of the Galaxy can be mapped.

From applying the methods discussed above, we know that a magnetic field exists in the disk of our Milky Way. This field has a strength of about 4 × 10⁻⁶ G and mainly follows the spiral arms.

Cosmic rays. We obtain most of the information about our Universe from the electromagnetic radiation that we observe. However, we receive an additional radiation component, the energetic cosmic rays, which were discovered by Victor Hess in 1912 who carried out balloon flights and found that the degree of ionizing radiation increases with increasing height. Cosmic rays consist primarily of electrically charged particles, mainly electrons and nuclei. In addition to the particle radiation that is produced in energetic processes at the Solar surface, a much more energetic cosmic ray component exists that can only originate in sources outside the Solar system.

Fig. 2.15

The energy spectrum dN∕dE of cosmic rays, for better visibility multiplied by E ². Data from different experiments are shown by different symbols. At energies below 10¹⁰ eV (not shown), the flux of cosmic rays is dominated by those from the Sun, whereas for higher energies, they are due to sources in our Galaxy or beyond. The energy spectrum is well described by piecewise power-law spectra, with a steepening at E ∼ 10¹⁵ eV (called the knee), and a flattening at E ∼ 3 × 10¹⁸ eV. Beyond E ∼ 3 × 10¹⁹ eV, the spectrum shows a cut-off. Also indicated is the energy of a cosmic ray proton whose collision with a proton in the Earth’ atmosphere has the same center-of-mass energy as the highest energy collisions at the Large Hadron Collider at CERN. The cosmic ray fluxes are very small: cosmic rays with energies larger than ∼ 10¹⁵ eV arrive at the Earth at a rate of about 1 per m² per year, those with energies above 10¹⁸ eV come at a rate of approximately $1\,\mathrm{km^{-2}yr^{-1}}$ ; this implies that one needs huge detectors to study these particles. Source: K. Kotera & A.V. Olinto 2011, The Astrophysics of Ultrahigh-Energy Cosmic Rays, ARA&A 49, 119, p. 120, Fig. 1. Reprinted, with permission, from the Annual Review of Astronomy & Astrophysics, Volume 49 ©2011 by Annual Reviews www.annualreviews.org

The energy spectrum of the cosmic rays is, to a good approximation, a power law: the flux of particles with energy between E and E + dE can be written as $(\mathrm{d}N/\mathrm{d}E)\,\mathrm{d}E \propto E^{-q}\,\mathrm{d}E$ , with q ≈ 2. 7. However, as can be seen in Fig. 2.15, the slope of the spectrum changes slightly, but significantly, at some energy scales: at E ∼ 10¹⁵ eV the spectrum becomes steeper, and at E ≳ 10¹⁸ eV it flattens again¹⁰; these two energy scales in the cosmic ray spectrum have been given the suggestive names of ‘knee’ and ‘ankle’, respectively. Measurements of the spectrum at these high energies are rather uncertain, however, because of the strongly decreasing flux with increasing energy. This implies that only very few particles are detected.

Cosmic ray acceleration and confinement. To accelerate particles to such high energies , very energetic processes are necessary. For energies below 10¹⁵ eV, very convincing arguments suggest supernova remnants as the sites of the acceleration. The SN explosion drives a shock front¹¹ into the ISM with an initial velocity of ∼ 10 000 km∕s. Plasma processes in a shock front can accelerate some particles to very high energies. The theory of this diffuse shock acceleration predicts that the resulting energy spectrum of the particles follows a power law, the slope of which depends only on the strength of the shock (i.e., the ratio of the densities on both sides of the shock front). This power law agrees very well with the slope of the observed cosmic ray spectrum below the knee, if additional effects caused by the propagation of particles in the Milky Way (e.g., energy losses, and the possibility for escaping the Galaxy) are taken into account. The presence of very energetic electrons in SN remnants is observed directly by their synchrotron emission, so that the slope of the produced spectrum can be inferred by observations.

Accelerated particles then propagate through the Galaxy where, due to the magnetic field, they move along complicated helical tracks. Therefore, the direction from which a particle arrives at Earth cannot be identified with the direction to its source of origin. The magnetic field is also the reason why particles do not leave the Milky Way along a straight path, but instead are stored for a long time ( ∼ 10⁷ yr) before they eventually diffuse out, an effect called confinement.

The sources of the particles with energy between ∼ 10¹⁵ eV and ∼ 10¹⁸ eV are likewise presumed to be located inside our Milky Way, because the magnetic field is sufficiently strong to confine them in the Galaxy. It is not known, however, whether these particles are also accelerated in supernova remnants; if they are, the steepening of the spectrum may be related to the fact that particles with E ≳ 10¹⁵ eV have a Larmor radius which no longer is small compared to the size of the remnant itself, and so they find it easier to escape from the accelerating region. Particles with energies larger than ∼ 10¹⁸ eV are probably of extragalactic origin. The radius of their helical tracks in the magnetic field of the Galaxy, i.e., their Larmor radius, is larger than the radius of the Milky Way itself, so they cannot be confined. Their origin is also unknown, but AGNs are the most probable source of these particles.

Ultra-high energy cosmic rays. Finally, one of the largest puzzles of high-energy astrophysics is the origin of cosmic rays with E ≳ 10¹⁹ eV. The energy of these so-called ultra-high energy cosmic rays (UHECRs) is so large that they are able to interact with the cosmic microwave background to produce pions and other particles, losing much of their energy in this process. These particles cannot propagate much further than ∼ 100 Mpc through the Universe before they have lost most of their energy. This implies that their acceleration sites should be located in the close vicinity of the Milky Way. Since the curvature of the orbits of such highly energetic particles is very small, it should, in principle, be possible to identify their origin: there are not many AGNs within 100 Mpc that are promising candidates for the origin of these ultra-high energy cosmic rays. Furthermore, the maximal possible distance a cosmic ray particle can propagate through the Universe decreases strongly with increasing energy, so that the number of potential sources must decrease accordingly. Once this minimal distance is below the nearest AGN, there should be essentially no particle that can reach us. In other words, one expects to see a cut-off (called the Greisen–Zatsepin–Kuzmin, or GZK cut-off) in the energy spectrum at E ∼ 2 × 10²⁰ eV, but beginning already at E ≳ 5 × 10¹⁹ eV. Before 2007, this cut-off was not observed, and different cosmic ray experiments reported a different energy spectrum for these UHECRs—based, literally, on a handful of events.

The breakthrough came with the first results from the Auger experiment, the by far most sensitive experiment owing to its large effective area.¹² When the first results were published in 2007, the expected high-energy cut-off in the UHECR spectrum was detected—thereby erasing the necessity for many very exotic processes that had been proposed earlier to account for the apparent lack of this cut-off. With this detection the idea about the origin of the UHECRs from sources within a distance of ∼ 100 Mpc is strongly supported. But if this is indeed the case, these sources should be identified.

Indeed, a correlation between the arrival direction of UHECRs and the direction of nearby AGN has been found, providing evidence that these are the places in which particles can be accelerated to such high energies. From a statistical analysis of this correlation, the typical angular separation between the cosmic ray and the corresponding AGN is estimated to be ∼ 3^∘, which may be identified with the deflection of direction that a cosmic ray experiences on its way to Earth, most likely due to magnetic fields. Whereas substantially increased statistics, possible with accumulating data, is needed to confirm this correlation, the big puzzle about the UHECRs may have found a solution.

Energy density. It is interesting to realize that the energy densities of cosmic rays, the magnetic field, the turbulent energy of the ISM, and the electromagnetic radiation of the stars are about the same—as if an equilibrium between these different components has been established. Since these components interact with each other—e.g., the turbulent motions of the ISM can amplify the magnetic field, and vice versa, the magnetic field affects the velocity of the ISM and of cosmic rays—it is not improbable that these interaction processes can establish an equipartition of the energy densities.

Gamma radiation from the Milky Way. The Milky Way emits γ-radiation, as can be seen in Fig. 1.8. There is diffuse γ-ray emission which can be traced back to the cosmic rays in the Galaxy. When these energetic particles collide with nuclei in the interstellar medium, radiation is released. This gives rise to a continuum radiation which closely follows a power-law spectrum, such that the observed flux S _ν is ∝ ν ^−α , with α ∼ 2. The quantitative analysis of the distribution of this emission provides the most important information about the spatial distribution of cosmic rays in the Milky Way.

Gamma-ray lines. In addition to the continuum radiation, one also observes line radiation in γ-rays, at energies below ∼ 10 MeV. The first detected and most prominent line has an energy of 1. 809 MeV and corresponds to a radioactive decay of the Al²⁶ nucleus. The spatial distribution of this emission is strongly concentrated towards the Galactic disk and thus follows the young stellar population in the Milky Way. Since the lifetime of the Al²⁶ nucleus is short ( ∼ 10⁶ yr), it must be produced near the emission site, which then implies that it is produced by the young stellar population. It is formed in hot stars and released to the interstellar medium either through stellar winds or core-collapse supernovae. Gamma-lines from other radioactive nuclei have been detected as well.

Annihilation radiation from the Galaxy. Furthermore, line radiation with an energy of 511 keV has been detected in the Galaxy. This line is produced when an electron and a positron annihilate into two photons, each with an energy corresponding to the rest-mass energy of an electron, i.e., 511 keV.¹³ This annihilation radiation was identified first in the 1970s. With the Integral satellite, its emission morphology has been mapped with an angular resolution of ∼ 3^∘. The 511 keV line emission is detected both from the Galactic disk and the bulge. The angular resolution is not sufficient to tell whether the annihilation line traces the young stellar population (i.e., the thin disk) or the older population in the thick disk. However, one can compare the distribution of the annihilation radiation with that of Al²⁶ and other radioactive species. In about 85 % of all decays Al²⁶ emits a positron. If this positron annihilates close to its production site one can predict the expected annihilation radiation from the distribution of the 1. 809 MeV line. In fact, the intensity and angular distribution of the 511 keV line from the disk are compatible with this scenario for the generation of positrons.

The origin of the annihilation radiation from the bulge, which has a luminosity larger than that from the disk by a factor ∼ 5, is unknown. One needs to find a plausible source for the production of positrons in the bulge. There is no unique answer to this problem at present, but Type Ia supernovae and energetic processes near low-mass X-ray binaries are prime candidates for this source.

2.3.5 The Galactic bulge

The Galactic bulge is the central thickening of our Galaxy. Figure 1.2 shows another spiral galaxy from its side, with its bulge clearly visible. Compared to that, the bulge in the Milky Way is far more difficult to identify in the optical, as can be seen in Fig. 2.1, owing to obscuration. However, in the near-IR, it clearly sticks out (Fig. 1.8). The characteristic scale-length of the bulge is ∼ 1 kpc. Owing to the strong extinction in the disk, the bulge is best observed in the IR. The extinction to the Galactic center in the visual is A _V ∼ 28 mag. However, some lines-of-sight close to the Galactic center exist where A _V is significantly smaller, so that observations in optical and near-IR light are possible, e.g., in Baade’s Window, located about 4^∘ below the Galactic center at ℓ ∼ 1^∘, for which A _V ∼ 2mag (also see Sect. 2.6).

From the observations by COBE, and also from Galactic microlensing experiments (see Sect. 2.5), we know that our bulge has the shape of a peanut-shaped bar , with the major axis pointing away from us by about 25^∘. The scale-height of the bulge is ∼ 400 pc, with an axis-ratio of ∼ 1: 0. 35: 0. 26.

As is the case for the exponential profiles that describe the light distribution in the disk, the functional form of the brightness distribution in the bulge is also suggested from observations of other spiral galaxies. The profiles of their bulges, observed from the outside, are much better determined than in our Galaxy where we are located amid its stars.

The de Vaucouleurs profile. The brightness profile of our bulge can be approximated by the de Vaucouleurs law which describes the surface brightness I as a function of the projected distance R from the center,

$\displaystyle{ \fbox{$\log \left (\frac{I(R)} {I_{\mathrm{e}}} \right ) = -3.3307\left [\left ( \frac{R} {R_{\mathrm{e}}}\right )^{1/4} - 1\right ]$}\;, }$

(2.40)

with I(R) being the measured surface brightness, e.g., in $[I] = L_{\odot }/\mathrm{pc}^{2}$ . R _e is the effective radius, defined such that half of the luminosity is emitted from within R _e,

$\displaystyle{ \int _{0}^{R_{\mathrm{e}} }\mathrm{d}R\;R\,I(R) = \frac{1} {2}\int _{0}^{\infty }\mathrm{d}R\;R\,I(R)\;. }$

(2.41)

This definition of R _e also leads to the numerical factor on the right-hand side of (2.40). As one can easily see from (2.40), I _e = I(R _e) is the surface brightness at the effective radius. An alternative form of the de Vaucouleurs law is

$\displaystyle{ \fbox{$I(R) = I_{\mathrm{e}}\,\exp \left (-7.669\left [(R/R_{\mathrm{e}})^{1/4} - 1\right ]\right )$}\;. }$

(2.42)

Because of its mathematical form, it is also called an r ^1∕4 law. The r ^1∕4 law falls off significantly more slowly than an exponential law for large R. For the Galactic bulge, one finds an effective radius of R _e ≈ 0. 7 kpc. With the de Vaucouleurs profile, a relation between luminosity, effective radius, and surface brightness is obtained by integrating over the surface brightness,

$\displaystyle{ \fbox{$L =\int _{ 0}^{\infty }\mathrm{d}R\;2\pi R\,I(R) = 7.215\pi I_{\mathrm{ e}}\,R_{\mathrm{e}}^{2}$}\;. }$

(2.43)

Fig. 2.16

The ratio of magnesium and iron, as a function of metallicity [Fe/H]. Filled grey circles correspond to bulge stars, red (blue) circles show nearby stars from the thick (thin) disk. The dotted lines corresponds to the Solar value. Source: T. Bensby et al. 2013, Chemical evolution of the Galactic bulge as traced by microlensed dwarf and subgiant stars. V. Evidence for a wide age distribution and a complex MDF, A&A 549, A147, Fig. 27. ©ESO. Reproduced with permission

Stellar age distribution in the bulge.

The stars in the bulge cover a large range in metallicity, $-1 \lesssim [\mathrm{Fe}/\mathrm{H}] \lesssim +0.6$ , with a mean of about 0.3, i.e., the mean metallicity is about twice that of the Sun. The metallicity also changes as a function of distance from the center, with more distant stars having a smaller value of [Fe/H].

The high metallicity means that either the stars of the bulge formed rather late, according to the age-metallicity relation, or that it is an old population with very intense star formation activities at an early cosmic epoch. We can distinguish between these two possibilities from the chemical composition of stars in the bulge, obtained from spectroscopy. This is shown in Fig. 2.16, where the magnesium-to-iron ratio is shown for stars in the bulge and compared to disk stars. Obviously, bulge stars have a significantly higher abundance of Mg, relative to iron, than the stars from the thin disk, but much more similar to thick disk stars. Recalling the discussion of the chemical enrichment of the interstellar medium by supernovae in Sect. 2.3.2, this implies that the enrichment must have occurred predominantly by core-collapse supernovae, since they produce a high ratio of α-elements (like magnesium) compared to iron, whereas Type Ia SNe produce mainly iron-group elements. Therefore, most of the bulge stars must have formed before the Type Ia SNe exploded. Whereas the time lag between the birth of a stellar population and the explosion of the bulk of Type Ia SN is not well known (it depends on the evolution of binary systems), it is estimated to be between 1 and 3 Gyr. Hence, most of the bulge stars must have formed on a rather short time-scale: the bulge consists mainly of an old stellar population, formed within ∼ 1 Gyr. This is also confirmed with the color-magnitude diagram of bulge stars from which an age of 10 ± 2. 5 Gyr is determined.

However, in the region of the bulge, one also finds stars that kinematically belong to the disk and the halo, as both extend to the inner region of the Milky Way. The thousands of RR Lyrae stars found in the bulge, for example, have a much lower metallicity than typical bulge stars and may well belong to the innermost region of the stellar halo, and younger stars may be part of the disk population.

The mass of the bulge is about $M_{\mathrm{bulge}} \sim 1.6 \times 10^{10}M_{\odot }$ and its luminosity is $L_{B,\mathrm{bulge}} \sim 3 \times 10^{9}L_{\odot }$ , which results in a stellar mass-to-light ratio of

$\displaystyle{ \fbox{$\frac{M} {L} \approx 5\frac{M_{\odot }} {L_{\odot }} \;\;\mbox{ in the bulge}$}\;, }$

(2.44)

larger than that of the thin disk.

2.3.6 The stellar halo

The visible halo of our Galaxy consists of about 150 globular clusters and field stars with a high velocity component perpendicular to the Galactic plane. A globular cluster is a collection of typically several hundred thousand stars, contained within a spherical region of radius ∼ 20 pc. The stars in the cluster are gravitationally bound and orbit in the common gravitational field. The old globular clusters with $[\mathrm{Fe/H}] <-0.8$ have an approximately spherical distribution around the Galactic center. A second population of globular clusters exists that contains younger stars with a higher metallicity, $[\mathrm{Fe/H}]> -0.8$ . They have a more oblate geometrical distribution and are possibly part of the thick disk because they show roughly the same scale-height. The total mass of the stellar halo in the radius range between 1 and 40 kpc is $\sim 4 \times 10^{8}M_{\odot }$ .

Most globular clusters are at a distance of r ≲ 35 kpc (with $r = \sqrt{R^{2 } + z^{2}}$ ) from the Galactic center, but some are also found at r > 60 kpc. At these distances it is hard to judge whether these objects are part of the Galaxy or whether they have been captured from a neighboring galaxy, such as the Magellanic Clouds. Also, field stars have been found at distances out to r ∼ 50 kpc, which is the reason why one assumes a characteristic value of r _halo ∼ 50 kpc for the extent of the visible halo.

The density distribution of metal-poor globular clusters and field stars in the halo is described by

$\displaystyle{ n(r) \propto r^{-\gamma }\;, }$

(2.45)

with a slope γ in the range 3–3.5. Alternatively, one can fit a de Vaucouleurs profile to the density distribution, which results in an effective radius of r _e ∼ 2. 7 kpc. Star counts from the Sloan Digital Sky Survey provided clear indications that the stellar halo of the Milky Way is flattened, i.e., it is oblate, with an axis ratio of the smallest axis (in the direction of the rotation axis) to the longer ones being q ∼ 0. 6.

Furthermore, the SDSS discovered the fact that the stellar halo is highly structured: the distribution of stars in the halo is not smooth, but local over- and underdensities are abundant. Several so-called stellar streams were found, regions of stellar overdensities with the shape of a long and narrow cylinder. These stellar streams can in some cases be traced back to the disruption of a low-mass satellite galaxy of the Milky Way by tidal gravitational forces, most noticeably to the Sagittarius dwarf spheroidal (Sgr dSph).

Tidal disruption. Consider a system of gravitationally bound particles, such as a star cluster, a star, or a gas cloud, moving in a gravitational field. The trajectory of the system is determined by the gravitational acceleration. However, since the system is extended, particles in the outer part of the system experience a different gravitational acceleration than the center of mass. Hence, in the rest frame of the moving system, there is a net acceleration of the particles away from the center, due to tidal gravitational forces. The best-known example of this are the tides on Earth: whereas the Earth is freely falling in the gravitational field caused by the Sun (and the Moon), matter on its surface experiences a net force, since the gravitational field is inhomogeneous, giving rise to the tides. If this net force for particles in the outer part of the system is directed outwards, and stronger than the gravitational force binding the particles to the system, these particles will be removed from the system—the system will lose particles due to this tidal stripping.

Fig. 2.17

Tidal disruption of the globular cluster Palomar 5. Left panel: The white blob shows the globular cluster, from which the two tidal tails emerge, shown in orange. These contain more mass than the cluster itself at the current epoch, meaning the cluster has lost more than half its original mass. The tidal tails delineate the cluster’s orbit around the Galaxy, which is sketched in the right panel as the red curve, with the current position of Pal 5 indicated in green. Credit: M. Odenkirchen, E. Grebel, Max-Planck-Institut für Astronomie, and the Sloan Digital Sky Survey Collaboration

Condition for tidal disruption. We can consider this process more quantitatively. Consider a spherical system of mass M and radius R, so the gravitational acceleration on the surface is $a_{\mathrm{s}} = -GM/R^{2}$ , directed inwards. If $\phi ({\boldsymbol r})$ is the gravitational potential in which this system moves, the tidal acceleration ${\boldsymbol a}_{\mathrm{tid}}$ is the difference between the acceleration −∇ϕ at the surface of the system and that at its center,

$\displaystyle{{\boldsymbol a}_{\mathrm{tid}}({\boldsymbol R}) ={\boldsymbol a}({\boldsymbol r} +{\boldsymbol R}) -{\boldsymbol a}({\boldsymbol r})\;,}$

where ${\boldsymbol R}$ is a vector from the center of the system to its surface, i.e., $\vert {\boldsymbol R}\vert = R$ . A first-order Taylor expansion of the term on the r.h.s. yields for the i-component of the tidal acceleration

$\displaystyle{a_{\mathrm{tid},i} = -\sum _{j=1}^{3} \frac{\partial ^{2}\phi } {\partial r_{i}\partial r_{j}}R_{j} \equiv -\sum _{j=1}^{3}\phi _{,ij}R_{j}\;,}$

where we made use of the fact that ${\boldsymbol a} = -\nabla \phi$ , and the derivatives are taken at the center of the system. In the final step, we abbreviated the matrix of second partial derivatives of ϕ with ϕ _, ij . This matrix is symmetric, and therefore one can always rotate to a coordinate system in which this matrix is diagonal. We will assume now that the local matter density ρ causing the potential ϕ vanishes; then, from the Poisson equation ∇² ϕ = 4π G ρ, we find that the sum of the diagonal elements of ϕ _, ij is zero. Furthermore, we assume that the tidal field is axially symmetric, with the r ₁-axis being the axis of symmetry. In this case, we can write the tidal matrix as $\phi _{,ij} = \mathrm{diag}(-2t,t,t)$ . Writing the radius vector as ${\boldsymbol R} = R(\cos \theta,\sin \theta, 0)$ , i.e., restricting it to the r ₁-r ₂-plane, the tidal acceleration becomes ${\boldsymbol a}_{\mathrm{tid}} = tR(2\cos \theta,-\sin \theta, 0)$ . The radial component of the tidal acceleration is obtained by projecting ${\boldsymbol a}_{\mathrm{tid}}$ along the radial direction,

$\displaystyle{a_{\mathrm{tid,r}} ={\boldsymbol a}_{\mathrm{tid}} \frac{{\boldsymbol R}} {\vert {\boldsymbol R}\vert }=tR\left (2\cos ^{2}\theta -\sin ^{2}\theta \right )=tR\left (3\cos ^{2}\theta - 1\right )\;.}$

The total radial acceleration is then

$\displaystyle{a_{\mathrm{tot,r}} = -\frac{GM} {R^{2}} + a_{\mathrm{tid,r}}\;.}$

If this is positive, the net force on a particle is directed outwards, and the particle is stripped from the system. Obviously, a _tid,r depends on the position on the surface, here described by θ. Note that the radial component of the tidal acceleration is symmetric under θ → θ +π, i.e., is the same at opposite points on the sphere. This is in agreement with the observation that the tide gauge has two maxima and two minima at any time on the Earth surface, so that the period of the tidal motion is 12 h, i.e., half a day. Also note that in some regions on the surface, the tidal acceleration is directed inwards, and directed outwards at other points. If there is one point where the total radial acceleration is positive, i.e., directed outwards, the system will lose mass. Assuming t > 0, this happens if 2tR > GM∕R ². In other words, for a system to be stable against tidal stripping, one must have

$\displaystyle{ t <\frac{GM} {2R^{3}} = \frac{2\pi G} {3} \bar{\rho }\;, }$

(2.46)

where in the final expression we inserted the mean density $\bar{\rho }$ of the system. Hence, for a given mean density of a system, the tidal gravitational field must not be larger than (2.46) in order for the system to remain stable against tidal stripping.

One application of the foregoing treatment is the disruption of a system in the field of a point mass M _p, given by $\phi ({\boldsymbol r}) = -GM_{\mathrm{p}}/\vert {\boldsymbol r}\vert$ . If we choose the system to be located on the r ₁-axis, the tidal matrix ϕ _, ij is diagonal and reads

$\displaystyle{\phi _{,ij} = (GM_{\mathrm{p}}/r^{3})\,\mathrm{diag}(2,-1,-1)\;.}$

Thus, the system is disrupted if

$\displaystyle{ \frac{2GM_{\mathrm{p}}} {r^{3}}> \frac{GM} {R^{3}} \;. }$

(2.47)

We will return to this example when we consider the tidal disruption of stars in the gravitational field of a black hole.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig18_HTML.jpg

Fig. 2.18

The “Field of Streams”, as detected in the SDSS survey. Shown is the two-dimensional distribution of stars, which were color selected by g − r < 0. 4, and magnitude selected by 19 ≤ r ≤ 22. The color selection yields the bluest stars in an old stellar population corresponding to those whose main-sequence lifetime equals the age of the population; hence, they are main sequence turn-off stars. The range in magnitude then corresponds to a corresponding range in distance. The distances are color-coded in this figure, with blue corresponding to the nearest stars at D ∼ 10 kpc, and red to the most distant ones at D ∼ 30 kpc. One sees that the density of stars is far from uniform, but that several almost one-dimensional overdensities are easily identified. The most prominent of these streams, the Sagittarius stream, corresponds to stars which have been tidally stripped from the Sgr dSph. There is a clear distance gradient along the stream visible, with the most distant stars in the lower left of the image. Note that this image covers almost a quarter of the sky. Credit: Vasily Belokurov, SDSS-II Collaboration

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig19_HTML.jpg

Fig. 2.19

Hi-map of a large region in the sky containing the Magellanic Clouds. This map is part of a large survey of Hi, observed through its 21 cm line emission, that was performed with the Parkes telescope in Australia, and which maps about a quarter of the Southern sky with a pixel size of 5′ and a velocity resolution of ∼ 1 km∕s. The emission from gas at Galactic velocities was removed in this map. Besides the Hi emission by the Magellanic Clouds themselves, gas between them is visible, the Magellanic Bridge and the Magellanic Stream, the latter connected to the Magellanic Clouds by an ‘Interface Region’. Gas is also found in the direction of the orbital motion of the Magellanic Clouds around the Milky Way, forming the ‘Leading Arm’. Source: C. Brüns et al. 2005, The Parkes H i Survey of the Magellanic System, A&A 432, 45, p. 50, Fig. 2. ©ESO. Reproduced with permission

On its orbit through the Milky Way, a satellite galaxy or a star cluster will experience a tidal force which varies with time. When it gets closer to the center, or to the disk, one expects the tidal field to get stronger than on other parts of the orbit. Depending on its mean density and its orbit, such a system will lose mass in the course of time. This is impressively seen in the globular cluster Pal 5, where the SDSS has found two massive tidal tails of stars that were removed from the cluster due to tidal forces (Fig. 2.17). The 180^∘-symmetry of the tidal force mentioned before leads to the occurrence of two almost symmetric tidal tails, one moving slightly faster than the cluster (the leading tail), the other slower (trailing tail). The tidally stripped stars form such coherent structures since their velocity dispersion is very small, comparable to the velocity dispersion of the globular cluster. This explains why such tidal streams form a distinct feature for a long time. Since the tidal tails of Pal 5 contain more stellar mass than the remaining cluster, the latter has lived through the best part of its life and will be totally disrupted within its next few orbits around the Galactic center.

As mentioned above, other stellar streams similar to that of Pal 5 have been found, the clearest one being that related to the tidal disruption of Sgr dSph. The corresponding tidal stream is observed to create a full great circle on the sky; a part of it is shown in Fig. 2.18.

As we will discuss later (see Chap. 10), the strong substructure of the stellar halo is expected from our understanding of the evolution of galaxies where galaxies grow in mass through mergers with other galaxies. In this model, the observed substructure are remnants of low-mass galaxies which were accreted onto the Milky Way at some earlier time—in agreement with the discussion above on the possible origin of the thick disk.

2.3.7 The gaseous halo

Besides a stellar component, also gas in various phases is seen outside the disk of the Milky Way. The gas is detected either by its emission or by absorption lines in the spectra of sources located at larger distances. When observing gas, either in emission or absorption, its distance to us is at first unknown, and must be inferred indirectly.

Infalling gas clouds. Neutral hydrogen is observed outside the Galactic disk, in the form of clouds. Most of these clouds, visible in 21 cm line emission, have a negative radial velocity, i.e., they are moving towards us, with velocities of up to $v_{\mathrm{r}} \sim -400\,\mathrm{km/s}$ . Based on their observed velocity, these high-velocity clouds (HVCs) cannot be following the general Galactic rotation. In addition, there are clouds with smaller velocities, the intermediate-velocity clouds (IVCs).

These clouds are often organized in big structures on the sky, the largest of which are located close to the Magellanic Clouds (Fig. 2.19). This gas forms the Magellanic Stream, a narrow band of Hi emission which follows the Magellanic Clouds along their orbit around the Galaxy (see Fig. 2.20). This gas stream may be the result of a close encounter of the Magellanic Clouds with the Milky Way in the past. The (tidal) gravitational force that the Milky Way had imposed on our neighboring galaxies in such an encounter could strip away part of their interstellar gas. For the Magellanic Stream, the distance can be assumed to coincide with the distance to the Magellanic Clouds.

For the other HVCs, which are not associated with a stellar structure, distances can be estimated through absorption. If we consider a set of stars near to the line-of-sight to a hydrogen cloud, located at different distances from us, then those at distances larger than the gas will show absorption lines caused by the gas (with the same radial velocity, or Doppler shift, as the emission of the gas), and those which are closer will not. Hence, from the interstellar absorption lines of stars in the Galactic halo, the distances to the HVCs can be inferred. These studies became possible after the Sloan Digital Sky Survey, and other imaging surveys, identified a large number of halo stars, so that we now have a pretty good three-dimensional picture of this gas distribution.

Most of the HVCs are at distances between 2 and 15 kpc from us, and within ∼ 10 kpc of the Galactic disk. Based on the line width, indicating the thermal velocity of the gas, its temperature is characteristic of a warm neutral medium, T ∼ 10⁴ K, but narrower line components in some HVCs show that cooled gas must be present as well. This neutral hydrogen has a large covering fraction, i.e., more than a third of our sky is covered down to a column density of 2 × 10¹⁷ cm⁻² in neutral hydrogen atoms.

The neutral gas in the HVCs is often associated with optical emission in the Hα line. This emission line is produced in the process of hydrogen recombination, from which one concludes that the hydrogen clouds are partially ionized, most likely due to ionizing radiation from hot stars in the Galactic disk. The total mass contained in the HVCs can be estimated to amount to ∼ 7 × 10⁷ M _⊙, if it is assumed that their neutral fraction overall is about 50 %. The hydrogen gas associated with the Magellanic Stream contains a mass at least four times this value.

Warm and hot gas. Beside the relatively cold neutral gas seen in the HVCs, there is hotter gas at large distances from the Galactic plane. Gas with temperatures of T ∼ 10⁵ K is observed through absorption lines of highly ionized species in optical and UV spectra of distance sources, like quasars. Indeed, a covering fraction larger than ∼ 60 % is found for absorption by doubly ionized silicon (Siii) and by five times ionized oxygen (Ovi). The temperature of the gas can be estimated if several different ions are detected in absorption; this then also allows one to determine the total column density of gas. It is estimated that this gas component has a metallicity of ∼ 0. 2 Solar, and a total mass of ∼ 10⁸ M _⊙.

Hotter gas, with T ∼ 10⁶ K, is seen from its X-ray emission, as well as through absorption lines of Ovii and Oviii. Most of this gas that we see in emission is believed to be within a few kiloparsecs of the Galactic disk, but there is evidence that some gas extends to larger distances. The presence of this hot gas component is also evidenced by the morphology of some HVCs, which show a head-tail structure (not unlike that of comets), best explained if the hydrogen cloud moves through an ambient medium which compresses its head, and gradually strips off gas from the cloud, which forms the tail.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig20_HTML.jpg

Fig. 2.20

The image on top displays the neutral hydrogen distribution belonging to the Magellanic Stream, shown in pink, projected onto an optical image of the sky. The Magellanic Clouds are the two white regions at the right of the region marked with the blue box. The filamentary gas ‘above’ the Magellanic Clouds is called the ‘leading arm’, whereas most of the gas between the LMC and SMC is often called the Magellanic Bridge, and the gas connecting this with the Magellanic Stream is called interface region. The bottom image is a 21 cm radio map of the that marked region, obtained as part of the Leiden-Argentine-Bonn (LAB) Survey. The crosses mark active galactic nuclei for which UV-spectra were obtained with the Cosmic Origins Spectrograph (COS) onboard HST, to measure the absorption caused by the gas. In particular, the metallicity and chemical composition of the gas was determined. Comparison with the chemical composition of the LMC and SMC shows that the gas of the Magellanic Stream most likely originated from the SMC, from which it was removed by ram-pressure and tidal stripping, though part of the Magellanic Stream was also contributed by the LMC. Credit: David L. Nidever et al., NRAO/AUI/NSF and A. Mellinger, Leiden-Argentine-Bonn (LAB) Survey, Parkes Observatory, Westerbork Observatory, and Arecibo Observatory

The gas visible outside the disk constitutes about 10 % of the total interstellar medium in the Milky Way and thus presents a significant reservoir of gas. Some of this gas is believed to have been expelled from the Galactic disk, through outflows generated by supernova explosions, based on theoretical expectations and on the measured high metallicity. This gas cools by adiabatic expansion, and returns to the disk under the influence of gravity; this is thought to be a possible origin of IVCs. Since the flow of this gas resembles that of water in a fountain, this scenario is often called the galactic fountain model. Low-metallicity gas, mainly the HVCs, may be coming from outside the Galaxy and be falling into its gravitational potential for the first time. This would then be a fresh supply of gas, out of which stars will be able to form in the future. Indeed, we believe that the mass of the Milky Way is growing also through this accretion of gas, and this is one of the elements of the models of galaxy evolution that we will discuss in Chap. 10. The inflow of gas is estimated to be a few M _⊙ per year, comparable to the star-formation rate in the Milky Way.

2.3.8 The distance to the Galactic center

As already mentioned, our distance from the Galactic center is rather difficult to measure and thus not very precisely known. The general problem with such a measurement is the high extinction in the disk, prohibiting measurements of the distance of individual stars close to the Galactic center. Thus, one has to rely on more indirect methods, and the most important ones will be outlined here.

The visible halo of our Milky Way is populated by globular clusters and also by field stars. They have a spherical, or, more generally, a spheroidal distribution. The center of this distribution is obviously identified with the center of gravity of the Milky Way, around which the halo objects are moving. If one measures the three-dimensional distribution of the halo population, the geometrical center of this distribution should correspond to the Galactic center.

Fig. 2.21

The number of RR Lyrae stars as a function of distance, measured in a direction that closely passes the Galactic center, at ℓ = 0^∘ and $b = -8^{\circ }$ . If we assume a spherically symmetric distribution of the RR Lyrae stars, concentrated towards the center, the distance to the Galactic center can be identified with the maximum of this distribution. Source: M. Reid 1993, The distance to the center of the Galaxy, ARA&A 31, 345, p. 355. Reprinted, with permission, from the Annual Review of Astronomy & Astrophysics, Volume 31 ©1993 by Annual Reviews www.annualreviews.org

This method can indeed be applied because, due to their extended distribution, halo objects can be observed at relatively large Galactic latitudes where they are not too strongly affected by extinction. As was discussed in Sect. 2.2, the distance determination of globular clusters is possible using photometric methods. On the other hand, one also finds RR Lyrae stars in globular clusters to which the period-luminosity relation can be applied. Therefore, the spatial distribution of the globular clusters can be determined. However, at about 150, the number of known globular clusters is relatively small, resulting in a fairly large statistical error for the determination of the common center. Much more numerous are the RR Lyrae field stars in the halo, for which distances can be measured using the period-luminosity relation. The statistical error in determining the center of their distribution is therefore much smaller. On the other hand, this distance to the Galactic center is based only on the calibration of the period-luminosity relation, and any uncertainty in this will propagate into a systematic error on R ₀. Effects of the extinction add to this. However, such effects can be minimized by observing the RR Lyrae stars in the NIR, which in addition benefits from the narrower luminosity distribution of RR Lyrae stars in this wavelength regime. These analyses yield a value of R ₀ ≈ 8. 0 kpc (see Fig. 2.21).

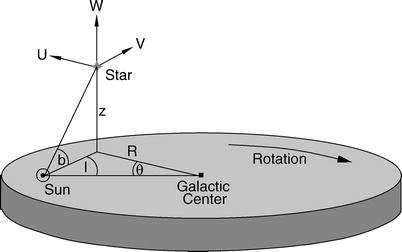
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig22_HTML.jpg

Fig. 2.22

Cylindrical coordinate system (R, θ, z) with the Galactic center at its origin. Note that θ increases in the clockwise direction if the disk is viewed from above. The corresponding velocity components (U, V, W) of a star are indicated. Adopted from B.W. Carroll & D.A. Ostlie 1996, Introduction to Modern Astrophysics, Addison-Wesley

2.4 Kinematics of the Galaxy

Unlike a solid body, the Galaxy rotates differentially. This means that the angular velocity is a function of the distance R from the Galactic center. Seen from above, i.e., from the NGP, the rotation is clockwise. To describe the velocity field quantitatively we will in the following introduce velocity components in the coordinate system (R, θ, z), as shown in Fig. 2.22. An object following a track [R(t), θ(t), z(t)] then has the velocity components

$\displaystyle{ U:= \frac{\mathrm{d}R} {\mathrm{d}t} \;,\quad V:= R \frac{\mathrm{d}\theta } {\mathrm{d}t}\;,\quad W:= \frac{\mathrm{d}z} {\mathrm{d}t}\;. }$

(2.48)

For example, the Sun is not moving on a simple circular orbit around the Galactic center, but currently inwards, U < 0, and with W > 0, so that it is moving away from the Galactic plane.

In this section we will examine the rotation of the Milky Way. We start with the determination of the velocity components of the Sun. Then we will consider the rotation curve of the Galaxy, which describes the rotational velocity V (R) as a function of the distance R from the Galactic center. We will find the intriguing result that the velocity V does not decline towards large distances, but that it virtually remains constant. Because this result is of extraordinary importance, we will discuss the methods needed to derive it in some detail.

2.4.1 Determination of the velocity of the Sun

Local standard of rest. To link local measurements to the Galactic coordinate system (R, θ, z), the local standard of rest is defined. It is a fictitious rest-frame in which velocities are measured. For this purpose, we consider a point that is located today at the position of the Sun and that moves along a perfectly circular orbit in the plane of the Galactic disk. The velocity components in the LSR are then by definition,

$\displaystyle\begin{array}{rcl} \fbox{$U_{\mathrm{LSR}} \equiv 0\;, V _{\mathrm{LSR}} \equiv V _{0}\;, W_{\mathrm{LSR}} \equiv 0$}\;,& &{}\end{array}$

(2.49)

with V ₀ ≡ V (R ₀) being the orbital velocity at the location of the Sun. Although the LSR changes over time, the time-scale of this change is so large (the orbital period is ∼ 230 × 10⁶ yr) that this effect is negligible.

Peculiar velocity. The velocity of an object relative to the LSR is called its peculiar velocity. It is denoted by ${\boldsymbol v}$ , and its components are given as

$\displaystyle\begin{array}{rcl} \fbox{$\begin{array}{lll} {\boldsymbol v}& \equiv (u,v,w) = (U - U_{\mathrm{LSR}},V - V _{\mathrm{LSR}},W - W_{\mathrm{LSR}}) \\ & = (U,V - V _{0},W)\;. \end{array} $}& &{}\end{array}$

(2.50)

The velocity of the Sun relative to the LSR is denoted by ${\boldsymbol v}_{\odot }$ . If ${\boldsymbol v}_{\odot }$ is known, any velocity measured relative to the Sun can be converted into a velocity relative to the LSR: let $\varDelta {\boldsymbol v}$ be the velocity of a star relative to the Sun, which is directly measurable using the methods discussed in Sect. 2.2, then the peculiar velocity of this star is

$\displaystyle{ {\boldsymbol v} ={\boldsymbol v}_{\odot } +\varDelta {\boldsymbol v}\;. }$

(2.51)

Peculiar velocity of the Sun. We consider now an ensemble of stars in the immediate vicinity of the Sun, and assume the Galaxy to be axially symmetric and stationary. Under these assumptions, the number of stars that move outwards to larger radii R equals the number of stars moving inwards. Likewise, as many stars move upwards through the Galactic plane as downwards. If these conditions are not satisfied, the assumption of a stationary distribution would be violated. The mean values of the corresponding peculiar velocity components must therefore vanish,

$\displaystyle{ \left \langle u\right \rangle = 0\;,\quad \left \langle w\right \rangle = 0\;, }$

(2.52)

where the brackets denote an average over the ensemble considered. The analog argument is not valid for the v component because the mean value of v depends on the distribution of the orbits: if only circular orbits in the disk existed (with the same orientation as that of the Sun), we would also have $\left \langle v\right \rangle = 0$ (this is trivial, since then all stars would have v = 0), but this is not the case. From a statistical consideration of the orbits in the framework of stellar dynamics, one deduces that $\left \langle v\right \rangle$ is closely linked to the radial velocity dispersion of the stars: the larger it is, the more $\left \langle v\right \rangle$ deviates from zero. One finds that

$\displaystyle{ \left \langle v\right \rangle = -C\left \langle u^{2}\right \rangle \;, }$

(2.53)

where C is a positive constant that depends on the density distribution and on the local velocity distribution of the stars. The sign in (2.53) follows from noting that a circular orbit has a higher tangential velocity than elliptical orbits, which in addition have a non-zero radial component. Equation (2.53) expresses the fact that the mean rotational velocity of a stellar population around the Galactic center deviates from the corresponding circular orbit velocity, and that the deviation is stronger for a larger radial velocity dispersion. This phenomenon is also known as asymmetric drift. From the mean of (2.51) over the ensemble considered and by using (2.52) and (2.53), one obtains

$\displaystyle{ \fbox{${\boldsymbol v}_{\odot } = \left (-\left \langle \varDelta u\right \rangle,-C\left \langle u^{2}\right \rangle -\left \langle \varDelta v\right \rangle,-\left \langle \varDelta w\right \rangle \right )$}\;. }$

(2.54)

One still needs to determine the constant C in order to make use of this relation. This is done by considering different stellar populations and measuring $\left \langle u^{2}\right \rangle$ and $\left \langle \varDelta v\right \rangle$ separately for each of them. If these two quantities are then plotted in a diagram (see Fig. 2.23), a linear relation is obtained, as expected from (2.53). The slope C can be determined directly from this diagram. Furthermore, from the intersection with the $\left \langle \varDelta v\right \rangle$ -axis, $v_{\odot }$ is readily read off. The other velocity components in (2.54) follow by simply averaging, yielding the result:

$\displaystyle\begin{array}{rcl} \fbox{${\boldsymbol v}_{\odot } = (-10,5,7)\,\mathrm{km/s}$}\;.& &{}\end{array}$

(2.55)

Hence, the Sun is currently moving inwards, upwards, and faster than it would on a circular orbit at its location. We have therefore determined ${\boldsymbol v}_{\odot }$ , so we are now able to analyze any measured stellar velocities relative to the LSR. However, we have not yet discussed how V ₀, the rotational velocity of the LSR itself, is determined.

Velocity dispersion of stars. The dispersion of the stellar velocities relative to the LSR can now be determined, i.e., the mean square deviation of their velocities from the velocity of the LSR. For young stars (A stars, for example), this dispersion happens to be small. For older K giants it is larger, and is larger still for old, metal-poor red dwarf stars. We observe a very well-defined velocity-metallicity relation which, when combined with the age-metallicity relation, suggests that the oldest stars have the highest peculiar velocities. This effect is observed in all three coordinates and is in agreement with the relation between the age of a stellar population and its scale-height (discussed in Sect. 2.3.1), the latter being linked to the velocity dispersion via σ _z .

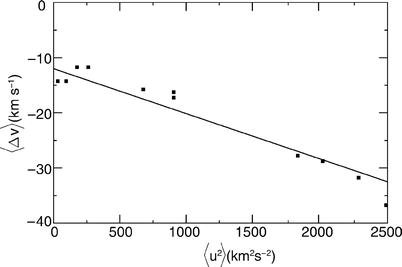
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig23_HTML.jpg

Fig. 2.23

The velocity components $\left \langle \varDelta v\right \rangle = \left \langle v\right \rangle - v_{\odot }$ are plotted against $\left \langle u^{2}\right \rangle$ for stars in the Solar neighborhood. Because of the linear relation, v _⊙ can be read off from the intersection with the x-axis, and C from the slope. Adopted from B.W. Carroll & D.A. Ostlie 1996, Introduction to Modern Astrophysics, Addison-Wesley

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig24_HTML.jpg

Fig. 2.24

The motion of the Sun around the Galactic center is reflected in the asymmetric drift: while young stars in the Solar vicinity have velocities very similar to the Solar velocity, i.e., small relative velocities, members of other populations (and of other Milky Way components) have different velocities—e.g., for halo objects $v = -220\,\mathrm{km/s}$ on average. Thus, different velocity ellipses show up in a (u − v)-diagram. Adopted from B.W. Carroll & D.A. Ostlie 1996, Introduction to Modern Astrophysics, Addison-Wesley

Asymmetric drift. If one considers high-velocity stars, only a few are found that have v > 65 km∕s and which are thus moving much faster around the Galactic center than the LSR. However, quite a few stars are found that have $v <-250\,\mathrm{km/s}$ , so their orbital velocity is opposite to the direction of rotation of the LSR. Plotted in a (u − v)-diagram, a distribution is found which is narrowly concentrated around $u = 0\,\mathrm{km/s} = v$ for young stars, as already mentioned above, and which gets increasingly wider for older stars. For the oldest stars, which belong to the halo population, one obtains a circular envelope with its center located at $u = 0\,\mathrm{km/s}$ and $v \approx -220\,\mathrm{km/s}$ (see Fig. 2.24). If we assume that the Galactic halo, to which these high-velocity stars belong, does not rotate (or only very slowly), this asymmetry in the v-distribution can only be caused by the rotation of the LSR. The center of the envelope then has to be at − V ₀. This yields the orbital velocity of the LSR

$\displaystyle{ \fbox{$V _{0} \equiv V (R_{0}) = 220\,\mathrm{km/s}$}\;. }$

(2.56)

Knowing this velocity, we can then compute the mass of the Galaxy inside the Solar orbit. A circular orbit is characterized by an equilibrium between centrifugal and gravitational acceleration, $V ^{2}/R = GM(<R)/R^{2}$ , so that

$\displaystyle{ \fbox{$M(<R_{0}) = \frac{V _{0}^{2}R_{0}} {G} = 8.8 \times 10^{10}\,M_{ \odot }$}\;. }$

(2.57)

Furthermore, for the orbital period of the LSR, which is similar to that of the Sun, one obtains

$\displaystyle{ \fbox{$P = \frac{2\pi R_{0}} {V _{0}} = 230 \times 10^{6}\,\mathrm{yr}$}\;. }$

(2.58)

Hence, during the lifetime of the Solar System, estimated to be ∼ 4. 6 × 10⁹ yr, it has completed about 20 orbits around the Galactic center.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig25_HTML.jpg

Fig. 2.25

Geometric derivation of the formalism of differential rotation:

$\displaystyle\begin{array}{rcl} v_{\mathrm{r}}& =& v_{\mathrm{r}}^{{\ast}}- v_{\mathrm{ r}}^{\odot } = v_{ {\ast}}\sin \ell^{{\ast}}- v_{ \odot }\sin \ell\;, {}\\ v_{\mathrm{t}}& =& v_{\mathrm{t}}^{{\ast}}- v_{\mathrm{ t}}^{\odot } = v_{ {\ast}}\cos \ell^{{\ast}}- v_{ \odot }\cos \ell\;. {}\\ \end{array}$

One has:

$\displaystyle\begin{array}{rcl} \frac{\sin \ell} {R} = \frac{\sin (\pi -\ell^{{\ast}})} {R_{0}} = \frac{\sin \ell^{{\ast}}} {R_{0}}\;,& & {}\\ R\cos \ell^{{\ast}} + D = R_{ 0}\cos \ell\;,& & {}\\ \end{array}$

which implies

$\displaystyle\begin{array}{rcl} v_{\mathrm{r}}& =& R_{0}\left (\frac{v_{{\ast}}} {R} -\frac{v_{\odot }} {R_{0}}\right )\sin \ell {}\\ & =& (\varOmega -\varOmega _{0})R_{0}\sin \ell\;, {}\\ v_{\mathrm{t}}& =& R_{0}\left (\frac{v_{{\ast}}} {R} -\frac{v_{\odot }} {R_{0}}\right )\cos \ell - D\frac{v_{{\ast}}} {R} {}\\ & =& (\varOmega -\varOmega _{0})R_{0}\cos \ell -\varOmega D\;. {}\\ \end{array}$

2.4.2 The rotation curve of the Galaxy

From observations of the velocity of stars or gas around the Galactic center, the rotational velocity V can be determined as a function of the distance R from the Galactic center. In this section, we will describe methods to determine this rotation curve and discuss the result.

Decomposition of rotational velocity. We consider an object at distance R from the Galactic center which moves along a circular orbit in the Galactic plane, has a distance D from the Sun, and is located at a Galactic longitude ℓ (see Fig. 2.4.1). In a Cartesian coordinate system with the Galactic center at the origin, the positional and velocity vectors (we only consider the two components in the Galactic plane because we assume a motion in the plane) are given by

$\displaystyle{{\boldsymbol r} = R\left (\begin{array}{c} \sin \theta \\ \cos \theta \end{array} \right )\;,\quad {\boldsymbol V } =\dot{{\boldsymbol r}} = V (R)\left (\begin{array}{c} \cos \theta \\ -\sin \theta \end{array} \right )\;,}$

where θ denotes the angle between the Sun and the object as seen from the Galactic center. From the geometry shown in Fig. 2.4.1 it follows that

$\displaystyle{{\boldsymbol r} = \left (\begin{array}{c} D\,\sin \ell\\ R_{0 } - D\,\cos \ell \end{array} \right )\;.}$

If we now identify the two expressions for the components of ${\boldsymbol r}$ , we obtain

$\displaystyle{\sin \theta = (D/R)\sin \ell\quad,\quad \cos \theta = (R_{0}/R) - (D/R)\cos \ell\;.}$

If we disregard the difference between the velocities of the Sun and the LSR we get ${\boldsymbol V }_{\odot }\approx {\boldsymbol V }_{\mathrm{LSR}} = (V _{0},0)$ in this coordinate system. Thus the relative velocity between the object and the Sun is, in Cartesian coordinates,

$\displaystyle{\varDelta {\boldsymbol V } ={\boldsymbol V }-{\boldsymbol V }_{\odot } = \left (\begin{array}{c} V \,(R_{0}/R) - V \,(D/R)\cos \ell - V _{0} \\ - V \,(D/R)\sin \ell \end{array} \right )\;.}$

With the angular velocity defined as

$\displaystyle{ \varOmega (R) = \frac{V (R)} {R} \;, }$

(2.59)

we obtain for the relative velocity

$\displaystyle{\varDelta {\boldsymbol V } = \left (\begin{array}{c} R_{0}(\varOmega -\varOmega _{0}) -\varOmega \, D\,\cos \ell \\ - D\,\varOmega \,\sin \ell \end{array} \right )\;,}$

where $\varOmega _{0} = V _{0}/R_{0}$ is the angular velocity of the Sun. The radial and tangential velocities of this relative motion then follow by projection of $\varDelta {\boldsymbol V }$ along the direction parallel or perpendicular, respectively, to the separation vector,

$\displaystyle\begin{array}{rcl} \fbox{$v_{\mathrm{r}} =\varDelta {\boldsymbol V } \cdot \left (\begin{array}{c} \sin \ell\\ -\cos \ell\end{array} \right ) = (\varOmega -\varOmega _{ 0})R_{0}\sin \ell$}\;,& &{}\end{array}$

(2.60)

$\displaystyle\begin{array}{rcl} \fbox{$v_{\mathrm{t}} =\varDelta {\boldsymbol V } \cdot \left (\begin{array}{c} \cos \ell\\ \sin \ell \end{array} \right ) = (\varOmega -\varOmega _{0})R_{0}\cos \ell -\varOmega \, D$}\;.& &{}\end{array}$

(2.61)

A purely geometric derivation of these relations is given in Fig. 2.4.1.

Rotation curve near R ₀ , Oort constants. Using (2.60) one can derive the angular velocity by means of measuring v _r, but not the radius R to which it corresponds. Therefore, by measuring the radial velocity alone Ω(R) cannot be determined. If one measures v _r and, in addition, the proper motion $\mu = v_{\mathrm{t}}/D$ of stars, then Ω and D can be determined from the equations above, and from D and ℓ one obtains $R = \sqrt{R_{0 }^{2 } + D^{2 } - 2R_{0 } D\cos \ell}$ . The effects of extinction prohibits the use of this method for large distances D, since we have considered objects in the Galactic disk. For small distances D ≪ R ₀, which implies $\vert R - R_{0}\vert \ll R_{0}$ , we can make a local approximation by evaluating the expressions above only up to first order in $(R - R_{0})/R_{0}$ . In this linear approximation we get

$\displaystyle{ \varOmega -\varOmega _{0} \approx \left ( \frac{\mathrm{d}\varOmega } {\mathrm{d}R}\right )_{\vert R_{0}}(R - R_{0})\;, }$

(2.62)

where the derivative has to be evaluated at R = R ₀. Hence

$\displaystyle{v_{\mathrm{r}} = (R - R_{0})\left ( \frac{\mathrm{d}\varOmega } {\mathrm{d}R}\right )_{\vert R_{0}}R_{0}\sin \ell\;,}$

and furthermore, with (2.59),

$\displaystyle{R_{0}\left ( \frac{\mathrm{d}\varOmega } {\mathrm{d}R}\right )_{\vert R_{0}} = \frac{R_{0}} {R} \left [\left (\frac{\mathrm{d}V } {\mathrm{d}R}\right )_{\vert R_{0}} -\frac{V } {R}\right ] \approx \left (\frac{\mathrm{d}V } {\mathrm{d}R}\right )_{\vert R_{0}} -\frac{V _{0}} {R_{0}} \;,}$

in zeroth order in $(R - R_{0})/R_{0}$ . Combining the last two equations yields

$\displaystyle{ v_{\mathrm{r}} = \left [\left (\frac{\mathrm{d}V } {\mathrm{d}R}\right )_{\vert R_{0}} -\frac{V _{0}} {R_{0}} \right ](R - R_{0})\sin \ell\;; }$

(2.63)

in analogy to this, we obtain for the tangential velocity

$\displaystyle{ v_{\mathrm{t}} = \left [\left (\frac{\mathrm{d}V } {\mathrm{d}R}\right )_{\vert R_{0}} -\frac{V _{0}} {R_{0}} \right ](R - R_{0})\cos \ell -\varOmega _{0}\,D\;. }$

(2.64)

For $\vert R - R_{0}\vert \ll R_{0}$ it follows that R ₀ − R ≈ Dcosℓ; if we insert this into (2.63) and (2.64) we get

$\displaystyle{ \fbox{$v_{\mathrm{r}} \approx A\,D\,\sin 2\ell\;\;, v_{\mathrm{t}} \approx A\,D\,\cos 2\ell + B\,D$}\;, }$

(2.65)

where A and B are the Oort constants

$\displaystyle\begin{array}{rcl} \fbox{$\begin{array}{cc} A&:= -\frac{1} {2}\left [\left (\frac{\mathrm{d}V } {\mathrm{d}R}\right )_{\vert R_{0}} -\frac{V _{0}} {R_{0}} \right ]\;, \\ B &:= -\frac{1} {2}\left [\left (\frac{\mathrm{d}V } {\mathrm{d}R}\right )_{\vert R_{0}} + \frac{V _{0}} {R_{0}} \right ]\;. \end{array} $}& &{}\end{array}$

(2.66)

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig26_HTML.jpg

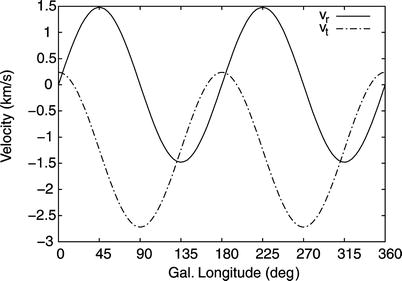
Fig. 2.26

The radial velocity v _r of stars at a fixed distance D is proportional to sin2ℓ; the tangential velocity v _t is a linear function of cos2ℓ. From the amplitude of the oscillating curves and from the mean value of v _t the Oort constants A and B can be derived, respectively [see (2.65)]

The radial and tangential velocity fields relative to the Sun show a sine curve with period π, where v _t and v _r are phase-shifted by π∕4. This behavior of the velocity field in the Solar neighborhood is indeed observed (see Fig. 2.26). By fitting the data for v _r(ℓ) and v _t(ℓ) for stars of equal distance D one can determine A and B, and thus

$\displaystyle\begin{array}{rcl} \fbox{$\varOmega _{0} = \frac{V _{0}} {R_{0}} = A - B, \left (\frac{\mathrm{d}V } {\mathrm{d}R}\right )_{\vert R_{0}} = -(A + B)$}\:.& &{}\end{array}$

(2.67)

The Oort constants thus yield the angular velocity of the Solar orbit and its derivative, and therefore the local kinematical information. If our Galaxy was rotating rigidly so that Ω was independent of the radius, A = 0 would follow. But the Milky Way rotates differentially, i.e., the angular velocity depends on the radius. Measurements yield the following values for A and B,

$\displaystyle\begin{array}{rcl} \fbox{$\begin{array}{cc} A = \left (14.8 \pm 0.8\right )\,\mathrm{km}\,\mathrm{s}^{-1}\,\mathrm{kpc}^{-1}\;,\;\; \\ B = \left (-12.4 \pm 0.6\right )\,\mathrm{km}\,\mathrm{s}^{-1}\,\mathrm{kpc}^{-1}\;. \end{array} $}& &{}\end{array}$

(2.68)

Fig. 2.27

The ISM is optically thin for 21 cm radiation, and thus we receive the 21 cm emission of Hi regions from everywhere in the Galaxy. Due to the motion of an Hi cloud relative to us, the wavelength is shifted. This can be used to measure the radial velocity of the cloud. With the assumption that the gas is moving on a circular orbit around the Galactic center, one expects that for the cloud in the tangent point (cloud 4), the full velocity is projected along the line-of-sight so that this cloud will therefore have the largest radial velocity. If the distance of the Sun to the Galactic center is known, the velocity of a cloud and its distance from the Galactic center can then be determined. Adopted from B.W. Carroll & D.A. Ostlie 1996, Introduction to Modern Astrophysics, Addison-Wesley

Galactic rotation curve for R < R ₀ ; tangent point method. To measure the rotation curve for radii that are significantly smaller than R ₀, one has to turn to large wavelengths due to extinction in the disk. Usually the 21 cm emission line of neutral hydrogen is used, which can be observed over large distances, or the emission of CO in molecular gas. These gas components are found throughout the disk and are strongly concentrated towards the plane. Furthermore, the radial velocity can easily be measured from the Doppler effect. However, since the distance to a hydrogen cloud cannot be determined directly, a method is needed to link the measured radial velocities to the distance of the gas from the Galactic center. For this purpose the tangent point method is used.

Consider a line-of-sight at fixed Galactic longitude ℓ, with cosℓ > 0 (thus ‘inwards’). The radial velocity v _r along this line-of-sight for objects moving on circular orbits is a function of the distance D, according to (2.60). If Ω(R) is a monotonically decreasing function, v _r attains a maximum where the line-of-sight is tangent to the local orbit, and thus its distance R from the Galactic center attains the minimum value R _min. This is the case at

$\displaystyle{ D = R_{0}\,\cos \ell\quad,\quad R_{\mathrm{min}} = R_{0}\,\sin \ell\; }$

(2.69)

(see Fig. 2.27). The maximum radial velocity there, according to (2.60), is

$\displaystyle\begin{array}{rcl} v_{\mathrm{r,max}} = \left [\varOmega (R_{\mathrm{min}}) -\varOmega _{0}\right ]\,R_{0}\,\sin \ell = V (R_{\mathrm{min}}) - V _{0}\,\sin \ell\;,& &{}\end{array}$

(2.70)

so that from the measured value of v _r,max as a function of direction ℓ, the rotation curve inside R ₀ can be determined,

$\displaystyle{ \fbox{$V (R) = \left ( \frac{R} {R_{0}}\right )V _{0} + v_{\mathrm{r,max}}(\sin \ell= R/R_{0})$}\;. }$

(2.71)

In the optical regime of the spectrum this method can only be applied locally, i.e., for small D, due to extinction. This is the case if one observes in a direction nearly tangential to the orbit of the Sun, i.e., if $0 <\pi /2-\ell\ll 1$ or $0 <\ell -3\pi /2 \ll 1$ , or | sinℓ | ≈ 1, so that $R_{0} - R_{\mathrm{min}} \ll R_{0}$ . In this case we get, to first order in (R ₀ − R _min), using (2.69),

$\displaystyle\begin{array}{rcl} V (R_{\mathrm{min}})& \approx & V _{0} + \left (\frac{\mathrm{d}V } {\mathrm{d}R}\right )_{\vert R_{0}}\left (R_{\mathrm{min}} - R_{0}\right ) \\ & =& V _{0} -\left (\frac{\mathrm{d}V } {\mathrm{d}R}\right )_{\vert R_{0}}R_{0}\,(1-\sin \ell)\;,{}\end{array}$

(2.72)

so that with (2.70)

$\displaystyle\begin{array}{rcl} \fbox{$\begin{array}{cc} v_{\mathrm{r,max}} & = \left [V _{0} -\left (\frac{\mathrm{d}V } {\mathrm{d}R}\right )_{\vert R_{0}}R_{0}\right ](1-\sin \ell) \\ & = 2\,A\,R_{0}\,(1-\sin \ell)\;, \end{array} $}& &{}\end{array}$

(2.73)

where (2.66) was used in the last step. This relation can also be used for determining the Oort constant A.

To determine V (R) for smaller R by employing the tangent point method, we have to observe in wavelength regimes in which the Galactic plane is transparent, using radio emission lines of gas. In Fig. 2.27, a typical intensity profile of the 21 cm line along a line-of-sight is sketched; according to the Doppler effect this can be converted directly into a velocity profile using $v_{\mathrm{r}} = (\lambda -\lambda _{0})/\lambda _{0}$ . It consists of several maxima that originate in individual gas clouds. The radial velocity of each cloud is defined by its distance R from the Galactic center (if the gas follows the Galactic rotation), so that the largest radial velocity will occur for gas closest to the tangent point, which will be identified with v _r,max(ℓ). Figure 2.28 shows the observed intensity profile of the¹²CO line as a function of the Galactic longitude, from which the rotation curve for R < R ₀ can be read off.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig28_HTML.jpg

Fig. 2.28

¹²CO emission of molecular gas in the Galactic disk. For each ℓ, the intensity of the emission in the ℓ − v _r plane is plotted, integrated over the range − 2^∘ ≤ b ≤ 2^∘ (i.e., very close to the middle of the Galactic plane). Since v _r depends on the distance along each line-of-sight, characterized by ℓ, this diagram contains information on the rotation curve of the Galaxy as well as on the spatial distribution of the gas. The maximum velocity at each ℓ is rather well defined and forms the basis for the tangent point method. Source: P. Englmaier & O. Gerhard 1999, Gas dynamics and large-scale morphology of the Milky Way galaxy, MNRAS 304, 512, p. 514, Fig. 1. Reproduced by permission of Oxford University Press on behalf of the Royal Astronomical Society

Fig. 2.29

Rotation curve of the Milky Way. Inside the “Solar circle”, that is at R < R ₀, the radial velocity is determined quite accurately using the tangent point method; the measurements outside have larger uncertainties. Source: D. Clemens 1985, Massachusetts-Stony Brook Galactic plane CO survey—The Galactic disk rotation curve ApJ 295, 422, p. 429, Fig. 3. ©AAS. Reproduced with permission

With the tangent point method, applied to the 21 cm line of neutral hydrogen or to radio emission lines of molecular gas, the rotation curve of the Galaxy inside the Solar orbit, i.e., for R < R ₀, can be measured.

Rotation curve for R > R ₀ . The tangent point method cannot be applied for R > R ₀ because for lines-of-sight at $\pi /2 <\ell<3\pi /2$ , the radial velocity v _r attains no maximum. In this case, the line-of-sight is nowhere parallel to a circular orbit.

Measuring V (R) for R > R ₀ requires measuring v _r for objects whose distance can be determined directly, e.g., Cepheids, for which the period-luminosity relation (Sect. 2.2.7) is used, or O- and B-stars in Hii-regions. With ℓ and D known, R can then be calculated, and with (2.60) we obtain Ω(R) or V (R), respectively. Any object with known D and v _r thus contributes one data point to the Galactic rotation curve. Since the distance estimates of individual objects are always affected by uncertainties, the rotation curve for large values of R is less accurately known than that inside the Solar circle. Recent measurements of blue horizontal-branch stars within the outer halo of the Milky Way by SDSS yielded an estimate of the rotation curve out to r ∼ 60 kpc. The situation will improve dramatically once the results from Gaia will become available: Gaia will measure distances via trigonometric parallaxes, and proper motions of many star outside the Solar circle.

It turns out that the rotation curve for R > R ₀ does not decline outwards (see Fig. 2.29) as we would expect from the distribution of visible matter in the Milky Way. Both the stellar density and the gas density of the Galaxy decline exponentially for large R—e.g., see (2.35). This steep radial decline of the visible matter density should imply that M(R), the mass inside R, is nearly constant for R ≳ R ₀, from which a velocity profile like $V \propto R^{-1/2}$ would follow, according to Kepler’s law. However, this is not the case: V (R) is virtually constant for R > R ₀, indicating that M(R) ∝ R. In fact, a small decrease to about 180 km∕s at R = 60 kpc was estimated, corresponding to a total mass of (4. 0 ± 0. 7) × 10¹¹ M _⊙ enclosed within the inner 60 kpc, but this decrease is much smaller than expected from Keplerian rotation. In order to get an almost constant rotational velocity of the Galaxy, much more matter has to be present than we observe in gas and stars.

The Milky Way contains, besides stars and gas, an additional component of matter that dominates the mass at R ≳ R ₀. Its presence is known only by its gravitational effect, since it has not been observed directly yet, neither in emission nor in absorption. Hence, it is called dark matter.

In Sect. 3.3.4 we will see that this is a common phenomenon. The rotation curves of spiral galaxies are flat up to the maximum radius at which they can be measured; spiral galaxies contain dark matter. A better way of phrasing is would be to say that the visible galaxy is embedded in a dark matter halo, since the total mass of the Milky Way (and other spiral galaxies) is dominated by dark matter.

2.4.3 The gravitational potential of the Galaxy

We have little direct indications about the spatial extent of the dark matter halo, and thus its total mass, because at large radii R there are not many luminous objects whose orbit we can use to measure the rotation curve out there. From the motion of satellite galaxies, such as the Magellanic Clouds, one gets mass estimates at larger distances, but with less accuracy. For example, the mass inside of 100 kpc is estimated to be $(7 \pm 2.5) \times 10^{11}M_{\odot }$ from such satellite motions. Furthermore, it is largely unknown whether this halo is approximately spherical or deviates significantly from sphericity, being either oblate or prolate. The stellar streams that we discussed in Sect. 2.3.6 above can in principle be used to constrain the axis ratio of the total matter distribution out to large radii—if the gravitational potential of the Milky Way was spherical, the streams would lie in a single orbital plane, so that deviations from it can be used to probe the axis ratio of the potential. However, currently the results from such studies are burdened with uncertainties, and different results are obtained from different studies.

The nature of dark matter is thus far unknown; in principle, we can distinguish two totally different kinds of dark matter candidates:

Astrophysical dark matter, consisting of compact objects—e.g., faint stars like white dwarfs, brown dwarfs, black holes, etc. Such objects were assigned the name MACHOs, which stands for ‘MAssive Compact Halo Objects’.
Particle physics dark matter, consisting of elementary particles which thus far have escaped detection in laboratories.

Although the origin of astrophysical dark matter would be difficult to understand (not least because of the baryon abundance in the Universe—see Sect. 4.4.5—and because of the metal abundance in the ISM), a direct distinction between the two alternatives through observation would be of great interest. In the following section we will describe a method which is able to probe whether the dark matter in our Galaxy consists of MACHOs.

2.5 The Galactic microlensing effect: The quest for compact dark matter

In 1986, Bohdan Paczyński proposed to test the possible presence of MACHOs by performing microlensing experiments. As we will soon see, this was a daring idea at that time, but since then such experiments have been carried out. In this section we will mainly summarize and discuss the results of these searches for MACHOs. We will start with a description of the microlensing effect and then proceed with its specific application to the search for MACHOs.

2.5.1 The gravitational lensing effect I

Einstein’s deflection angle. Light, just like massive particles, is deflected in a gravitational field. This is one of the specific predictions by Einstein’s theory of gravity, General Relativity. Quantitatively it predicts that a light beam which passes a point mass M at a distance ξ is deflected by an angle $\hat{\alpha }$ , which amounts to

$\displaystyle{ \fbox{$\hat{\alpha } = \frac{4\,G\,M} {c^{2}\,\xi } $}\;. }$

(2.74)

The deflection law (2.74) is valid as long as $\hat{\alpha }\ll 1$ , which is the case for weak gravitational fields. If we now set $M = M_{\odot }$ , $\xi = R_{\odot }$ in the foregoing equation, we obtain

$\displaystyle{ \fbox{$\hat{\alpha }_{\odot }\approx 1.\!\!^{{\prime\prime}}74$} }$

for the light deflection at the limb of the Sun. This deflection of light was measured during a Solar eclipse in 1919 from the shift of the apparent positions of stars close to the shaded Solar disk. Its agreement with the value predicted by Einstein made him world-famous over night, because this was the first real and challenging test of General Relativity. Although the precision of the measured value back then was only ∼ 30 %, it was sufficient to confirm Einstein’s theory. By now the law (2.74) has been measured in the Solar System with a relative precision of about 5 × 10⁻⁴, and Einstein’s prediction has been confirmed.

Not long after the discovery of gravitational light deflection at the Sun, the following scenario was considered. If the deflection was sufficiently strong, light from a very distant source could be visible at two positions in the sky: one light ray could pass a mass concentration, located between us and the source, ‘to the right’, and the second one ‘to the left’, as sketched in Fig. 2.30. The astrophysical consequence of this gravitational light deflection is also called the gravitational lens effect. We will discuss various aspects of the lens effect in the course of this book, and we will review its astrophysical applications.

Fig. 2.30

Sketch of a gravitational lens system. If a sufficiently massive mass concentration is located between us and a distant source, it may happen that we observe this source at two different positions on the sphere. Source: J. Wambsganss 1998, Gravitational Lensing in Astronomy, Living Review in Relativity 1, 12, Fig. 2. ©Max Planck Society and the author; Living Reviews in Relativity, published by the Max Planck Institute for Gravitational Physics (Albert Einstein Institute), Germany

The Sun is not able to cause multiple images of distant sources. The maximum deflection angle $\hat{\alpha }_{\odot }$ is much smaller than the angular radius of the Sun, so that two beams of light that pass the Sun to the left and to the right cannot converge by light deflection at the position of the Earth. Given its radius, the Sun is too close to produce multiple images, since its angular radius is (far) larger than the deflection angle $\hat{\alpha }_{\odot }$ . However, the light deflection by more distant stars (or other massive celestial bodies) can produce multiple images of sources located behind them.

Fig. 2.31

Geometry of a gravitational lens system. Consider a source to be located at a distance D _s from us and a mass concentration at distance D _d. An optical axis is defined that connects the observer and the center of the mass concentration; its extension will intersect the so-called source plane, a plane perpendicular to the optical axis at the distance of the source. Accordingly, the lens plane is the plane perpendicular to the line-of-sight to the mass concentration at distance D _d from us. The intersections of the optical axis and the planes are chosen as the origins of the respective coordinate systems. Let the source be at the location ${\boldsymbol \eta }$ in the source plane; a light beam that encloses an angle ${\boldsymbol \theta }$ to the optical axis intersects the lens plane at the point ${\boldsymbol \xi }$ and is deflected by an angle $\hat{{\boldsymbol \alpha }}({\boldsymbol \xi })$ . All these quantities are two-dimensional vectors. The condition that the source is observed in the direction ${\boldsymbol \theta }$ is given by the lens equation (2.77) which follows from the theorem of intersecting lines. Adapted from: P. Schneider, J. Ehlers & E.E. Falco 1992, Gravitational Lenses, Springer-Verlag

Lens geometry. The geometry of a gravitational lens system is depicted in Fig. 2.31. We consider light rays from a source at distance D _s from us that pass a mass concentration (called a lens or deflector) at a separation ${\boldsymbol \xi }$ . The deflector is at a distance D _d from us. In Fig. 2.31 ${\boldsymbol \eta }$ denotes the true, two-dimensional position of the source in the source plane, and ${\boldsymbol \beta }$ is the true angular position of the source, that is the angular position at which it would be observed in the absence of light deflection,

$\displaystyle{ {\boldsymbol \beta }= \frac{{\boldsymbol \eta }} {D_{\mathrm{s}}}\;. }$

(2.75)

The position of the light ray in the lens plane is denoted by ${\boldsymbol \xi }$ , and ${\boldsymbol \theta }$ is the corresponding angular position,

$\displaystyle{ {\boldsymbol \theta }= \frac{{\boldsymbol \xi }} {D_{\mathrm{d}}}\;. }$

(2.76)

Hence, ${\boldsymbol \theta }$ is the observed position of the source on the sphere relative to the position of the ‘center of the lens’ which we have chosen as the origin of the coordinate system, ${\boldsymbol \xi }= 0$ . Like the position vectors ${\boldsymbol \xi }$ and ${\boldsymbol \eta }$ , the angles ${\boldsymbol \theta }$ and ${\boldsymbol \beta }$ are two-dimensional vectors, corresponding to the two directions on the sky. D _ds is the distance of the source plane from the lens plane. As long as the relevant distances are much smaller than the ‘radius of the Universe’ c∕H ₀, which is certainly the case within our Galaxy and in the Local Group, we have $D_{\mathrm{ds}} = D_{\mathrm{s}} - D_{\mathrm{d}}$ . However, this relation is no longer valid for cosmologically distant sources and lenses; we will come back to this issue in Sect. 4.3.3.

Lens equation. From Fig. 2.31 we can deduce the condition that a light ray from the source will reach us from the direction ${\boldsymbol \theta }$ (or ${\boldsymbol \xi }$ ),

$\displaystyle{ {\boldsymbol \eta }= \frac{D_{\mathrm{s}}} {D_{\mathrm{d}}}{\boldsymbol \xi } - D_{\mathrm{ds}}\hat{{\boldsymbol \alpha }}({\boldsymbol \xi })\;, }$

(2.77)

or, after dividing by D _s and using (2.75) and (2.76):

$\displaystyle{ {\boldsymbol \beta } = {\boldsymbol \theta } -\frac{D_{\mathrm{ds}}} {D_{\mathrm{s}}} \,\hat{{\boldsymbol \alpha }}(D_{\mathrm{d}}{\boldsymbol \theta })\;. }$

(2.78)

Due to the factor multiplying the deflection angle in (2.78), it is convenient to define the reduced deflection angle

$\displaystyle{ \fbox{${\boldsymbol \alpha }({\boldsymbol \theta }):= \frac{D_{\mathrm{ds}}} {D_{\mathrm{s}}} \,\hat{{\boldsymbol \alpha }}(D_{\mathrm{d}}{\boldsymbol \theta })$}\;, }$

(2.79)

so that the lens equation (2.78) attains the simple form

$\displaystyle{ \fbox{${\boldsymbol \beta } = {\boldsymbol \theta } -{\boldsymbol \alpha } ({\boldsymbol \theta })$}\;. }$

(2.80)

Multiple images of a source occur if the lens equation (2.80) has multiple solutions ${\boldsymbol \theta }_{i}$ for a (true) source position ${\boldsymbol \beta }$ —in this case, the source is observed at the positions ${\boldsymbol \theta }_{i}$ on the sphere.

The deflection angle ${\boldsymbol \alpha }({\boldsymbol \theta })$ depends on the mass distribution of the deflector. We will discuss the deflection angle for an arbitrary density distribution of a lens in Sect. 3.11. Here we will first concentrate on point masses, which is—in most cases—a good approximation for the lensing effect by stars.

For a point mass, we get—see (2.74)—

$\displaystyle{\left \vert {\boldsymbol \alpha }\right \vert ({\boldsymbol \theta }) = \frac{D_{\mathrm{ds}}} {D_{\mathrm{s}}} \,\frac{4\,G\,M} {c^{2}\,D_{\mathrm{d}}\,\vert {\boldsymbol \theta }\vert } \;,}$

or, if we account for the direction of the deflection (the deflection angle always points towards the point mass),

$\displaystyle{ \fbox{${\boldsymbol \alpha }({\boldsymbol \theta }) = \frac{4\,G\,M} {c^{2}} \, \frac{D_{\mathrm{ds}}} {D_{\mathrm{s}}\,D_{\mathrm{d}}}\, \frac{{\boldsymbol \theta }} {\vert {\boldsymbol \theta }\vert ^{2}}$}\;. }$

(2.81)

Explicit solution of the lens equation for a point mass. The lens equation for a point mass is simple enough to be solved analytically which means that for each source position ${\boldsymbol \beta }$ the respective image positions ${\boldsymbol \theta }_{i}$ can be determined. In (2.81), the left-hand side is an angle, whereas ${\boldsymbol \theta }/\vert {\boldsymbol \theta }\vert ^{2}$ is an inverse of an angle. Hence, the prefactor of this term must be the square of an angle, which is called the Einstein angle of the lens,

$\displaystyle{ \fbox{$\theta _{\mathrm{E}}:= \sqrt{\frac{4\,G\,M} {c^{2}} \, \frac{D_{\mathrm{ds}}} {D_{\mathrm{s}}\,D_{\mathrm{d}}}}$}\;; }$

(2.82)

thus the lens equation (2.80) for the point-mass lens with a deflection angle (2.81) can be written as

$\displaystyle{{\boldsymbol \beta }={\boldsymbol \theta } -\theta _{\mathrm{E}}^{2}\, \frac{{\boldsymbol \theta }} {\vert {\boldsymbol \theta }\vert ^{2}}\;.}$

Obviously, θ _E is a characteristic angle in this equation, so that for practical reasons we will use the scaling

$\displaystyle{{\boldsymbol y}:= \frac{{\boldsymbol \beta }} {\theta _{\mathrm{E}}}\quad;\quad {\boldsymbol x}:= \frac{{\boldsymbol \theta }} {\theta _{\mathrm{E}}}\;,}$

and the lens equation simplifies to

$\displaystyle\begin{array}{rcl} {\boldsymbol y} ={\boldsymbol x} - \frac{{\boldsymbol x}} {\left \vert {\boldsymbol x}\right \vert ^{2}}\;.& &{}\end{array}$

(2.83)

After multiplication with ${\boldsymbol x}$ , this becomes a quadratic equation, whose solutions are

$\displaystyle\begin{array}{rcl} {\boldsymbol x} = \frac{1} {2}\left (\left \vert {\boldsymbol y}\right \vert \pm \sqrt{4 + \left \vert {\boldsymbol y} \right \vert ^{2}}\right )\,\frac{{\boldsymbol y}} {\left \vert {\boldsymbol y}\right \vert }\;.& &{}\end{array}$

(2.84)

From this solution of the lens equation one can immediately draw a number of conclusions:

For each source position ${\boldsymbol y}\neq {\boldsymbol 0}$ , the lens equation for a point-mass lens has two solutions—any source is (formally, at least) imaged twice. The reason for this is the divergence of the deflection angle for θ → 0. This divergence does not occur in reality because of the finite geometric extent of the lens (e.g., the radius of the star), as the solutions are of course physically relevant only if $\xi = D_{\mathrm{d}}\theta _{\mathrm{E}}\vert {\boldsymbol x}\vert$ is larger than the radius of the star. We need to point out again that we explicitly exclude the case of strong gravitational fields such as the light deflection near a black hole or a neutron star, for which the equation for the deflection angle has to be modified, since there the gravitational field is no longer weak.
The two images ${\boldsymbol x}_{i}$ are collinear with the lens and the source. In other words, the observer, lens, and source define a plane, and light rays from the source that reach the observer are located in this plane as well. One of the two images is located on the same side of the lens as the source ( ${\boldsymbol x} \cdot {\boldsymbol y}> 0$ ), the second image is located on the other side—as is already indicated in Fig. 2.30.
If ${\boldsymbol y} = 0$ , so that the source is positioned exactly behind the lens, the full circle $\left \vert {\boldsymbol x}\right \vert = 1$ , or $\vert {\boldsymbol \theta }\vert =\theta _{\mathrm{E}}$ , is a solution of the lens equation (2.83)—the source is seen as a circular image. In this case, the source, lens, and observer no longer define a plane, and the problem becomes axially symmetric. Such a circular image is called an Einstein ring. Ring-shaped images have indeed been observed, as we will discuss in Sect. 3.11.3
The angular diameter of this ring is then 2θ _E. From the solution (2.84), one can easily see that the separation between the two images is about $\varDelta x = \left \vert {\boldsymbol x}_{1} -{\boldsymbol x}_{2}\right \vert \gtrsim 2$ (as long as $\left \vert {\boldsymbol y}\right \vert \gtrsim 1$ ), hence

$\displaystyle\begin{array}{rcl} \varDelta \theta \gtrsim 2\theta _{\mathrm{E}}\;;& & {}\\ \end{array}$

the Einstein angle thus specifies the characteristic image separation. Situations with $\left \vert {\boldsymbol y}\right \vert \gg 1$ , and hence angular separations significantly larger than 2θ _E, are astrophysically of only minor relevance, as will be shownbelow.

Magnification—the principle. Light beams are not only deflected as a whole, but they are also subject to differential deflection. For instance, those rays of a light beam (also called light bundle) that are closer to the lens are deflected more than rays at the other side of the beam. The differential deflection is an effect of the tidal component of the deflection angle; this is sketched in Fig. 2.32.

Fig. 2.32

Light beams are deflected differentially, leading to changes of the shape and the cross-sectional area of the beam. As a consequence, the observed solid angle subtended by the source, as seen by the observer, is modified by gravitational light deflection. In the example shown, the observed solid angle $\mathcal{A}_{\mathrm{I}}/D_{\mathrm{d}}^{2}$ is larger than the one subtended by the undeflected source, $\mathcal{A}_{\mathrm{S}}/D_{\mathrm{s}}^{2}$ —the image of the source is thus magnified. Source: P. Schneider, J. Ehlers & E.E. Falco 1992, Gravitational Lenses, Springer-Verlag

By differential deflection, the solid angle which the image of the source subtends on the sky changes. Let ω _s be the solid angle the source would subtend if no lens was present, and ω the observed solid angle of the image of the source in the presence of a deflector. Since gravitational light deflection is not linked to emission or absorption of radiation, the surface brightness (or specific intensity) is preserved. The flux of a source is given as the product of surface brightness and solid angle. Since the former of the two factors is unchanged by light deflection, but the solid angle changes, the observed flux of the source is modified. If S ₀ is the flux of the unlensed source and S the flux of an image of the source, then

$\displaystyle{ \fbox{$\mu:= \frac{S} {S_{0}} = \frac{\omega } {\omega _{\mathrm{s}}}$} }$

(2.85)

describes the change in flux that is caused by a magnification (or a diminution) of the image of a source. Obviously, the magnification is a purely geometrical effect.

Magnification for ‘small’ sources. For sources and images that are much smaller than the characteristic scale of the lens, the magnification μ is given by the differential area distortion of the lens mapping (2.80),

$\displaystyle\begin{array}{rcl} \fbox{$\mu = \left \vert \det \left (\frac{\partial {\boldsymbol \beta }} {\partial {\boldsymbol \theta }}\right )\right \vert ^{-1} \equiv \left \vert \det \left (\frac{\partial \beta _{i}} {\partial \theta _{j}}\right )\right \vert ^{-1}$}\;.& &{}\end{array}$

(2.86)

Hence for small sources, the ratio of solid angles of the lensed image and the unlensed source is described by the determinant of the local Jacobi matrix.¹⁴

The magnification can therefore be calculated for each individual image of the source, and the total magnification of a source, given by the ratio of the sum of the fluxes of the individual images and the flux of the unlensed source, is the sum of the magnifications for the individual images.

Magnification for the point-mass lens. For a point-mass lens, the magnifications for the two images (2.84) are

$\displaystyle\begin{array}{rcl} \mu _{\pm } = \frac{1} {4}\left ( \frac{y} {\sqrt{y^{2 } + 4}} + \frac{\sqrt{y^{2 } + 4}} {y} \pm 2\right )\;.& &{}\end{array}$

(2.87)

From this it follows that for the ‘+’-image μ ₊ > 1 for all source positions $y = \left \vert {\boldsymbol y}\right \vert$ , whereas the ‘−’-image can have magnification either larger or less than unity, depending on y. The magnification of the two images is illustrated in Fig. 2.33, while Fig. 2.34 shows the magnification for several different source positions y. For y ≫ 1, one has μ ₊ ≳ 1 and μ ₋ ∼ 0, from which we draw the following conclusion: if the source and lens are not sufficiently well aligned, the secondary image is strongly demagnified and the primary image has magnification very close to unity. For this reason, situations with y ≫ 1 are of little relevance since then essentially only one image is observed which has about the same flux as the unlensed source.

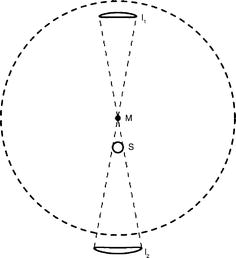
/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig33_HTML.jpg

Fig. 2.33

Illustration of the lens mapping by a point mass M. The unlensed source S and the two images I₁ and I₂ of the lensed source are shown. We see that the two images have a solid angle different from the unlensed source, and they also have a different shape. The dashed circle shows the Einstein radius of the lens. Source: B. Paczyński 1996, Gravitational Microlensing in the Local Group ARA&A 34, 419, p. 424. Reprinted, with permission, from the Annual Review of Astronomy & Astrophysics, Volume 34 ©1996 by Annual Reviews www.annualreviews.org

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig34_HTML.jpg

Fig. 2.34

Image of a circular source with a radial brightness profile—indicated by colors—for different relative positions of the lens and source. y decreases from left to right; in the rightmost figure y = 0 and an Einstein ring is formed. Source: J. Wambsganss 1998, Gravitational Lensing in Astronomy, Living Review in Relativity 1, 12, Fig. 20. ©Max Planck Society and the author; Living Reviews in Relativity, published by the Max Planck Institute for Gravitational Physics (Albert Einstein Institute), Germany

For y → 0, the two magnifications diverge, μ _± → ∞. The reason for this is purely geometric: in this case, out of a 0-dimensional point source a one-dimensional image, the Einstein ring, is formed. This divergence is not physical, of course, since infinite magnifications do not occur in reality. The magnifications remain finite even for y = 0, for two reasons. First, real sources have a finite extent, and for these the magnification is finite. Second, even if one had a point source, wave effects of the light (interference) would lead to a finite value of μ. The total magnification of a point source by a point-mass lens follows from the sum of the magnifications (2.87),

$\displaystyle{ \fbox{$\mu (y) =\mu _{+} +\mu _{-} = \frac{y^{2} + 2} {y\sqrt{y^{2 } + 4}}$}\;. }$

(2.88)

2.5.2 Galactic microlensing effect

After these theoretical considerations we will now return to the starting point of our discussion, employing the lensing effect as a potential diagnostic for dark matter in our Milky Way, if this dark matter were to consist of compact mass concentrations, e.g., very faint stars.

Image splitting. Considering a star in our Galaxy as the lens, (2.82) yields the Einstein angle

$\displaystyle\begin{array}{rcl} \fbox{$\theta _{\mathrm{E}} = 0.902\,\mathrm{mas}\left ( \frac{M} {M_{\odot }}\right )^{1/2}\left ( \frac{D_{\mathrm{d}}} {10\,\mathrm{kpc}}\right )^{-1/2}\left (1 -\frac{D_{\mathrm{d}}} {D_{\mathrm{s}}} \right )^{1/2}$}\;.& &{}\end{array}$

(2.89)

Since the angular separation Δ θ of the two images is about 2θ _E, the typical image splittings are about a milliarcsecond (mas) for lens systems including Galactic stars; such angular separations are as yet not observable with optical telescopes. This insight made Einstein believe in 1936, after he conducted a detailed quantitative analysis of gravitational lensing by point masses, that the lens effect will not be observable.¹⁵

Magnification. Bohdan Paczyński pointed out in 1986 that, although image splitting was unobservable, the magnification by the lens should nevertheless be measurable. To do this, we have to realize that the absolute magnification is observable only if the unlensed flux of the source is known—which is not the case, of course (for nearly all sources). However, the magnification, and therefore also the observed flux, changes with time by the relative motion of source, lens, and ourselves. Therefore, the flux is a function of time, caused by the time-dependent magnification.

Characteristic time-scale of the variation. Let v be a typical transverse velocity of the lens, then its angular velocity (or proper motion) is

$\displaystyle\begin{array}{rcl} \dot{\theta }= \frac{v} {D_{\mathrm{d}}} = 4.22\,\mathrm{mas}\,\mathrm{yr}^{-1}\left ( \frac{v} {200\,\mathrm{km/s}}\right )\left ( \frac{D_{\mathrm{d}}} {10\,\mathrm{kpc}}\right )^{-1}\;,& &{}\end{array}$

(2.90)

if we consider the source and the observer to be at rest. The characteristic time-scale of the variability is then given by

$\displaystyle\begin{array}{rcl} \fbox{$\begin{array}{cc} t_{\mathrm{E}}:= \frac{\theta _{\mathrm{E}}} {\dot{\theta }} & = 0.214\,\mathrm{yr}\left ( \frac{M} {M_{\odot }}\right )^{1/2}\left ( \frac{D_{\mathrm{d}}} {10\,\mathrm{kpc}}\right )^{1/2} \\ & \times \left (1 -\frac{D_{\mathrm{d}}} {D_{\mathrm{s}}} \right )^{1/2}\left ( \frac{v} {200\,\mathrm{km/s}}\right )^{-1}\;. \end{array} $}& &{}\end{array}$

(2.91)

This time-scale is of the order of a month for lenses with M ∼ M _⊙ and typical Galactic velocities. In the general case that source, lens, and observer are all moving, v has to be considered as an effective velocity. Alternatively, the motion of the source in the source plane can be considered.

The fact that t _E comes out to be a month for characteristic values of distances and velocities in our Galaxy is a fortunate coincidence, since it implies that these variations are in fact observable. If the time-scale was a factor ten times larger, the characteristic light curve would extend over several observing periods and include the annual gaps where the sources are not visible, making the detection of events much more difficult. If t _E was of order several years, the variability time-scale would be longer than the life-time of most projects in astrophysics. Conversely, it t _E was considerable shorter than a day, the variations would be difficult to record.

Light curves. In most cases, the relative motion can be considered linear, so that the position of the source in the source plane can be written as

$\displaystyle{{\boldsymbol \beta }={\boldsymbol \beta } _{0} +\dot{{\boldsymbol \beta }} (t - t_{0})\;.}$

Using the scaled position ${\boldsymbol y} ={\boldsymbol \beta } /\theta _{\mathrm{E}}$ , for $y = \left \vert {\boldsymbol y}\right \vert$ we obtain

$\displaystyle{ \fbox{$y(t) = \sqrt{p^{2 } + \left (\frac{t - t_{\mathrm{max } } } {t_{\mathrm{E}}} \right )^{2}}$}\;, }$

(2.92)

where p = y _min specifies the minimum distance from the optical axis, and t _max is the time at which y = p attains this minimum value, thus when the magnification $\mu =\mu (p) =\mu _{\mathrm{max}}$ is maximized. From this, and using (2.88), one obtains the light curve

$\displaystyle{ \fbox{$S(t) = S_{0}\,\mu (y(t)) = S_{0}\, \frac{y^{2}(t) + 2} {y(t)\,\sqrt{y^{2 } (t) + 4}}$}\;. }$

(2.93)

Fig. 2.35

Illustration of a Galactic microlensing event: In the upper panel a source (depicted by the open circles) moves behind a point-mass lens; for each source position two images of the source are formed, which are indicated by the black ellipses. Note that Fig. 2.33 shows the imaging properties for one of the source positions shown here. The identification of the corresponding image pair with the source position follows from the fact that, in projection, the source, the lens, and the two images are located on a straight line, which is indicated for one source position; this property follows from the collinearity of source and images mentioned in the text. The dashed circle represents the Einstein ring. In the middle panel, different trajectories of the source are shown, each characterized by the smallest projected separation p to the lens. The light curves resulting from these relative motions, which can be calculated using (2.93), are then shown in the bottom panel for different values of p. The smaller p is, the larger the maximum magnification will be, here measured in magnitudes. Source: B. Paczyński 1996, Gravitational Microlensing in the Local Group ARA&A 34, 419, p. 425, 426, 427. Reprinted, with permission, from the Annual Review of Astronomy & Astrophysics, Volume 34 ©1996 by Annual Reviews www.annualreviews.org

Examples for such light curves are shown in Fig. 2.35. They depend on only four parameters: the flux of the unlensed source S ₀, the time of maximum magnification t _max, the smallest distance of the source from the optical axis p, and the characteristic time scale t _E. All these values are directly observable in a light curve. One obtains t _max from the time of the maximum of the light curve, S ₀ is the flux that is measured for very large and small times, S ₀ = S(t → ±∞), or S ₀ ≈ S(t) for $\left \vert t - t_{\mathrm{max}}\right \vert \gg t_{\mathrm{E}}$ . Furthermore, p follows from the maximum magnification $\mu _{\mathrm{max}} = S_{\mathrm{max}}/S_{0}$ by inversion of (2.88), and t _E from the width of the light curve.

Only t _E contains information of astrophysical relevance, because the time of the maximum, the unlensed flux of the source, and the minimum separation p provide no information about the lens. Since $t_{\mathrm{E}} \propto \sqrt{M\,D_{\mathrm{d}}}/v$ , this time scale contains the combined information on the lens mass, the distances to the lens and the source, and the transverse velocity: Only the combination $t_{\mathrm{E}} \propto \sqrt{M\,D_{\mathrm{d}}}/v$ can be derived from the light curve, but not mass, distance, or velocity individually.

Paczyński’s idea can be expressed as follows: if the halo of our Milky Way consists (partially) of compact objects, a distant compact source should, from time to time, be lensed by one of these MACHOs and thus show characteristic changes in flux, corresponding to a light curve similar to those in Fig. 2.35. The number density of MACHOs is proportional to the probability or abundance of lensing events, and the characteristic mass of the MACHOs is proportional to the square of the typical variation time scale t _E. All one has to do is measure the light curves of a sufficiently large number of background sources and extract all lens events from those light curves to obtain information on the population of potential MACHOs in the halo. A given halo model predicts the spatial density distribution and the distribution of velocities of the MACHOs and can therefore be compared to the observations in a statistical way. However, one faces the problem that the abundance of such lensing events is very small.

Probability of a lensing event. In practice, a system of a foreground lens and a background source is considered a lensing event if p ≤ 1, or β _min ≤ θ _E, and hence $\mu _{\mathrm{max}} \geq 3/\sqrt{5} \approx 1.34$ , i.e., if the relative trajectory of the source passes within the Einstein circle of the lens.

If the dark halo of the Milky Way consisted solely of MACHOs, the probability that a very distant source is lensed (in the sense of $\vert {\boldsymbol \beta }\vert \leq \theta _{\mathrm{E}}$ ) would be ∼ 10⁻⁷, where the exact value depends on the direction to the source. At any one time, one of ∼ 10⁷ distant sources would be located within the Einstein radius of a MACHO in our halo. The immediate consequence of this is that the light curves of millions of sources have to be monitored to detect this effect. Furthermore, these sources have to be located within a relatively small region on the sphere to keep the total solid angle that has to be photometrically monitored relatively small. This condition is needed to limit the required observing time, so that many such sources should be present within the field-of-view of the camera used. The stars of the Magellanic Clouds are well suited for such an experiment: they are close together on the sphere, but can still be resolved into individual stars.

Problems, and their solution. From this observational strategy, a large number of problems arise immediately; they were discussed in Paczyński’s original paper. First, the photometry of so many sources over many epochs produces a huge amount of data that need to be handled; they have to be stored and reduced. Second, one has the problem of ‘crowding’: the stars in the Magellanic Clouds are densely packed on the sky, which renders the photometry of individual stars difficult. Third, stars also show intrinsic variability—about 1 % of all stars are variable. This intrinsic variability has to be distinguished from that due to the lens effect. Due to the small probability of the latter, selecting the lensing events is comparable to searching for a needle in a haystack. Finally, it should be mentioned that one has to ensure that the experiment is indeed sensitive enough to detect lensing events. A ‘calibration experiment’ would therefore be desirable.

Faced with these problems, it seemed daring to seriously think about the realization of such an observing program. However, a fortunate event helped, in the magnificent time of the easing of tension between the US and the Soviet Union, and their respective allies, at the end of the 1980s. Physicists and astrophysicists, that had been partly occupied with issues concerning national security, then saw an opportunity to meet new challenges. In addition, scientists in national laboratories had much better access to sufficient computing power and storage capacity than those in other research institutes, attenuating some of the aforementioned problems. While the expected data volume was still a major problem in 1986, it could be handled a few years later. Also, wide-field cameras were constructed, with which large areas of the sky could be observed simultaneously. Software was developed specialized to the photometry of objects in crowded fields, so that light curves could be measured even if individual stars in the image were no longer cleanly separated.

To distinguish between lensing events and intrinsic variability of stars, we note that the microlensing light curves have a characteristic shape that is described by only four parameters. The light curves should be symmetric and achromatic because gravitational light deflection is independent of the frequency of the radiation. Furthermore, due to the small lensing probability, any source should experience at most one microlensing event and show a constant flux before and after, whereas intrinsic variations of stars are often periodic and in nearly all cases chromatic.

And finally a control experiment could be performed: the lensing probability in the direction of the Galactic bulge is known, or at least, we can obtain a lower limit for it from the observed density of stars in the disk. If a microlens experiment is carried out in the direction of the Galactic bulge, we have to find lensing events if the experiment is sufficiently sensitive.

2.5.3 Surveys and results

In the early 1990s, two collaborations (MACHO and EROS) began the search for microlensing events towards the Magellanic Clouds. Another group (OGLE) started searching in an area of the Galactic bulge. Fields in the respective survey regions were observed regularly, typically once every night if weather conditions permitted. From the photometry of the stars in the fields, light curves for many millions of stars were generated and then checked for microlensing events.

First detections. In 1993, all three groups reported their first results. The MACHO collaboration found one event in the Large Magellanic Cloud (LMC), the EROS group two events, and the OGLE group observed one event in the Galactic bulge. The light curve of the first MACHO event is plotted in Fig. 2.36. It was observed in two different filters, and the fit to the data, which corresponds to a standard light curve (2.93), is the same for both filters, proving that the event is achromatic. Together with the quality of the fit to the data, this is very strong evidence for the microlensing nature of the event.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig36_HTML.jpg

Fig. 2.36

Light curve of the first observed microlensing event in the LMC, in two broad-band filters. The solid curve is the best-fitting microlensing light curve as described by (2.93), with μ _max = 6. 86. The ratio of the magnifications in both filters is displayed at the bottom, and it is compatible with 1. Some of the data points deviate significantly from the curve; this means that either the errors in the measurements were underestimated, or this event is more complicated than one described by a point-mass lens—see Sect. 2.5.4. Source: C. Alcock et al. 1993, Possible gravitational microlensing of a star in the Large Magellanic Cloud, Nature 365, 621

Fig. 2.37

In this 8^∘× 8^∘ image of the LMC, 30 fields are marked in red which the MACHO group has searched for microlensing events during the ∼ 5. 5 yr of their experiment; images were taken in two filters to test for achromaticity. The positions of 17 microlensing events are marked by yellow circles; these have been subject to statistical analysis. Source: C. Alcock et al. 2000, The MACHO Project: Microlensing Results from 5.7 Years of Large Magellanic Cloud Observations, ApJ 542, 281, p. 284, Fig. 1. ©AAS. Reproduced with permission

Statistical results. After 1993, all three aforementioned teams proceeded with their observations and analysis (Fig. 2.37), and more groups have begun the search for microlensing events, choosing various lines of sight. The most important results from these experiments can be summarized as follows:

About 20 events have been found in the direction of the Magellanic Clouds, and some ten thousand in the direction of the bulge. The statistical analysis of the data revealed the lensing probability towards the bulge to be higher than originally expected. This can be explained by the fact that our Galaxy features a bar (see Chap. 3). This bar was also observed in IR maps such as those made by the COBE satellite. The events in the direction of the bulge are dominated by lenses that are part of the bulge themselves, and their column density is increased by the bar-like shape of the bulge. On the other hand, the lensing probability in the direction of the Magellanic Clouds is much smaller than expected for the case where the dark halo consists solely of MACHOs. Based on the analysis of the MACHO collaboration, the observed statistics of lensing events towards the Magellanic Clouds is best explained if about 20 % of the halo mass consists of MACHOs, with a characteristic mass of about M ∼ 0. 5M _⊙ (see Fig. 2.38).

Fig. 2.38

Probability contours for a specific halo model as a function of the characteristic MACHO mass M (here denoted by m) and the mass fraction f of MACHOs in the halo. The halo of the LMC was either taken into account as an additional source for microlenses (lmc halo) or not (no lmc halo), and two different selection criteria (A, B) for the statistically complete microlensing sample were employed. In all cases, M ∼ 0. 5M _⊙ and f ∼ 0. 2 are the best-fit values. Source: C. Alcock et al. 2000, The MACHO Project: Microlensing Results from 5.7 Years of Large Magellanic Cloud Observations, ApJ 542, 281, p. 304, Fig. 12. ©AAS. Reproduced with permission

Interpretation and discussion. This latter result is not easy to interpret and came as a real surprise. If a result compatible with ∼ 100 % had been found, it would have been obvious to conclude that the dark matter in our Milky Way consists of compact objects. Otherwise, if very few lensing events had been found, it would have been clear that MACHOs do not contribute significantly to the dark matter. But a value of 20 % does not immediately allow any unambiguous interpretation. Taken at face value, the result from the MACHO group would imply that the total mass of MACHOs in the Milky Way halo is about the same as that in the stellar disk.

Furthermore, the estimated mass scale is hard to understand: what could be the nature of MACHOs with M = 0. 5M _⊙? Normal stars can be excluded, because they would be far too luminous to escape direct observations. White dwarfs are also unsuitable candidates, because to produce such a large number of white dwarfs as a final stage of stellar evolution, the total star formation in our Milky Way, integrated over its lifetime, needs to be significantly larger than normally assumed. In this case, many more massive stars would also have formed, which would then have released the metals they produced into the ISM, both by stellar winds and in supernova explosions. In such a scenario, the metal content of the ISM would therefore be distinctly higher than is actually observed. The only possibility of escaping this argument is with the hypothesis that the mass function of newly formed stars (the initial mass function, IMF) was different in the early phase of the Milky Way compared to that observed today. The IMF that needs to be assumed in this case is such that for each star of intermediate mass which evolves into a white dwarf, far fewer high-mass stars, mainly responsible for the metal enrichment of the ISM, must have formed in the past compared to today. However, we lack a plausible physical model for such a scenario, and it is in conflict with the star-formation history that we observe in the high-redshift Universe (see Chap. 9).

Neutron stars can be excluded as well, because they are too massive (typically > 1M _⊙); in addition, they are formed in supernova explosions, implying that the aforementioned metallicity problem would be even greater for neutron stars. Would stellar-mass black holes be an alternative? The answer to this question depends on how they are formed. They could not originate in SN explosions, again because of the metallicity problem. If they had formed in a very early phase of the Universe (they are then called primordial black holes), this would be an imaginable, though perhaps quite exotic, alternative.

However, we have strong indications that the interpretation of the MACHO results is not as straightforward as described above. Some doubts have been raised as to whether all events reported as being due to microlensing are in fact caused by this effect. In fact, one of the microlensing source stars identified by the MACHO group showed another bump 7 years after the first event. Given the extremely small likelihood of two microlensing events happening to a single source this is almost certainly a star with unusual variability. There are good arguments to attribute two events to stars in the thick disk.

Fig. 2.39

From observations by the EROS collaboration, a large mass range for MACHO candidates can be excluded. The maximum allowed fraction of the halo mass contained in MACHOs is plotted as a function of the MACHO mass M, as an upper limit with 95 % confidence. A standard model for the mass distribution in the Galactic halo was assumed which describes the rotation curve of the Milky Way quite well. The various curves show different phases of the EROS experiment. They are plotted separately for observations in the directions of the LMC and the SMC. The experiment EROS 1 searched for microlensing events on short time-scales but did not find any; this yields the upper limits at small masses. Upper limits at larger masses were obtained by the EROS 2 experiment. The thick solid curve represents the upper limit derived from combining the individual experiments. If not a single MACHO event had been found the upper limit would have been described by the dotted line. Source: C. Afonso et al. 2003, Limits on Galactic dark matter with 5 years of EROS SMC data, A&A 400, 951, p. 955, Fig. 3. ©ESO. Reproduced with permission

As argued previously, by means of t _E we only measure a combination of lens mass, transverse velocity, and distance. The result given in Fig. 2.38 is therefore based on the statistical analysis of the lensing events in the framework of a halo model that describes the shape and the radial density profile of the halo. However, microlensing events have been observed for which more than just t _E can be determined—e.g., events in which the lens is a binary star, or those for which t _E is larger than a few months. In this case, the orbit of the Earth around the Sun, which is not a linear motion, has a noticeable effect, causing deviations from the standard light curve. Such parallax events have indeed been observed.¹⁶ Three events are known in the direction of the Magellanic Clouds in which more than just t _E could be measured. In all three cases the lenses are most likely located in the Magellanic Clouds themselves (an effect called self-lensing) and not in the halo of the Milky Way. If for those three cases, where the degeneracy between lens mass, distance, and transverse velocity can be broken, the respective lenses are not MACHOs in the Galactic halo, we might then suspect that in most of the other microlensing events the lens is not a MACHO either. Therefore, it is currently unclear how to interpret the results of the MACHO survey. In particular, it is unclear to what extent self-lensing contributes to the results. Furthermore, the quantitative results depend on the halo model.

The EROS collaboration used an observation strategy which was sightly different from that of the MACHO group, by observing a number of fields in very short time intervals. Since the duration of a lensing event depends on the mass of the lens as Δ t ∝ M ^1∕2—see (2.91)—they were also able to probe very small MACHO masses. The absence of lensing events of very short duration then allowed them to derive limits for the mass fraction of such low-mass MACHOs, as is shown in Fig. 2.39. In particular, neither the EROS nor the OGLE group could reproduce the relatively large event rate found by the MACHO group; indeed, the EROS and OGLE results do not require any unknown component of compact objects in our Milky Way, and OGLE derived an upper bound of ∼ 2 % of the dark matter in our Milky Way which could be in the form of compact objects.

We have to emphasize that the microlensing surveys have been enormously successful experiments because they accomplished exactly what was expected at the beginning of the observations. They measured the lensing probability in the direction of the Magellanic Clouds and the Galactic bulge, excluded the possibility that a major fraction of the dark matter is in compact objects, and revealed the structure of the Galactic bulge.

The microlensing surveys did not constrain the density of compact objects with masses ≳ 10M _⊙, since the variability time-scale from such high-mass lenses becomes comparable to the survey duration. Whereas such high-mass MACHOs are physically even less plausible than ∼ 0. 5 M _⊙ candidates, it still would be good to be able to rule them out. This can be done by studying wide binary systems in the stellar halo. If the dark matter in our Galaxy would be present in form of high-mass MACHOs, these would affect the binary population, in particular by disrupting wide binaries. From considering the separation distribution of halo binaries, it can be excluded that high-mass compact objects constitute the dark matter in the Galactic halo.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig40_HTML.jpg

Fig. 2.40

If a binary star acts as a lens, significantly more complicated light curves can be generated. In the left-hand panel tracks are plotted for five different relative motions of a background source; the dashed curve is the so-called critical curve, formally defined by $\det (\partial {\boldsymbol \beta }/\partial {\boldsymbol \theta }) = 0$ , and the solid line is the corresponding image of the critical curve in the source plane, called a caustic. Light curves corresponding to these five tracks are plotted in the right-hand panel. If the source crosses the caustic, the magnification μ becomes very large—formally infinite if the source was point-like. Since it has a finite extent, μ has to be finite as well; from the maximum μ during caustic crossing, the radius of the source can be determined, and sometimes even the variation of the surface brightness across the stellar disk, an effect known as limb darkening. Source: B. Paczyński 1996, Gravitational Microlensing in the Local Group ARA&A 34, 419, p. 435, 434. Reprinted, with permission, from the Annual Review of Astronomy & Astrophysics, Volume 34 ©1996 by Annual Reviews www.annualreviews.org

2.5.4 Variations and extensions

Besides the search for MACHOs, microlensing surveys have yielded other important results and will continue to do so in the future. For instance, the distribution of stars in the Galaxy can be measured by analyzing the lensing probability as a function of direction. A huge number of variable stars have been newly discovered and accurately monitored; the extensive and publicly accessible databases of the surveys form an invaluable resource for stellar astrophysics. Proper motions of several million stars have been determined, based on ∼ 20 yr of microlensing surveys. Furthermore, globular clusters in the LMC have been identified from these photometric observations.

For some lensing events, the radius and the surface structure of distant stars can be measured with very high precision. This is possible because the magnification μ depends on the position of the source. Situations can occur, for example where a binary star acts as a lens (see Fig. 2.40), in which the dependence of the magnification on the position in the source plane is very sensitive. Since the source—the star—is in motion relative to the line-of-sight between Earth and the lens, its different regions are subject to different magnification, depending on the time-dependent source position. A detailed analysis of the light curve of such events then enables us to reconstruct the light distribution on the surface of the star. The light curve of one such event is shown in Fig. 2.41. For these lensing events the source can no longer be assumed to be a point source. Rather, the details of the light curve are determined by its light distribution. Therefore, another length-scale appears in the system, the radius of the star. This length-scale shows up in the corresponding microlensing light curve, as can be seen in Fig. 2.41, by the time-scale which characterizes the width of the peaks in the light curve—it is directly related to the ratio of the stellar radius and the transverse velocity of the lens. With this new scale, the degeneracy between M, v, and D _d is partially broken, so that these special events provide more information than the ‘classical’ ones.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig41_HTML.jpg

Fig. 2.41

Light curve of an event in which the lens was a binary star. Note the qualitative similarity of this light curve with the second one from the top in Fig. 2.40. The MACHO group discovered this ‘binary event’. Members of the PLANET collaboration obtained this data using four different telescopes (in Chile, Tasmania, and South Africa). The second caustic crossing is highly resolved (displayed in the small diagram) and allows us to draw conclusions about the size and the brightness distribution of the source star. The two curves show the fits of a binary lens to the data. Source: M.D. Albrow et al. 1999, The Relative Lens-Source Proper Motion in MACHO 98-SMC-1, ApJ 512, 672, p. 674, Fig. 2. ©AAS. Reproduced with permission

In fact, the light curve in Fig. 2.36 is probably not caused by a single lens star, but instead by additional slight disturbances from a companion star. This would explain the deviation of the observed light curve from a simple model light curve. However, the sampling in time of this particular light curve is not sufficient to determine the parameters of the binary system.

By now, detailed light curves with very good time coverage have been measured, which was made possible with an alarm system. The data from those groups searching for microlensing events are analyzed immediately after observations, and potential candidates for interesting events are published on the Internet. Other groups (such as the PLANET collaboration, for example) then follow-up these systems with very good time coverage by using several telescopes spread over a large range in geographical longitude. This makes around-the-clock observations of the events possible. Using this method, light curves of extremely high quality have been measured, and events in which the lens is a binary with a very large mass ratio have been detected—so large that the lighter of the two masses is not a star, but a planet. Indeed, more than a dozen extrasolar planets have been found by microlensing surveys. Whereas this number at first sight is not so impressive, given that many more extrasolar planets were discovered by other methods, the selection function in microlensing surveys is quite different. In contrast to the radial velocity method (where the periodic change of the radial velocity of the parent star, caused by its motion around the center of mass of the star-planet system, is measured), microlensing has detected lower-mass planets and planets at larger separation from the host star.

2.6 The Galactic center

The Galactic center (GC, see Fig. 2.42) is not observable at optical wavelengths, because the extinction in the V band is ∼ 28 mag. Our information about the GC has been obtained from radio-, IR-, and X-ray radiation, although even in the K-band, the extinction is still ∼ 3 mag. Since the GC is nearby, and thus serves as a prototype of the central regions of galaxies, its observation is of great interest for our understanding of the processes taking place in the centers of galaxies.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig42_HTML.jpg

Fig. 2.42

Optical image in the direction of the Galactic center. The size of the image is ∼ 10^∘× 15^∘. Marked are some Messier objects: gas nebulae such as M8, M16, M17, M20; open star clusters such as M6, M7, M18, M21, M23, M24, and M25; globular clusters such as M9, M22, M28, M54, M69, and M70. Also marked is the Galactic center, as well as the Galactic plane, which is indicated by a line. Baade’s Window can be easily recognized, a direction in which the extinction is significantly lower than in nearby directions, so that a clear increase in stellar density is visible there. This is the reason why the microlensing observations towards the Galactic center were preferably done in Baade’s Window. Credit: W. Keel (U. Alabama, Tuscaloosa), Cerro Tololo, Chile

2.6.1 Where is the Galactic center?

The question of where the center of our Milky Way is located is by no means trivial, because the term ‘center’ is in fact not well-defined. Is it the center of mass of the Galaxy, or the point around which the stars and the gas are orbiting? And how could we pinpoint this ‘center’ accurately? Fortunately, the center can nevertheless be localized because, as we will see below, a distinct source exists that is readily identified as the Galactic center.

Fig. 2.43

Left: A VLA wide-field image of the region around the Galactic center, with a large number of sources identified. Upper right: a 20 cm continuum VLA image of Sgr A East. Center right: Sgr A West, as seen in a 6-cm continuum VLA image, where the red dot marks Sgr A^∗. Lower right: the circumnuclear ring in HCN line emission. Source: Left: N.E. Kassim, from T.N. LaRosa et al. 2000, A Wide-Field 90 Centimeter VLA Image of the Galactic Center Region, AJ 119, 207, P. 209, Fig. 1. ©AAS. Reproduced with permission. Credit: Produced by the U.S. Naval Research Laboratory by Dr. N.E. Kassim and collaborators from data obtained with the National Radio Astronomy’s Very Large Array Telescope, a facility of the National Science Foundation operated under the cooperative agreement with associated Universities, Inc. Basic research in radio astronomy is supported by the U.S. Office of Naval Research. Upper right: from R.L. Plante et al. 1995, The magnetic fields in the galactic center: Detection of H1 Zeeman splitting, ApJ 445, L113, Fig. 1. ©AAS. Reproduced with permission. Center right: Image courtesy of NRAO/AUI, National Radio Astronomy Observatory. Lower right: Image courtesy of Leo Blitz and Hat Creek Observatory

Radio observations in the direction of the GC show a relatively complex structure, as is displayed in Fig. 2.43. A central disk of Hi gas exists at radii from several 100 pc up to about 1 kpc. Its rotational velocity yields an estimate of the enclosed mass M(R) for R ≳ 100 pc. Furthermore, radio filaments are observed which extend perpendicularly to the Galactic plane, and a large number of supernova remnants are seen. Within about 2 kpc from the center, roughly 3 × 10⁷ M _⊙ of atomic hydrogen is found. Optical images show regions close to the GC towards which the extinction is significantly lower. The best known of these is Baade’s Window —most of the microlensing surveys towards the bulge are conducted in this region. It is the brightest region in Fig. 2.42, not because the stellar density is highest there, but the obscuration is smallest. In addition, a fairly large number of globular clusters and gas nebulae are observed towards the central region. X-ray images (Fig. 2.44) show numerous X-ray binaries, as well as diffuse emission by hot gas.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig44_HTML.jpg

Fig. 2.44

A composite image of the Galactic center: X-ray emission as observed by Chandra is shown in blue, mid-infrared emission (Spitzer) shown in red, and near-IR radiation (HST) in yellow-brown. The long side of the image is 32. ^′ 5, corresponding to ∼ 75 pc at the distance of the Galactic center. The Galactic center, in which a supermassive black hole is suspected to reside, is the bright white region to the right of the center of this image. The X-ray image contains hundreds of white dwarfs, neutron stars, and black holes that radiate in the X-ray regime due to accretion phenomena (accreting X-ray binaries). The diffuse X-ray emission originates in diffuse hot gas with a temperature of about T ∼ 10⁷ K. Credit: NASA, ESA, CXC, SSC, and STScI

The innermost 8 pc contain the radio source Sgr A (Sagittarius A), which itself consists of different components:

A circumnuclear molecular ring, shaped like a torus, which extends between radii of 2 pc ≲ R ≲ 8 pc and is inclined by about 20^∘ relative to the Galactic disk. The rotational velocity of this ring is about ∼ 110 km∕s, nearly independent of R. This ring has a sharp inner boundary; this cannot be the result of an equilibrium flow, because internal turbulent motions would quickly (on a time scale of ∼ 10⁵ yr) blur this boundary. Probably, it is evidence of an energetic event that occurred in the Galactic center within the past ∼ 10⁵ yr. This interpretation is also supported by other observations, e.g., by a clumpiness in density and temperature.
Sgr A East, a non-thermal (synchrotron) source of shell-like structure. Presumably this is a supernova remnant (SNR), with an age between 100 and 5000 years.
Sgr A West is located about 1. ^′ 5 away from Sgr A East. It is a thermal source, an unusual Hii region with a spiral-like structure.
Sgr A^∗ is a compact radio source close to the center of Sgr A West. Recent observations with mm-VLBI show that its extent is smaller than about 1 AU. The radio luminosity is L _rad ∼ 2 × 10³⁴ erg∕s. Except for the emission in the mm and cm domain, Sgr A^∗ is a weak source. Since other galaxies often have a compact radio source in their center, Sgr A^∗ is an excellent candidate for being the center of our Milky Way.

Through observations of stars which contain a radio maser¹⁷ source, the astrometry of the GC in the radio domain was matched to that in the IR, i.e., the position of Sgr A^∗ is also known in the IR.¹⁸ The uncertainty in the relative positions between radio and IR observations is only ∼ 30 mas—at a presumed distance of the GC of 8 kpc, 1 arcsec corresponds to 0.0388 pc, or about 8000 AU.

2.6.2 The central star cluster

Density distribution. Observations in the K-band (λ ∼ 2μm) show a compact star cluster that is centered on Sgr A^∗. Its density behaves like ∝ r ^−1. 8 within the distance range 0. 1 pc ≲ r ≲ 1 pc. The number density of stars in its inner region is so large that close stellar encounters may be common. It can be estimated that a star has a close encounter about every ∼ 10⁶ yr. Thus, it is expected that the distribution of the stars is ‘thermalized’, which means that the local velocity distribution of the stars is the same everywhere, i.e., it is close to a Maxwellian distribution with a constant velocity dispersion. For such an isothermal distribution we expect a density profile n ∝ r ⁻², which is in good agreement with the observation. Most of the stars in the nuclear star cluster have an age ≳ 1 Gyr; they are late-type giant stars.

In addition, young O and B stars are found in the central parsec. From their spectroscopic observations, it was inferred that almost all of these hot, young stars reside in one of two rotating thick disks. These disks are strongly inclined to the Galactic plane, one rotates ‘clockwise’ around the GC, the other ‘counterclockwise’. These two disks have a clearly defined inner edge at about 1″, corresponding to 0. 04 pc, and a surface mass density ∝ r ⁻². The age of these early-type stars is 6 ± 2 Myr, i.e., of the same order as the time between two strong encounters.

Another observational result yields a striking and interesting discrepancy with respect to the idea of an isothermal distribution. Instead of the expected constant dispersion σ of the radial velocities of the stars, a strong radial dependence is observed: σ increases towards smaller r. For example, one finds σ ∼ 55 km∕s at r = 5 pc, but σ ∼ 180 km∕s at r = 0. 15 pc. This discrepancy indicates that the gravitational potential in which the stars are moving is generated not only by themselves. According to the virial theorem, the strong increase of σ for small r implies the presence of a central mass concentration in the star cluster.

The origin of very massive stars near the GC. One of the unsolved problems is the presence of these massive stars close to the Galactic center. One finds that most of the innermost stars are main-sequence B-stars. Their small lifetime of ∼ 10⁸ yr probably implies that these stars were born close to the Galactic center. This, however, is very difficult to understand. Both the strong tidal gravitational field of the central black hole (see below) and the presumably strong magnetic field in this region will prevent the ‘standard’ star-formation picture of a collapsing molecular cloud: the former effect tends to disrupt such a cloud while the latter stabilizes it against gravitational contraction. In order to form the early-type stars found in the inner parsec of the Galaxy, the gas clouds need to be considerably denser than currently observed, but may have been at some earlier time during a phase of strong gas infall. Several other solutions to this problem have been suggested. Perhaps the most plausible is a scenario in which the stars are born at larger distances from the Galactic center and then brought there by dynamical processes, involving strong gravitational scattering events. If a stellar binary has an orbit which brings it close to the central region, the strong tidal gravitational field can disrupt the binary, with one of its star being brought into a gravitationally bound orbit around the black hole, and the other being expelled from the central region.

Proper motions. Since the middle of the 1990s, proper motions of stars in this star cluster have also been measured, using the methods of speckle interferometry and adaptive optics. These produce images at diffraction-limited angular resolution, about ∼ 0. ^′
′ 15 in the K-band at the ESO/NTT (3.5 m) and about ∼ 0. ^′
′ 05 at 10 m-class telescopes. Proper motions are currently known for about 6000 stars within ∼ 1 pc of Sgr A^∗, of which some 700 additionally have radial velocity measurements, so that their three-dimensional velocity vector is known. The radial and tangential velocity dispersions resulting from these measurements are in good mutual agreement. Thus, it can be concluded that a basically isotropic distribution of the stellar orbits exists, simplifying the study of the dynamics of this stellar cluster.

2.6.3 A black hole in the center of the Milky Way

The S-star cluster. Whereas the distribution of young A-stars in the nuclear disks shows a sharp cut-off at around 1″, there is a distribution of stars within ∼ 1″ of Sgr A^∗ which is composed mainly of B-stars; these are known as the S-star cluster. Some stars of this cluster have a proper motion well in excess of 1000 km∕s, up to ∼ 10000 km∕s. Combining the velocity dispersions in radial and tangential directions reveals them to be increasing according to the Kepler law for the presence of a point mass, $\sigma \propto r^{-1/2}$ down to r ∼ 0. 01 pc.

Fig. 2.45

The left figure shows the orbits of about two dozen stars in the central arcsecond around Sgr A^∗, as determined from their measured proper motions and radial velocity. For one of the stars, denoted by S2, a full orbit has been observed, as shown in the upper right panel. The data shown here were obtained between 1992 and 2008, using data taken with the NTT and the VLT (blue points) and the Keck telescopes (red points). The orbital time is 15. 8 yr, and the orbit has a strong eccentricity. The lower right panel shows the radial velocity measurements of S2. In both of the right panels, the best fitting model for the orbital motion is plotted as a curve. Source: Left: S. Gillessen et al. 2009, Monitoring Stellar Orbits Around the Massive Black Hole in the Galactic Center, ApJ 692, 1075, p. 1096, Fig. 16. ©AAS. Reproduced with permission. Right: S. Gillessen et al. 2009, The Orbit of the Star S2 Around SGR A ^∗ from Very Large Telescope and Keck Data, ApJ 707, L114, p. L115, L116, Figs. 2 & 3. ©AAS. Reproduced with permission

Fig. 2.46

Determination of the mass M(r) within a radius r from Sgr A^∗, as measured by the radial velocities and proper motions of stars in the central cluster. Mass estimates obtained from individual stars (S14, S2, S12) are given by the points with error bars for small r. The other data points were derived from the kinematic analysis of the observed proper motions of the stars, where different methods have been applied. As can be seen, these methods produce results that are mutually compatible, so that the shape of the mass profile plotted here can be regarded to be robust, whereas the normalization depends on R ₀ which was assumed to be 8 kpc for this figure. The solid curve is the best-fit model, representing a point mass of 2. 9 × 10⁶ M _⊙ plus a star cluster with a central density of $3.6 \times 10^{6}M_{\odot }/\mathrm{pc}^{3}$ (the mass profile of this star cluster is indicated by the dash-dotted curve). The dashed curve shows the mass profile of a hypothetical cluster with a very steep profile, n ∝ r ⁻⁵, and a central density of $2.2 \times 10^{17}M_{\odot }\,\mathrm{pc}^{-3}$ . Source: R. Schödel et al. 2003, Stellar Dynamics in the Central Arcsecond of Our Galaxy, ApJ 596, 1015, p. 1027, Fig. 11. ©AAS. Reproduced with permission

By now, the acceleration of some stars in the star cluster has also been measured, i.e., the change of proper motion with time, which is a direct measure of the gravitational force. From these measurements Sgr A^∗ indeed emerges as the focus of the orbits and thus as the center of mass. For ∼ 25 members of the S-star cluster, the information from proper motion and radial velocity measurements allowed the reconstruction of orbits; these are shown in the left-hand panel of Fig. 2.45. For one of these stars, S2, observations between 1992 and 2008 have covered a full orbit around Sgr A^∗, with an orbital period of 15. 8 yr, as shown in the right panels of Fig. 2.45. Its velocity exceeded 5000 km∕s when it was closest to Sgr A^∗. The minimum separation of this star from Sgr A^∗ then was only 6 × 10⁻⁴ pc, or about 100 AU. In 2012, a new S-star with a period of only 11. 5 yr wasdiscovered.

From the observed kinematics of the stars, the enclosed mass M(r) can be calculated, see Fig. 2.46. The corresponding analysis yields that M(r) is basically constant over the range 0. 01 pc ≲ r ≲ 0. 5 pc. This exciting result clearly indicates the presence of a point mass. The precise value of this mass is a bit uncertain, mainly due to the uncertainty in the distance of the Galactic center from us. A characteristic value obtained from recent analysis yields a distance to the Galactic center of R ₀ ≈ 8. 3 kpc, and a blackhole mass of

$\displaystyle\begin{array}{rcl} \fbox{$M = (4.3 \pm 0.4) \times 10^{6}M_{ \odot }$}\;,& &{}\end{array}$

(2.94)

which is slightly larger than the estimate based on the data shown in Fig. 2.46. For radii above ∼ 1 pc, the mass of the star cluster dominates; it nearly follows an isothermal density distribution with a core radius of ∼ 0. 34 pc and a central density of $3.6 \times 10^{6}M_{\odot }/\mathrm{pc}^{3}$ . This result is also compatible with the kinematics of the gas in the center of the Galaxy. However, stars are much better kinematic indicators because gas can be affected by magnetic fields, viscosity, and various other processes besides gravity.

The kinematics of stars in the central star cluster of the Galaxy shows that our Milky Way contains a mass concentration in which ∼ 4 × 10⁶ M _⊙ are concentrated within a region smaller than 0.01 pc. This is almost certainly a black hole in the center of our Galaxy, at the position of the compact radio source Sgr A^∗.

Why a black hole? We have interpreted the central mass concentration as a black hole; this requires some further explanation:

The energy for the central activity in quasars, radio galaxies, and other AGNs is produced by accretion of gas onto a supermassive black hole (SMBH); we will discuss this in more detail in Sect. 5.3. Thus we know that at least a sub-class of galaxies contains a central SMBH. Furthermore, we will see in Sect. 3.8 that many ‘normal’ galaxies, especially ellipticals, harbor a black hole in their center. The presence of a black hole in the center of our own Galaxy would therefore not be something unusual.
To bring the radial mass profile M(r), as inferred from the stellar kinematics, into accordance with an extended mass distribution, its density distribution must be very strongly concentrated, with a density profile steeper than ∝ r ⁻⁴; otherwise the mass profile M(r) would not be as flat as observed and shown in Fig. 2.46. Hence, this hypothetical mass distribution must be vastly different from the expected isothermal distribution which has a mass profile ∝ r ⁻², as discussed in Sect. 2.6.2. However, observations of the stellar distribution provide no indication of an inwardly increasing density of the star cluster with such a steep profile.
Even if such an ultra-dense star cluster (with a central density of $\gtrsim 4 \times 10^{12}M_{\odot }/\mathrm{pc}^{3}$ ) was present it could not be stable, but instead would dissolve within ∼ 10⁷ yr through frequent stellar collisions.
Sgr A^∗ itself has a proper motion of less than 20 km/s. It is therefore the dynamical center of the Milky Way. Due to the large velocities of its surrounding stars, one would derive a mass of $M \gg 10^{3}M_{\odot }$ for the radio source, assuming equipartition of energy (see also Sect. 2.6.4). Together with the tight upper bounds for its extent, a lower limit for the density of $10^{18}M_{\odot }/\mathrm{pc}^{3}$ can then beobtained.

We have to emphasize at this point that the gravitational effect of the black hole on the motion of stars and gas is constrained to the innermost region of the Milky Way. As one can see from Fig. 2.46, the gravitational field of the SMBH dominates the rotation curve of the Galaxy only for R ≲ 2 pc—this is the very reason why the detection of the SMBH is so difficult. At larger radii, the presence of the SMBH is of no relevance for the rotation curve of the Milky Way.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig47_HTML.jpg

Fig. 2.47

The position of Sgr A^∗ at different epochs, relative to the position in 1996. To a very good approximation the motion is linear, as indicated by the dashed best-fit straight line. In comparison, the solid line shows the orientation of the Galactic plane. Source: M. Reid & A. Brunthaler 2004, The Proper Motion of Sagittarius A ^∗ . II. The Mass of Sagittarius A ^∗, ApJ 616, 872, p. 875, Fig. 1. ©AAS. Reproduced with permission

2.6.4 The proper motion of Sgr A^∗

From a series of VLBI observations of the position of Sgr A^∗, covering 8 years, the proper motion of this compact radio source was measured with very high precision. To do this, the position of Sgr A^∗ was determined relative to two compact extragalactic radio sources. Due to their large distances these are not expected to show any proper motion, and the VLBI measurements show that their separation vector is indeed constant over time. The position of Sgr A^∗ over the observing period is plotted in Fig. 2.47.

From the plot, we can conclude that the observed proper motion of Sgr A^∗ is essentially parallel to the Galactic plane. The proper motion perpendicular to the Galactic plane is about 0. 2 mas∕yr, compared to the proper motion in the Galactic plane of 6. 4 mas∕yr. If R ₀ = (8. 0 ± 0. 5) kpc is assumed for the distance to the GC, this proper motion translates into an orbital velocity of (241 ± 15) km∕s, where the uncertainty is dominated by the exact value of R ₀ (the error in the measurement alone would yield an uncertainty of only 1 km∕s). This proper motion is easily explained by the Solar orbital motion around the GC, i.e., this measurement contains no hint of a non-zero velocity of the radio source Sgr A^∗ itself. In fact, the small deviation of the proper motion from the orientation of the Galactic plane can be explained by the peculiar velocity of the Sun relative to the LSR (see Sect. 2.4.1). If this is taken into account, a velocity perpendicular to the Galactic disk of $v_{\perp } = (-0.4 \pm 0.9)\,\mathrm{km/s}$ is obtained for Sgr A^∗. The component of the orbital velocity within the disk has a much larger uncertainty because we know neither R ₀ nor the rotational velocity V ₀ of the LSR very precisely. The small upper limit for v _⊥ suggests, however, that the motion in the disk should also be very small. Under the (therefore plausible) assumption that Sgr A^∗ has no peculiar velocity, the ratio $R_{0}/V _{0}$ can be determined from these measurements with an as yet unmatched precision.

What also makes this observation so impressive is that from it we can directly derive a lower limit for the mass of Sgr A^∗. Since this radio source is surrounded by ∼ 10⁶ stars within a sphere of radius ∼ 1 pc, the net acceleration towards the center is not vanishing, even in the case of a statistically isotropic distribution of stars. Rather, due to the discrete nature of the mass distribution, a stochastic force exists that changes with time because of the orbital motion of the stars. The radio source is accelerated by this force, causing a motion of Sgr A^∗ which becomes larger the smaller the mass of the source. The very strong limits to the velocity of Sgr A^∗ enable us to derive a lower limit for its mass of $0.4 \times 10^{6}M_{\odot }$ . This mass limit is significantly lower than the mass of the SMBH that was derived from the stellar orbits, but it is the mass of the radio source itself. Although we have excellent reasons to assume that Sgr A^∗ coincides with the SMBH, the upper limit on the peculiar velocity of Sgr A^∗ is the first proof for a large mass of the radio source itself.

2.6.5 Flares from the Galactic center

Observation of flares. In 2000, the X-ray satellite Chandra discovered a powerful X-ray flare from Sgr A^∗. This event lasted for about 3 h, and the X-ray flux increased by a factor of 40 during this period. XMM-Newton confirmed the existence of X-ray flares, recording one where the luminosity increased by a factor of ∼ 200. Most of the flares seen, however, have a much smaller peak amplitude, of a few to ten times the quiescent flux of the source, and the typical flare duration is ∼ 30 min. During the flares, variability of the X-flux on time-scales of several minutes is observed. Combining the flare duration with the short time-scale of variability of a few minutes indicates that the emission must originate from a very small source, not larger than ∼ 10¹³ cm in size.

Fig. 2.48

Variability of Sgr A^∗ is shown here in simultaneous observations at four different wavelengths, carried out in May 2009. The red bars in each panel are the error bars of the observed flux, from which the quiescent flux level was subtracted, with their central values connected with a thin line. The thick solid curve corresponds to a model for the flare emission across the wavebands, whereas the other three curves (dashed, blue and red) are individual components of this model. One sees that the first flare occurs at all wavelength, whereas the second, main flare, was not covered by the near-IR observations. Source: A. Eckart et al. 2012, Millimeter to X-ray flares from Sagittarius A ^∗, A&A 537, A52, Fig. 1. ©ESO. Reproduced with permission

Monitoring Sgr A^∗ at longer wavelengths, variability was found as well. Figure 2.48 shows the simultaneous lightcurves of Sgr A^∗ during one night in May 2009. The source flared in X-rays, with two flares close in time. These flares are also seen at the near-IR, sub-mm and mm wavelengths, nearly simultaneously. Flares are seen more frequently in the NIR than in X-rays, occurring several times per day, where X-ray flares occur about once per day. Simultaneous observations, such as those in Fig. 2.48, indicate that every X-ray flare is accompanied by a flare in the NIR; the converse is not true, however. It thus seems that the flares in the different wavelength regimes have a common origin. From a set of such simultaneous observing campaigns, it was found that there is a time lag between the variations at different wavelengths. Typically, NIR flares occur ∼ 2 h earlier than those seen at (sub-)mm wavelengths, and they are narrower, whereas the X-ray and NIR flares are essentially simultaneous.

There was some discussion about a possible quasi-periodicity of the NIR light curves, but the observational evidence for this is not unambiguous. Nevertheless, polarization observation of Sgr A^∗ may provide support for a model in which the variability is caused by a source moving around the central black hole. Anticipating our discussion about AGN in Chap. 5, the model assumes that there is a ‘hot spot’ on the surface of an accretion disk, whereby relativistic effects modulate the received flux from this source component as it orbits around the black hole.

X-ray echos. With a mass of $M_{\bullet } \approx 4 \times 10^{6}\,M_{\odot }$ , the central black hole in the Milky Way could in principle power a rather luminous active galactic nucleus, such as is observed in other active galaxies, e.g., Seyfert galaxies. This, however, is obviously not the case—the luminosity of Sgr A^∗ is many orders of magnitudes smaller than the nucleus in Seyfert galaxies with similar mass central black holes (see Chap. 5). The reason for the inactivity of our Galactic center is therefore not the black hole mass, but the absence of matter which is accreted onto it. The fact that the Galactic center region emits thermal radiation in the X-rays shows the presence of gas. But this gas cannot flow to the central black hole, presumably because of its high temperature and associated high pressure. This line of argument is supported by the fact that the central X-ray source is resolved, and hence much more extended than the Schwarzschild radius of the black hole, where the bulk of the energy generation by accretion takes place (see Sect. 5.3.2 for more details). However, the variability of Sgr A^∗ may be seen as an indication that the accretion rate can change in the course of time.

Maybe there have been times when the luminosity of Sgr A^∗ was considerably larger than it is currently. Indeed, there are some indications for this being the case. Photons emitted at earlier times than the ones we observe now from Sgr A^∗ may still reach us today, if they were scattered by electrons, or if these photons have exited gas that, as a consequence, emits radiation. In both cases, the total light-travel time from the source to us would be larger, since the geometric light path is longer. We may therefore see the evidence of past activity as a light echo of radiation, which reaches us from slightly different directions.

There is now strong evidence for such a light echo. Hard X-ray radiation can lead to the removal of a strongly bound electron in iron, which subsequently emits a fluorescence line at 6. 4 keV. The distribution of this iron line radiation in a region close to Sgr A^∗ is shown in Fig. 2.49. This region contains a large number of molecular clouds, i.e., high-density neutral gas. The images in Fig. 2.49 show the variation of this line flux over a time period of about 5 year. We see that the spatial distribution of this line flux changes over this time-scale, with the flux increasing to the left part of this region as time progresses. The apparent velocity, with which the peak of the line emission moves across the region, is considerably larger than the speed of light—it shows superluminal motion. This evidence has recently been further strengthened with Chandra observations of the same region showing variations on even shorter time-scales. This high velocity, however, is not necessarily a violation of Einstein’s Special Relativity. In fact, this phenomenon can be easily understood in the framework of a reflection model: Suppose there is a screen of scattering material between us and a source. The further away a point in the screen is from the line connecting us and the source, the larger is the geometrical path of a ray which propagates to this point in the screen, and is scattered there towards our direction. The scattered radiation from a flare in the source will thus appear at different points in the screen as time progresses, and the speed with which the point changes in the screen can exceed the speed of light, without violating relativity; this will be shown explicitly in Problem 2.6. The argument is the same, independent of whether the light is scattered, or if a fluorescence line is excited. In fact, the material responsible for the light echo does not need to be located between us and the source, it can also be located behind the source.

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig49_HTML.jpg

Fig. 2.49

The flux distribution of the 6. 4 keV iron line in the region of molecular clouds near the Galactic center, at four different epochs. These XMM observations show that the flux distribution is changing on time-scales of a few years. However, the size of the region is much larger than a few light years—see the scale bar in the lower right panel. Thus, it seems that the variations are propagating through this region with a velocity larger than the speed of light. The explanation for this phenomenon is the occurrence of a light echo. Sgr A^∗ is located in the direction indicated by the white arrow in the upper right panel, at a projected distance of about 40 light-years from the molecular cloud MC2. Source: G. Ponti et al. 2010, Discovery of a Superluminal Fe K Echo at the Galactic Center: The Glorious Past of Sgr A* Preserved by Molecular Clouds, ApJ 714, 732, p. 742, Fig. 10. ©AAS. Reproduced with permission

/epubstore/S/P-Schneider/Extragalactic-Astronomy-And-Cosmology/OEBPS/A129044_2_En_2_Fig50_HTML.jpg

Fig. 2.50

Gamma-ray map of the sky in the energy range between 1 and 10 GeV. The Fermi-bubbles show up above and below the Galactic center, extending up to ∼ 50^∘ from the disk. Credit: NASA/DOE/Fermi LAT/D. Finkbeiner et al.

In fact, this phenomenon has not only be seen in the region shown in Fig. 2.49. The massive molecular cloud Sgr B2 also shows the prominent fluorescence line of iron, as well as X-ray continuum emission. The line and continuum flux decreased by a factor ∼ 2 over a time-scale of ∼ 10 yr—whereas the extent of the molecular cloud is much larger than ten light-years. Furthermore, there is no strong X-ray source known close to Sgr B2 which would be able to power the fluorescence line.

These observations are compatible with a model in which Sgr A^∗ had a strong flare some 100 yr ago, and what we see are the light echos of this flare. The luminosity of the flare must have exceeded 2 × 10³⁹ erg∕s in the X-ray regime, and it must have faded rather quickly, in order to generate such short-term variations of the echo. The location of the flare must be located in a region close to Sgr A^∗, though one cannot conclude with certainty that Sgr A^∗ was the exact location—there are several compact stellar remnants in its immediate vicinity which may have caused such a flare. Nevertheless, the requested luminosity is higher than that one usually assigns to compact stellar-mass objects, and Sgr A^∗ as the putative source of the flare appears quite likely. Hence, the light echo phenomenon gives us an opportunity to look back in time.

The Fermi bubbles. Another potential hint for an increased nuclear activity of the Galactic center was found with the Fermi satellite. It discovered two large structures in gamma-rays above and below the Galactic center, extending up to a Galactic latitude of | b | ≲ 50^∘, i.e., a spatial scale of ∼ 8 kpc from the center of the Milky Way (see Fig. 2.50). Emission from these regions is seen in the energy range between 1 and 100 GeV, with a hard energy spectrum, much harder than the diffuse gamma-ray emission from the Milky Way. The two ‘Fermi bubbles’ are associated with an enhanced microwave emission, seen by the WMAP and Planck satellites (the so-called microwave ‘haze’), and appear to have well-defined edges, which are also seen in X-rays. Furthermore, almost spatially coincident giant radio lobes with strong linear polarization were detected.

The origin of the Fermi bubbles is currently strongly debated in the literature. One possibility is strongly enhanced activity of Sgr A^∗ in the past, that drove out a strong flow of energetic plasma—similar to AGNs—and whose remnant we still see. Alternatively, the Galactic center region is a site of active star formation, which may be the origin of a massive outflow of magnetized plasma.

2.6.6 Hypervelocity stars in the Galaxy

Discovery. In 2005, a Galactic star was discovered which travels with a velocity of at least 700 km/s relative to the Galactic rest frame. This B-star has a distance of 110 kpc from the Galactic center, and its actual space velocity depends on its transverse motion which has not yet been measured, due to the large distance of the object from us. However, since the distance of the star is far larger than the separation between the Sun and the Galactic center, so that the directions Galactic center–star and Sun–star are nearly the same, the measured radial velocity from the Sun is very close to the radial velocity relative to the Galactic center.

The velocity of this star is so large that it greatly exceeds the escape velocity from the Galaxy; hence, this star is gravitationally unbound to the Milky Way. Within 4 years after this first discovery, about 15 more such hypervelocity stars were discovered, all of them early-type stars (O- or B-stars) with Galactic rest-frame velocities in excess of the escape velocity at their respective distance from the Galactic center. Hence, they will all escape the gravitational potential of the Galaxy. Furthermore, a larger number of stars have been detected whose velocity in the Galactic frame exceeds ∼ 300 km∕s but is most likely not large enough to let them escape from the gravitational field of the Galaxy—i.e., these stars are on bound orbits. In a sample of eight of them, all were found to move away from the Galactic center. This indicates that their lifetime is considerable smaller than their orbital time scale (because otherwise, if they could survive for half an orbital period, one would expect to find also approaching stars), yielding an upper bound on their lifetime of 2 Gyr. Therefore, these stars are most likely on the main sequence.

Acceleration of hypervelocity stars. The fact that the hypervelocity stars are gravitationally unbound to the Milky Way implies that they must have been accelerated very recently, i.e., less than a crossing time through the Galaxy ago. In addition, since they are early-type stars, they must have been accelerated within the lifetime of such stars. The acceleration mechanism must be of gravitational origin and is related to the dynamical instability of N-body systems, with N > 2. A pair of objects will orbit in their joint gravitational field, either on bound orbits (ellipses) or unbound ones (gravitational scattering on hyperbolic orbits); in the former case, the system is stable and the two masses will orbit around each other literally forever. If more than two masses are involved this is no longer the case—such a system is inherently unstable. Consider three masses, initially bound to each other, orbiting around their center-of-mass. In general, their orbits will not be ellipses but are more complicated; in particular, they are not periodic. Such a system is, mathematically speaking, chaotic. A chaotic system is characterized by the property that the state of a system at time t depends very sensitively on the initial conditions set at time t _i < t. Whereas for a dynamically stable system the positions and velocities of the masses at time t are changed only a little if their initial conditions are slightly varied (e.g., by giving one of the masses a slightly larger velocity), in a chaotic, dynamically unstable system even tiny changes in the initial conditions can lead to completely different states at later times. Any N-body system with N > 2 is dynamically unstable.

Back to our three-body system. The three masses may orbit around each other for an extended period of time, but their gravitational interaction may then change the state of the system suddenly, in that one of the three masses attains a sufficiently high velocity relative to the other two and may escape to infinity, whereas the other two masses form a binary system. What was a bound system initially may become an unbound system later on. This behavior may appear unphysical at first sight—where does the energy come from to eject one of the stars? Is this process violating energy conservation?

Of course not! The trick lies in the properties of gravity: a binary has negative binding energy, and the more negative, the tighter the binary orbit is. By three-body interactions, the orbit of two masses can become tighter (one says that the binary ‘hardens’), and the corresponding excess energy is transferred to the third mass which may then become gravitationally unbound. In fact, a single binary of compact stars can in principle take up all the binding energy of a star cluster and ‘evaporate’ all other stars.

Fig. 2.51

The minimum velocity in the Galactic rest frame is plotted against the distance from the Galactic center, for a total of 37 stars. The star symbols show hypervelocity stars, whereas circles are stars which are possibly on gravitationally bound orbits in the Galaxy. The long- and short-dashed curves indicate the escape velocity from the Milky Way, as a function of distance, according to two different models for the total mass distribution in the Galaxy. The dotted curves indicate constant travel time of stars from the Galactic center to a given distance with current space velocity, labeled by this time in units of 10⁶ yr. The distances are estimated assuming that the stars are on the main sequence, whereas the error bars indicate the plausible range of distances if these stars were on the blue horizontal branch. Source: W.R. Brown, M.J. Geller & S.J. Kenyon 2012, MMT Hypervelocity Star Survey. II. Five New Unbound Stars, ApJ 751, 55, p. 5, Fig. 3. ©AAS. Reproduced with permission

This discussion then leads to the explanation of hypervelocity stars. The characteristic escape velocity of the ‘third mass’ will be the orbital velocity of the three-body system before the escape. The only place in our Milky Way where orbital velocities are as high as that observed for the hypervelocity stars is the Galactic center. In fact, the travel time of a star with current velocity of ∼ 600 km∕s from the Galactic center to Galacto-centric distances of ∼ 80 kpc is of order 10⁸ yr (see Fig. 2.51), slightly shorter than the main-sequence lifetime of a B-star. Furthermore, most of the bright stars in the central 1″ of the Galactic center region are B-stars. Therefore, the immediate environment of the central black hole is the natural origin for these hypervelocity stars. Indeed, long before their discovery the existence of such stars was predicted. When a binary system gets close to the black hole, this three-body interaction can lead to the ejection of one of the two stars into an unbound orbit, whereas the other star gets bound to the black hole. This is considered the most plausible explanation for the presence of young stars (like the B-stars of the S-star cluster) near to the black hole. Thus, the existence of hypervelocity stars can be considered as an additional piece of evidence for the presence of a central black hole in our Galaxy.

For one of the hypervelocity stars, the time to travel from the Galactic center to its current position is estimated to be much longer than its main sequence lifetime, by a factor of ∼ 3. Given that it is located just 16^∘ away from the Large Magellanic Cloud, it was suggested that it had been ejected from there. However, for this star a proper motion was measured with HST, and its direction is fully compatible with coming from the Galactic center, ruling out an LMC origin. Therefore, that star is not a main sequence star, but most likely a so-called blue straggler.

The acceleration of hypervelocity stars near the Galactic center may not be the only possible mechanism. Another suggested origin can be related to the possible existence of intermediate black holes with $M_{\bullet } \sim 10^{3}M_{\odot }$ , either at the center of dense star clusters or as freely propagating in the Milky Way, and may be the relics of earlier accretion events of low-mass galaxies.

Hypervelocity stars are not the only fastly moving stars in the Milky Way, but there is a different population of runaway stars. These stars are created through supernova explosions in binaries. Let us consider a binary, in which the heavier star (the primary) undergoes a supernova explosion, possibly leaving behind a neutron star. During the explosion, the star expels the largest fraction of its mass, on a time-scale that is short compared to the orbital period of the binary, due to the high expansion velocity. Thus, almost instantaneously, the system is transformed into one where the primary star has lost most of its mass. Given that the velocity of the secondary star did not change through this process, thus being the orbital velocity corresponding to the original binary, this velocity is now far larger than the orbital velocity of the new binary. Therefore, the system of secondary and the neutron star are no longer gravitationally bound, and they will both separate, with a velocity similar to the original orbital velocity. For close binaries, this can also exceed 100 km∕s, and is the origin of the high space velocities observed for pulsars. However, these runaway stars can hardly be confused with hypervelocity stars, since they are rare and are produced near the Galactic disk.

2.7 Problems

2.1. Angular size of the Moon. The diameter of the Moon is 3476 km, and its mean distance from Earth is about 385 000 km. Calculate the angular diameter of the Moon as seen on the sky. What fraction of the full sky does the Moon cover?

2.2. Helium abundance from stellar evolution. Assume that the baryonic matter M of a galaxy, such as the Milky Way, consisted purely of hydrogen when it was formed. In this case, all heavier elements must have formed from nuclear fusion in the interior of its stellar population. Assume further that the total luminosity L of the galaxy is caused by burning hydrogen into helium, and let this luminosity be constant over the total lifetime of the galaxy, here assumed to be 10¹⁰ yr, with a correspondingly constant baryonic mass-to-light ratio of $M/L = 3M_{\odot }/L_{\odot }$ . What is the mass fraction in helium that would be generated by the nuclear fusion process? Would this fraction be large enough to explain the observed helium abundance of ∼ 27 %?

2.3. Flat rotation curve. We saw that the rotation curve of the Milky Way is flat, V (R) ≈ const. Assume a spherically-symmetric density distribution ρ(r). Determine the functional form of ρ(r) which yields a flat rotation curve.

2.4. The Sun as a gravitational lens. What is the minimum distance a Solar-like star needs to have from us in order to produce multiple images of very distant sources, and how large would the achievable image splitting be? Make use of the fact that the angular diameter of the Sun is 32′ on average.

2.5. Kepler rotation around the Galactic center black hole. We have mentioned that the Galactic center hosts a star cluster with a characteristic velocity dispersion of ∼ 55 km∕s at r ≳ 4 pc. How does this velocity compare with the circular velocity of an object around the central SMBH? Make use of the fact that $\sqrt{ GM_{\odot }/c^{2}} = 1.495\,\mathrm{km}$ , the so-called gravitational radius corresponding to a Solar mass.

2.6. Superluminal motion through scattering. Assume that there is a (infinitely thin) sheet of scattering material between us and the Galactic center (GC). Let that screen be perpendicular to the line-of-sight to the GC, and have a distance D from the GC, so that our distance to this screen is $D_{\mathrm{sc}} = R_{0} - D$ . A light flash at the GC will be seen in scattered light as a ring whose radius changes in time. Calculate the radius R(t) of this ring, and determine its apparent velocity dR∕dt. Can that be larger than the velocity of light? Assume that the opening angle of the ring, as seen both by the GC and by us, is small, so that R∕D ≪ 1, R∕D _sc ≪ 1. Furthermore, assume that the screen is close to the Galactic center, so that D ≪ R ₀. Can you get a similar effect from a scattering screen behind the Galactic center?

Footnotes

The equatorial coordinates are defined by the direction of the Earth’s rotation axis and by the rotation of the Earth. The intersections of the Earth’s axis and the sphere define the northern and southern poles. The great circles on the sphere through these two poles, the meridians, are curves of constant right ascension α. Curves perpendicular to them and parallel to the projection of the Earth’s equator onto the sky are curves of constant declination δ, with the poles located at δ = ±90^∘.

In general, since the star also has a spatial velocity different from that of the Sun, the ellipse is superposed on a linear track on the sky; this linear motion is called proper motion and will be discussed below.

To be precise, the Earth’s orbit is an ellipse, and one astronomical unit is its semi-major axis, being 1 AU = 1. 496 × 10¹³ cm.

i.e., to the main sequence in a color-magnitude diagram in which absolute magnitudes are plotted.

With what we have just learned we can readily answer the question of why the sky is blue and the setting Sun red.

This notation scheme (Type Ia, Type II, and so on) is characteristic for phenomena that one wishes to classify upon discovery, but for which no physical interpretation is available at that time. Other examples are the spectral classes of stars which are not named in alphabetical order nor according to their mass on the main sequence; or the division of Seyfert galaxies into Type 1 and Type 2. Once such a notation is established, it often becomes permanent even if a later physical understanding of the phenomenon suggests a more meaningful classification.

Pulsars are sources which show a very regular periodic radiation, most often seen at radio frequencies. Their periods lie in the range from ∼ 10⁻³ s (milli-second pulsars) to ∼ 5 s. Their pulse period is identified as the rotational period of the neutron star—an object with about one Solar mass and a radius of ∼ 10 km. The matter density in neutron stars is about the same as that in atomic nuclei.

The name of a supernova is composed of the year of explosion, and a single capital letter or two lower case letters. The first detected supernova in a year gets the letter ‘A’, the second ‘B’ and so on; the 27th then obtains an ‘aa’, the 28th an ‘ab’ etc. Hence, SN 1987A was the first one discovered in 1987.

Hii-regions are nearly spherical regions of fully ionized hydrogen (thus the name Hii region) surrounding a young hot star which photoionizes the gas. They emit strong emission lines of which the Balmer lines of hydrogen are strongest.

These energies should be compared with those reached in particle accelerators: the LHC at CERN reaches ∼ 10 TeV = 10¹³ eV. Hence, cosmic accelerators are much more efficient than man-made machines.

Shock fronts are surfaces in a gas flow where the parameters of state for the gas, such as pressure, density, and temperature, change discontinuously. The standard example for a shock front is the bang in an explosion, where a spherical shock wave propagates outwards from the point of explosion. Another example is the sonic boom caused, for example, by airplanes that move at a speed exceeding the velocity of sound. Such shock fronts are solutions of the hydrodynamic equations. They occur frequently in astrophysics, e.g., in explosion phenomena such as supernovae or in rapid (i.e., supersonic) flows such as those we will discuss in the context of AGNs.

The Pierre Auger Observatory in Argentina combines 1600 surface detectors for the detection of particles from air showers, generated by cosmic rays hitting the atmosphere, with 24 optical telescopes measuring the optical light produced by these air showers. The detectors are spread over an area of 3000 km², with a spacing between detectors of 1. 5 km, small enough to resolve the structure of air showers which is needed to determine the direction of the incoming cosmic ray. Starting regular observations in 2004, Auger has already led to breakthroughs in cosmic ray research.

In addition to the two-photon annihilation, there is also an annihilation channel in which three photons are produced; the corresponding radiation forms a continuum spectrum, i.e., no spectral lines.

The determinant in (2.86) is a generalization of the derivative in one spatial dimension to higher dimensional mappings. Consider a scalar mapping y = y(x); through this mapping, a ‘small’ interval Δ x is mapped onto a small interval Δ y, where Δ y ≈ (dy∕dx) Δ x. The Jacobian determinant occurring in (2.86) generalizes this result to a two-dimensional mapping from the lens plane to the source plane.

The expression ‘microlens’ has its origin in the angular scale (2.89) that was discussed in the context of the lens effect on quasars by stars at cosmological distances, for which one obtains image splittings of about one microarcsecond; see Sect. 5.4.1.

These parallax events in addition prove that the Earth is in fact orbiting around the Sun—even though this is not really a new insight….

Masers are regions of stimulated non-thermal emission which show a very high surface brightness. The maser phenomenon is similar to that of lasers, except that the former radiate in the microwave regime of the spectrum. Masers are sometimes found in the atmospheres of active stars.

One problem in the combined analysis of data taken in different wavelength bands is that astrometry in each individual wavelength band can be performed with a very high precision—e.g., individually in the radio and the IR band—however, the relative astrometry between these bands is less well known. To stack maps of different wavelengths precisely ‘on top of each other’, knowledge of exact relative astrometry is essential. This can be gained if a population of compact sources exists that is observable in both wavelength domains and for which accurate positions can be measured.

Prev Next

2. The Milky Way as a galaxy