I do not consider my birth date an especially riveting conversational opener. That may be, however, because I have not spent enough time in the company of men like Jerome Carter. I had just sat down for lunch with him and his wife Pamela at their home in Scottsdale, Arizona, when it came out: 22 November.

‘Waaaooooooow!’ said Pamela, a 57-year-old former air stewardess, who was wearing a pretty pink top and a denim skirt.

Jerome looked at me. In a serious tone he confirmed her enthusiasm: ‘You have got a very good number there.’

Jerome, who is aged 53, does not look like your average mystic. He was dressed in an orange Hawaiian shirt and white shorts, his strong frame reflecting previous careers as a karate champion and international bodyguard. So what was so good about 22/11, I asked?

‘Well, 22 is a master number. So is 11. There are only four master numbers: 11, 22, 33 and 44.’

Jerome has a distinguished face, with strong smile lines and a shiny bald dome. He also has a wonderfully musical voice, part sports commentator, part rapping MC: ‘You were born on the twenty-second,’ he said. ‘It is no accident that our first president was born on the twenty-second. Two and two equals what? Four. We elect our presidents when? Every four years. We pay our taxes in the fourth month. Everything in the United States is four. Everything. Our first navy had 13 ships, 1 and 3 equals 4. We used to have 13 colonies, 1 and 3 equals 4. There were 13 signers of the Declaration of Independence. Four. Where were they standing at? 1300 Locust Street. Four!

‘Number four controls money. You were born under it. It’s a very powerful number. The number four is the square, so it involves law, structure, government, organization, journalism, construction.’

He was beginning to hit his stride: ‘That’s how I told O.J. he was going to walk. I looked at his lawyers. All of his lawyers were born under the number four. Johnny Cochran, born on the twenty-second, 2 and 2 equals 4. F. Lee Bailey, born on the thirteenth. 1 and 3 equals 4. Barry Scheck, born on the fourth. Robert Shapiro, born on the thirty-first, 3 and 1 equals 4. He had four lawyers born under the number four. The verdict came down when? Four p.m. OK? Hitler would have walked!

‘As Mike Tyson said when I did his numbers, when it’s the time with these numbers, even your mistakes turn out good.’

Jerome is a professional numerologist. He believes numbers express qualities, not just quantities. His gift, he said, is that he can use this understanding to gather insights about people’s personalities and even predict the future. Actors, musicians, athletes and corporations pay good money for his advice. ‘Most numerologists are poor. Most psychics are poor,’ he said. ‘Which makes no sense.’ Jerome, on the other hand, lives in a beautiful home in a luxury condo with thee $25,000 motorbikes in the garage.

Birth dates are an obvious source of numbers from which to derive character traits. So are names, since words can be broken down into letters each assigned a number value. ‘Puff Daddy was about to go to jail,’ he said. ‘Puff Daddy had bad relationships. I changed his name to P. Diddy. Then when he wanted to settle down, I changed his name to – Diddy. These were my suggestions and he took them. Jay-Z wanted to marry Beyoncé. I told him he needs to go back to his original name. He went back to Shawn Carter.’

I asked Jerome if he had any recommendations for me.

‘What’s your full name?’ he said.

‘Alexander Bellos, but everyone calls me Alex.’

‘What a bummer.’ He paused for dramatic effect.

‘Is Alexander better?’ I asked.

He boomed: ‘Let us just say that one of the greatest men that walked this Earth was not called Alex the Great.

‘I’m just telling you. I have talked to people named Alex before. Just on a simple basis: the first letter of the name is very important. “A’ is 1. You’ve already got that with Alex. But with Alexander you end with an “r”. “R” equals 9. So the first and the last letters of your name are 1 and 9. Alpha and omega. The beginning and ending. Now let’s take the first and the last letter of Alex. Just the sound of “x”.’ He pronounced it ‘ekkss’ with a grimace that looked like he was about to vomit. ‘Do you want to use that? I wouldn’t. I would never go by Alex.

‘God said a good name is rather to be chosen than riches of gold! He didn’t say a nickname is rather to be chosen!’

‘Alex is not a nickname,’ I protested. ‘It’s an abbreviation.’

‘Why are you fighting it, Alexander?’

Jerome then asked for my pad and scribbled out the following table:

This, he explained, showed which numbers corresponded to which letters. He took his fingers to the first column: ‘Letters that equal one are A, J, S. Allah, Jehovah, Jesus, Saviour, Salvation. Two is the number of diplomats, ambassadors. Two gives good advice, two you love, you’re a team player, that’s B, K and T, that’s why if you go to a Burger King you can have it your way. Number three controls radio, TV, entertainment and numerology. C, L, U. Of course, you go into radio and television, you don’t have a clue.’ He gave me an ironic wink. ‘But if you learn numerology, it will open you up to the clue of life. Number four: D, M, V. How many wheels on a car? Where do you get the licence? The Department of Motor Vehicles. Five is halfway between 1 and 10: E, N and W. Five is the number of change. If you scramble the letters you get ‘new’. Six is the number of Venus, love, family, community. When you see a beautiful woman, what do you see? A FOX. Seven is the number of spirituality. Jesus was born on the twenty-fifth, 2 and 5 equals 7. Eight is the number of business, finance, commerce, money. Where do you keep the money? In the headquarters. Nine is the only one that has two letters. I and R. You ever talked to a Jamaican? Everythg is irie, man.’

On conclusion he put down his pen and looked me full in the face: ‘This,’ he said, ‘is Jerome Carter’s method of the Pythagorean system.’

 

Pythagoras is the most famous name in mathematics, entirely due to his theorem about triangles. (More about that later.) He is credited with other contributions, though, such as the discovery of ‘square numbers’. Imagine, as was common practice, counting with pebbles. (The Latin for pebble is calculus, which explains the origin of the word ‘calculate’.) When you make a square array in which pebbles are placed equally apart in rows and columns, a two-row/ column square requires four pebbles, and a three-row/column square requires nine. In other words, multiplying the number n by itself is equivalent to working out the number of pebbles in a square array with n rows and columns. The idea is so instinctive that the term ‘square’ to describe self-multiplication has stuck.

Pythagoras observed some excellent patterns in his squares. He saw that the number of pebbles used in the 2 square, 4, was the sum of 1 and 3, while the number used in the 3 square, 9, was the sum of 1 and 3 and 5. The 4 square has 16 pebbles – or, 1 + 3 + 5 + 7. In other words, the square of the number n is the sum of the first n odd numbers. This can be seen by looking at how you construct a pebble square:

Another pattern Pythagoras discovered relates to music. One day, according to legend, as he walked past a smithy and heard clinking hammer sounds coming from inside, he noticed that the pitch of the clinking changed depending on the weights of the anvils. This provoked him to investigate the relationship between the pitch of a vibrating string and its length. This in turn led him to the realization that if the length of a string is halved, the pitch increases by an octave. Other harmonies occur when the string is divided in the ratios 3:2 and 4:3, and so on.

Pythagoras was entranced by the numerical patterns he found in nature, believing that the secrets of the universe could be understood only through mathematics. Yet rather than seeing maths merely as a tool to describe nature, he saw numbers as somehow the essence of nature – and he tutored his flock to revere them. For Pythagoras was not just a scholar. He was the charismatic leader of a mystical sect devoted to philosophical and mathematical contemplation, the Pythagorean Brotherhood, which was a combination of health farm, boot camp and ashram. Disciples had to obey strict rules, such as never urinating towards the sun, never marrying a woman who wears gold jewellery, and never passing an ass lying in the street. So select was the group that those wishing to join the Brotherhood had to go through a five-year probationary period, during which they were allowed to see Pythagoras only from behind a curtain.

In the Pythagorean spiritual cosmos, ten was divine not for any reason to do with fingers or toes, but because it was the sum of the first four numbers (1 + 2 + 3 + 4 = 10), each of which symbolized one of the four elements: fire, air, water and earth. The number 2 was female, 3 was male, and 5 – their union – was sacred. The crest of the Brotherhood was the pentagram, or five-pointed star. While the idea of worshipping numbers may now seem bizarre, it perhaps reflects the scale of wonderment at the discovery of the first fragments of abstract mathematical knowledge. The excitement of learning that there is order in nature, when previously you were not aware that there was any at all, must have felt like a religious awakening.

Pythagoras’s spiritual teachings were more than just numerological. They included a belief in reincarnation, and he was probably a vegetarian. In fact, his dietary requirements have been hotly debated for more than 2000 years. The Brotherhood famously forbade ingestion of the small, round, black fava bean, and one account of Pythagoras’s death has him fleeing attackers when he came to a field of fava beans. As the story goes, he preferred to be captured and killed rather than tread on them. The reason the beans were sacred, according to one ancient source, was that they sprouted from the same primordial muck as humans did. Pythagoras had proved this by showing that if you chew up a bean, crush it with your teeth, and then put it for a short while in the sun, it will begin to smell like semen. A more recent hypothesis was that the Brotherhood was just a colony for those with hereditary fava-bean allergies.

 

Pythagoras lived in the sixth century BC. He did not write any books. All we know about him was written many years after he died. Though the Brotherhood was lampooned in ancient Athenian comic theatre, by the beginning of the Christian Era Pythagoras himself was seen in a rather favourable light, viewed as being a unique genius; his mathematical insights making him the intellectual forefather of the great Greek philosophers. Miracles were attributed to him, and some authors, rather oddly, claimed that he had a thigh made of gold. Others wrote that he once walked across a river, and the river called out to him, loud enough for all to hear, ‘Greetings, Pythagoras’. This posthumous myth-making has parallels with the story of another Mediterranean spiritual leader and, in fact, Pythagoras and Jesus were temporarily religious rivals. As Christianity was taking root in Rome in the second century CE, the empress Julia Domna encouraged her citizens to worship Apollonius of Tyna, who claimed he was Pythagoras reincarnated.

Pythagoras has a dual and contradictory legacy: his mathematics and his anti-mathematics. Maybe, in fact, as some academics now suggest, the only ideas that can be correctly attributed to him are the mystical ones. Pythagorean esotericism has been a constant presence in Western thought since antiquity, but was especially in vogue during the Renaissance, thanks to the rediscovery of a poem of ‘self-help’ maxims written around the fourth century bc called The Golden Verses of Pythagoras. The Pythagorean Brotherhood was the model for many occult secret societies and influenced the creation of freemasonry, a fraternal organization with elaborate rituals that is believed to have almost half a million members in the UK alone. Pythagoras also inspired the ‘founding mother’ of Western numerology, Mrs L. Dow Balliett, an Atlantic City housewife who wrote the book The Philosophy of Numbers in 1908. ‘Pythagoras said the Heavens and Earth vibrate to the single numbers or digits of numbers,’ she wrote, and she proposed a system of fortune-telling in which each letter of the alphabet corresponded with a number from 1 to 9. By adding up the numbers of the letters in a name, she asserted, personality traits could be divined. I tested this idea on myself. ‘Alex’ is 1 + 3 + 5 + 6 = 15. I completed the process by adding the two digits of the answer, getting 1 + 5 = 6. This gives me a name vibration of six, which means that I ‘should always be dressed with care and precision; be fond of dainty effects and colors, lifting yourcolors of orange, scarlet and heliotrope into their lighter shades, yet always keeping their true tones’. My gems are topaz, diamond, onyx and jasper, while my mineral is borax, and my flowers are tuberose, laurel and chrysanthemum. My odour is japonica.

Numerology, of course, is now an established dish on the buffet of modern mysticism, with no shortage of gurus willing to advise on lottery numbers or speculate on the portent of a prospective date. It sounds like harmless fun – and I enjoyed my conversation with Jerome Carter immensely – yet giving numbers spiritual significance can also have sinister consequences. In 1987, for example, the military government in Burma issued new banknotes with a face value divisible by nine – for the sole reason that nine was the ruling general’s favourite number. The new notes helped precipitate an economic crisis, which led to an uprising on 8 August 1988 – the eighth of the eighth of ’88. (Eight was the anti-dictatorship movement’s favourite number.) The protest was violently put down, however, on 18 September: in the ninth month, on a day divisible by nine.

 

Pythagoras’s Theorem states that for any right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Its words are imprinted in my brain like an old nursery rhyme or Christmas carol; the phrase is nostalgic and comforting independently of its meaning.

The hypotenuse is the side opposite the right angle, and a right angle is a quarter turn. The theorem is the smash hit of basic geometry, the first truly thought-provoking mathematical concept we are taught at school. What I find exciting about it is how it reveals a deep connection between numbers and space. Not all triangles are right-angled, but when they are, the squares of two of the sides must equal the square of the third. Likewise, the theorem holds in the other direction too. Take any three numbers. If the square of two of them equals the square of the third then you can construct a right-angled triangle out of lengths of those sizes.

In some commentaries about Pythagoras it is said that before he founded the Brotherhood he travelled on a fact-finding mission to Egypt. If he had spent any time on an Egyptian building site he would have seen that the labourers used a trick to create a right angle that was an application of the theorem that would later gain his name. A rope was marked with knots spread out at a distance of 3, 4 and 5 units. Since 3² + 4² = 5², when the rope was stretched around three posts, with a knot at each post, it formed a triangle with one right angle.

Pythagoras’s Theorem.

Rope-stretching was the most convenient way to achieve right angles, which were needed so that bricks, or giant stone blocks such as those used to construct the Pyramids, could be stacked next to and on top of each other. (The word hypotenuse comes from the Greek for ‘stretched against’.) The Egyptians could have used many other numbers in addition to 3, 4 and 5 to get real right angles. In fact, there is an infinite number of numbers a, b and c such that a2 + b² = c². They could have marked out their rope into sections of 5, 12 and 13, for example since 25 + 144 = 169, or 8, 15 and 17, since 64 + 225 = 289, or even 2772, 9605 and 9997 (7,683,984 + 92,256,025 = 9940,009) though that would hardly have been practical. The numbers 3, 4, 5 are best suited to the task. As well as being the triple with the lowest value, it is also the only one whose digits are consecutive integers. Due to its rope-stretching heritage, the right-angled triangle with sides that are in the ratio 3:4:5 is known as an Egyptian triangle. It is a pocket-sized right-angle-generating machine that is a jewel of our mathematical patrimony, an intellectual artefact of great power, elegance and concision.

The Egyptian equivalent of a set square was a rope divided in the ratio 3:4:5, which provides a right angle when tied around three posts.

The squares mentioned in Pythagoras’s Theorem can be understood as numbers and also as pictures – literally the squares drawn on the sides of the triangle. Imagine that in the following image the squares are made of gold. You are not engaged to a member of the Pythagorean Brotherhood, so acquiring gold is desirable. Either you can take the two smaller squares, or you can have the one largest square. Which would you prefer?

The mathematician Raymond Smullyan said that when he put this question to his students, half the class wanted the big single square and the other half wanted the double. Both sides were stunned when he told them that it would make no difference.

This is true because, as the theorem states, the combined area of the two smaller squares is equal to the area of the large square. All right-angled triangles can be extended in this way to produce three squares such that the area of the large one can be divided exactly into the areas of the two smaller ones. It is not the case that the square on the hypotenuse is sometimes the sum of the squares of the other two sides, and sometimes not. The fit is perfect at all times.

It is not known if Pythagoras really discovered his theorem, even though his name has been attached to it since classical times. Whether or not he did, it vindicates his world-view, demonstrating a remarkable harmony in the mathematical universe. In fact, the theorem reveals a relationship between more than just the squares on the sides of a right-angled triangle. The area of a semicircle on the hypotenuse, for example, is equal to the sum of the areas of the semicircles on the other two sides. A pentagon on the hypotenuse is equal to the sum of pentagons on the other two sides, and this holds for hexagons, octagons and, indeed, any regular or irregular shape. If, say, three Mona Lisas were drawn on a right-angled triangle, then the area of big Mona is equal to the combined area of the two smaller ones.

For me, the real delight in Pythagoras’s Theorem is in the realization of why it must be true. The simplest proof is as follows. It dates back to the Chinese, possibly to before even Pythagoras was born, and is one of the reasons why many doubt he came up with the theorem in the first place.

Stare at the two squares for a while before reading on. Square A is the same size as square B, and all the right-angled triangles inside the square are also the same size. Because the squares are equal, the white area inside them is also equal. Now, note that the big white square inside square A is the square of the hypotenuse of the riht-angled triangle. And the smaller white squares inside square B are the squares of the other two sides of the triangle. In other words, the square of the hypotenuse is equal to the square of the other two sides. Voilà.

Since we can construct a square like A and B for any shape or size of right-angled triangle, the theorem must be true in all cases.

The thrill of maths is the moment of instant revelation, from proofs such as this, when suddenly everything makes sense. It is immensely satisfying, an almost physical pleasure. The Indian mathematician Bhaskara was so taken by this proof that underneath a picture of it in his twelfth-century maths book Lilavati, he wrote no explanation, just the word ‘Behold!’

 

There are many other proofs of Pythagoras’s Theorem, and a particularly lovely one is found in the figure overleaf, credited to the Arabic mathematician Annairizi, and dated around 900 CE. The theorem is contained within the repeating pattern. Can you spot it? (If you can’t, some help is included as an appendix.)

In his 1940 book The Pythagorean Proposition, Elisha Scott Loomis published 371 proofs of the theorem, devised by a surprisingly diverse collection of people. One dating to 1888 was attributed to E.A. Coolidge, a blind girl, another to Ann Condit, a 16-year-old high-school student, dating to 1938, while others were attributed to Leonardo da Vinci and US President James A. Garfield. Garfield had stumbled on his proof during some mathematical amusements with colleagues when he was a Republican congressman. ‘We think it something on which the members of both houses can unite without distinction of party,’ he said when the proof was first published in 1876.

The diversity of proofs is a testament to the vitality of maths. There is never a ‘right’ way to attack a maths problem, and it’s intriguing to chart the different routes that different minds have taken in finding solutions. Above opposite are three different proofs from three different eras: one by Liu Hui, a Chinese mathematician from the third century ce, one by Leonardo da Vinci (1452–1519) and the third by Henry Dudeney, Britain’s most famous puzzlist, dated 1917. Both Liu Hui and Dudeney’s are ‘dissection proofs’ in which the two small squares are divided into shapes that can be reassembled perfectly in the big square. Leonardo’s needs a little more thought. (If you need help, see the appendix again.)

A particularly dynamic proof was devised by the mathematician Hermann Baravalle, shown below opposite. There is something more organic about this one – it shows how the big square, like an amoeba, divides itself into the two smaller ones. At each stage, the area shaded is the same. The only step that isn’t obvious is step 4. When a parallelogram is ‘sheared’, or moved in such a way that preserves the base and altitude, its area stays the same.

Baravalle’s proof is similar to the most established one in mathematical literature, that set out by Euclid around 300 BC.

Euclid, the next most famous Greek mathematician after Pythagoras, lived in Alexandria, the city founded by the man who never abbreviated his name to Alex the Great. His chef-d’œuvre, The Elements, contained 465 theorems that summarized the extent of Greek knowledge at that time. Greek mathematics was almost entirely geometry – derived from their words for ‘earth’ and ‘measurement’ – although The Elements was not concerned with the real world. Euclid was operating in an abstract domain of points and lines. All he allowed in his toolkit was a pencil, a ruler and a compass, which is why they have been the fundamental components of children’s pencil cases for centuries.

Euclid’s first task (Book 1, Proposition 1) was to show that, given any line, he could make an equilateral triangle, i.e. a triangle with three equal sides, with that line as one side:

The Elements , Proposition 1.

He then meticulously progressed from proposition to proposition, revealing a host of properties of lines, triangles and circles. For example, Proposition 9 shows how to ‘bisect’ an angle, that is construct an angle that is exactly half of a given angle. Proposition 32 states that the internal angles of a triangle always add up to two right angles, or 180 degrees. The Elements is a magnum opus of pedantry and rigour. Nothing is ever assumed. Every line follows logically from the line before. Yet from only a few basic axioms, Euclid amassed an impressive body of compelling results.

The grand finale of the first book is Proposition 47. The commentary from a 1570 edition of the first English translation reads: ‘This most excellent and notable Theoreme was first invented of the greate philosopher Pithagoras, who for the exceeding ioy conceived of the invention thereof, offered in sacrifice an Oxe, as recorde Hierone, Proclus, Lycius, & Vitruvius. And it hath bene commonly called of barbarous writers of the latter time Dulcarnon.’ Dulcarnon means two-horned, or ‘at wit’s end’ – possibly because the diagram of the proof has two horn-like squares, or possibly because understanding it is indeed horribly difficult.

There is nothing pretty about Euclid’s proof of Pythagoras’s Theorem. It is long, meticulous and convoluted, and requires a diagram full of lines and superimposed triangles. Arthur Schopenhauer, the nineteenth-century German philosopher, said it was so unnecessarily complicated that it was a ‘brilliant piece of perversity’. To be fair to Euclid, he was not trying to be playful (as was Dudeney), or aesthetic (as was Annairizi) or intuitive (as was Baravalle). Euclid’s driving concern was the of his deductive system.

While Pythagoras saw wonder in numbers, Euclid in The Elements reveals a deeper beauty, a watertight system of mathematical truths. On page after page he demonstrates that mathematical knowledge is of a different order than any other. The propositions of The Elements are true in perpetuity. They do not become less certain, or indeed less relevant with time (which is why Euclid is still taught at school and why Greek playwrights, poets and historians are not). The Euclidean method is awe-inspiring. The seventeenth-century English polymath Thomas Hobbes is said to have glanced at a copy of The Elements that lay open in a library when he was a 40-year-old man. He read one of the propositions and exclaimed: ‘By God, this is impossible!’ So, he read the previous proposition, and then the one before that, and so on, until he was convinced it all made sense. In the process, he fell in love with geometry for the certainty it prescribed, and the deductive approach influenced his most famous works of political philosophy. Since The Elements, logical reasoning has been the gold standard of all human enquiry.

 

Euclid started off by carving up two-dimensional space into the family of shapes known as polygons, which are those shapes made from only straight lines. With his compass and straightedge he was able to construct not just an equilateral triangle, but also a square, a pentagon and a hexagon. Polygons for which every side has the same length and the angles between the sides are all equal are called regular polygons. Interestingly, Euclid’s method, however, is not effective for all of them. The heptagon (seven sides), for example, cannot be constructed with a compass and straightedge. The octagon is constructible, but then the nonagon again is not. Meanwhile, the staggeringly complex regular polygon that has 65,537 sides is constructible, and in fact has been constructed. (It was chosen because the number is equal to 2¹⁶ + 1). In 1894 it took Johann Gustav Hermes, a German mathematician, ten years to do it.

Regular polygons.

One of Euclid’s pursuits was to investigate the three-dimensional shapes that can be made from joining identical regular polygons together. Only five shapes fit the bill: the tetrahedron, the cube, the octahedron, the icosahedron and the dodecahedron, the quintet known as the Platonic solids since Plato wrote about them in the Timaeus. He equated them with the four elements of the universe plus the heavenly space that surrounds them all. The tetrahedron was fire; the cube, earth; the octahedron, air; the icosahedron, water; and the dodecahedron, the encompassing dome. The Platonic solids are particularly interesting because they are perfectly symmetrical. Twist them, roll them, invert them or flip them and they always stay the same.

The Platonic solids.

In the thirteenth and final book of The Elements, Euclid proved why there are only five Platonic solids by working out all the possible solid objects that can be made from regular polygons, starting with the equilateral triangle, and then moving on to squares, pentagons, hexagons and so on. The diagram overleaf shows how he reached his conclusion. To make a solid object from polygons you must alwys have a point where three sides meet, a corner, or what’s called a vertex. When you join three equilateral triangles at a vertex, for example, you get a tetrahedron (A). When you join four, you get a pyramid (B). A pyramid is not a Platonic solid because not all the sides are the same, but by sticking an inverted pyramid on the bottom you get an octahedron, which is. Join five equilateral triangles together and you have the first part of an icosahedron (C). But join six and you get…a flat piece of paper (D). You cannot make a solid angle with six equilateral triangles, so there are no other ways to create a different Platonic solid made up of them. Continuing this procedure with squares, it is evident that there is only one way to join three squares at a corner (E). This will end up as a cube. Join four squares and you get…a flat piece of paper (F). No more Platonic solids here. Similarly, three pentagons together give a solid angle, which becomes the dodecahedron (G). It is impossible to join four pentagons. Three hexagons meeting at the same point lie flat alongside each other (H), so it is impossible to make a solid object out of them. There are no more Platonic solids since it is impossible to join three regular polygons of more than six sides at a vertex.

Using Euclid’s method, many mathematicians after him have asked new questions and made new discoveries. For example, in 1471 the German mathematician Regiomontanus wrote a letter to a friend in which he posed the following problem: ‘At what point on the ground does a perpendicularly suspended rod appear largest?’ This has been rephrased as the ‘statue problem’. Imagine there is a statue on a plinth in front of you. When you are too close you have to crick your neck and you have a very narrow angle to look up at it. When you are far away, you have to strain your eyes and, again, see it through a very narrow angle. Where, then, is the best place to view it?

Proof that there are only five Platonic solids.

Consider a side-on view of the situation, as in the diagram opposite. We want to find the point on the dotted line, which represents eye level, such that the angle from the point to the statue is greatest. The solution follows from the third book of The Elements, on circles. The angle is largest when a circle that goes through the top and bottom of the statue rests on the dotted line.

The problem is equivalent to that faced by rugby players wanting to know the best distance from the tryline to kick a conversion. If you are too near the opposing tryline the angle is too tight, but if you are too far the angle is also reduced. Where is the optimum position? Here we need to take an aerial view of the pitch and draw a similar diagram. The point on the dotted line of allowed kick spots that subtends the greatest angle to the posts is precisely the point touched by a circle that passes through both posts and rests on the line.

Regiomontanus’s statue and rugby problem.

Perhaps the most stunning result in Euclidean geometry, though, is one that reveals an astonishing property about triangles. Let’s first consider where the centre of a triangle is. This is a surprisingly unclear issue. In fact, there are four ways we can define the centre of a triangle and they all represent different points (unless the triangle is equilateral, when they all coincide). The first is called the orthocentre, and is the intersection of the lines from each vertex that meet the opposing sides perpendicularly, which are called the altitudes. It is already pretty amazing to think that, for any triangle, the altitudes always meet at the same point.

Construction of the Euler line.

The second is the circumcentre, which is the intersection of the perpendiculars drawn from the halfway points of the sides. Again, it is very neat that these lines will also always meet, whatever triangle you choose.

The third is the centroid, which is the intersection of the lines that go from the vertex to the midpoints of opposing lines. They always meet too. Finally, the midcircle is a circle that passes through the midpoints of each side and also the intersections of the sides and the altitudes. Every triangle has a midcircle, and its centre is the fourth type of middle point a triangle can have.

In 1767 Leonhard Euler proved that for all triangles the orthocentre, the circumcentre, the centroid and the centre of the midcircle are always on the same line. This is mind-blowing. Whatever the shape of a triangle these four points have a dazzlingly uniform relation to each other. The harmony is truly wondrous. Pythagoras would have been most awed.

 

Though this may be hard to fathom these days, The Elements was a literary sensation. Until the twentieth century, it is said to have had more editions printed than any other book except the Bible. This was all the more remarkable since The Elements is no easy read. One edition, however, is worth mentioning for its unorthodox approach in making the text accessible. Oliver Byrne, whose day job was Surveyor of Her Majesty’s Settlements in the Falkland Islands, rewrote Euclid in colour. Instead of the long proofs, he drew illustrations in which angles, lines and areas were marked in geometrical blocks of red, yellow, blue or black. His Elements…in which coloured diagrams and symbols are used instead of letters for the greater ease of learning was published in 1847 and has been described as ‘one of the oddest and most beautiful books of the whole nineteenth century’. In 1851 it was one of the few British books on display at the Great Exhibition, though the public failed to see the excitement. Indeed, Byrne’s publishers went bust in 1853, with more than 75 percent of stock of The Elements unsold. Its high production costs had contributed to the bankruptcy.

Byrne’s illustrated proofs did make Euclid more intuitive, predating colour-coordinated textbooks of recent years. Aesthetically it was also ahead of its time. The gaudy primary colours, asymmetrical layout, angularity, abstract shapes and plentiful empty space anticipated the paintings of many twentieth-century artists. Byrne’s book looks like a tribute to Piet Mondrian, published 25 years before Mondrian was even born.

 

As masterful as the Euclidean method was, it could not solve all problems; some quite simple ones, in fact, are unsolvable using just a compass and ruler. The Greeks suffered for this. In 430 bc Athens was struck by a plague of typhoid. Its citizens consulted the oracle at Delos, who advised them to double the size of Apollo’s altar, which was cube-shaped. Relieved that such an apparey easy task would save them, they constructed a new altar where the sides of the cube were double the length of those of the original altar. Yet by doubling the side of a cube, the volume of the cube increases by two cubed, or eight. Apollo was not happy and made the pestilence worse. The challenge that the god set – that is, given a cube, construct a second cube that has twice the volume – is called the Delian Problem, and it is one of the three classic problems of antiquity that cannot be solved by Euclidean tools. The other two are the squaring of the circle, which is the construction of a square that has the same area as a given circle, and the trisection of an angle, which is the construction of an angle that is a third of a given angle. Realizing why Euclidean geometry cannot solve these problems – and why other methods can – has been a long-time preoccupation of mathematics.

 

The Greeks were not the only people intrigued by the wonders of geometrical shapes. The most sacred object in Islam is a Platonic solid: the Ka’ba, or Cube, is the black palladium at the centre of Mecca’s Sacred Mosque, around which pilgrims walk anticlockwise during the Hajj. (In fact, its dimensions make it just off a perfect cube.) The Ka’ba also marks the point that worshippers must face during daily prayer, wherever they are in the world. Mathematics plays more of a role in Islam than in any other major religion. More than a millennium before the advent of GPS technology, the requirement to face Mecca relied on complicated astronomical calculations – which is one reason why Islamic science was unequalled for almost a thousand years.

Islamic art is epitomized by the ingenious geometrical mosaic arrangements on the walls, ceilings and floors of its sacred buildings, a consequence of the ban on images of people and animals in holy sites. Geometry was thought to express truth beyond what was merely human, much in keeping with the Pythagorean position that the universe reveals itself through mathematics. The symmetries and endless loops that Islamic craftsmen created in their patterns were an allegory of the Infinite, an expression of the sacred, mathematical order of the world.

The beauty of a repeating mosaic pattern lies not so much in the aesthetic appeal of the replicated image as in the effortlessness with which the tiles perfectly fill the space. The better the geometry, the better the art. Working out what shapes will tile a wall so that there are no gaps and no overlaps is quite a mathematical challenge, familiar to anyone who has ever tiled a bathroom floor. It turns out that only three of the regular polygons are able to ‘tessellate’, which is the technical word for covering a plane so that no region is uncovered. These are the equilateral triangle, the square and the hexagon. In fact, a triangle is not required to be equilateral in order to tessellate. The sides can be of any size. For any triangle, all you need to do is join it to an identical triangle placed upside-down, as in the diagram below. The combined shape is a parallelogram. The parallelogram can be joined with identical ones to form a row, and these rows can fit together side by side. This type of tessellation – in which the same pattern repeats endlessly – is called periodic.

Triangle and quadrilateral tessellations.

A square tile will fill a flat surface. That’s obvious. So does any rectangle. That is also a trivial observation – staring at a brick wall is equally the scrutiny of a at’ion of rectangles. What is surprising, however, is that any shape with four sides can also produce periodic tessellations. Draw any four-sided shape. Join this shape with one upside-down, as we did with the triangle above, and you create a six-sided shape, an irregular hexagon, with the property that each of the opposite edges are equal. Since the opposite edges are equal, the shape can be laid in a row such that the edges fit perfectly alongside each other. As the diagram on the previous page shows, this fit works in the direction of each of the sides, and the repeated hexagons cover a plane perfectly.

I said that a periodic tessellation is one that repeats endlessly. There is a more practical definition of periodicity. Imagine a plane extending infinitely in all directions and covered with the triangle tessellation on the previous page. Now imagine making an identical copy of the tessellation on tracing paper and placing it on the plane. Periodicity can be defined as the capacity to lift up the copy, move it along to another position and then to put it back down on the plane so that the pattern of the copy lines up perfectly with the original pattern. We can do this with the triangle tessellation because we can move the copy to the left (or right, or up, or down) by any number of triangles. When the copy is aligned to its new position, the copy is a perfect fit for the tessellation underneath. This definition of periodicity is helpful because it is now easier to explain the concept of nonperiodicity. A nonperiodic tessellation is one that when a copy is made, there is only one position where the copy fits perfectly over the plane – the original position. For example, the tessellation below opposite is nonperiodic. (Imagine that the tessellation goes on for ever, in widening concentric pentagons.) If you made a copy of it, the copy coincides only with the underlying tessellation in one position.

Nonperiodic tessellation.

Many types of tile that can be arranged periodically can also be arranged nonperiodically. The question that tantalized mathematicians in the second half of the twentieth century, however, was whether or not there existed any sets of tiles that could be tiled only nonperiodically. These would be tiles that could cover a plane surface but were incapable of producing repeated patterns. The idea is counter-intuitive – if tiles are so well suited and harmonious that they can tile a plane without leaving any gaps, then it would seem natural that they are able to do so in a regular, repeating way. For a long time it was believed that nonperiodic tiles did not exist.

Then along came Roger Penrose with his kites and darts. In the 1970s, Penrose – a cosmologist – thrilled the maths world when he developed several types of nonperiodic tiles. The simplest were created by judiciously cutting a rhombus in two, to form two different shapes, which he called a kite and a dart. Since any four-sided shape can produce a periodic tessellation, Penrose then had to formulate a rule for how these tiles could be joined that would restrict the patterns they could make to being nonperiodic. He did this by drawing two arcs on each kite and dart and stipulating that tiles must be connected so that like arc always joins with like.

Penrose’s dart and kite can tile only nonperiodically.

The discovery of nonperiodic tiling was an exciting breakthrough for maths, but not as exciting as it would later be for physics and chemistry. In the 1980s researchers were amazed to discover a type of crystal that they did not believe existed. The tiny structure displayed a nonperiodic pattern, behaving in three dimensions just like Penrose’s tiles did in two. The existence of these structures – called quasicrystals – changed the way scientists understood the nature of matter, since it contradicted classical theory that all crystals must have symmetrical lattices derived from the Platonic solids. Penrose may have invented his tiles for fun, but they were unduly prophetic about the natural world.

Half a millennium ago, Islamic geometers might also have understood about non-periodic tessellations. In 2007 Peter J. Lu from Harvard University and Paul J. Steinhardt from Princeton claimed that their studies of mosaics in Uzbekistan, Afghanistan, Iran, Iraq and Turkey showed that the craftsmen had made ‘nearly perfect quasi-crystalline Penrose patterns, five centuries before discovery in the West’. It is possible, therefore, that Islamic mathematics may have been even more advanced than historians of science have traditionally thought.

Hinduism also used geometry to illustrate the divine. Mandalas are symbolic representations of deities and the cosmos. The most complex of these is the Sri Yantra, a figure made up of five triangles pointing down and four pointing up, all overlapping a central point, or bindu. It is said to represent the essential outline of the universal processes of emanation and reabsorption, and is used as a focus for meditation and worship. Constructing it is very imprecise – its structure is enigmatically described in a long poem, but the sacred texts do not give enough detail. Mathematicians are baffled to this day by exactly how it is properly constructed.

 

Another Eastern culture has long embraced the joys of geometric shapes. Origami, the art of paper-folding, evolved from the custom of Japanese farmers thanking the gods at harvest time by making an offering of some of their crops on a piece of paper. Rather than placing the produce on a flat sheet, they would make one diagonal fold in the paper to give the offering a human touch. Origami flourished in Japan over the last few hundred years as an informal pastime, the kind of thing parents did with their children for fun. It fitted in perfectly with the Japanese love of artistic understatement, attention to detail and economy of form.

The Sri Yantra.

Business-card origami sounds like the ultimate Japanese invention, uniting two national passions. In fact, the practice is abhorrent to them. The Japanese see business cards as an extension of the individual, so playing with them is considered grossly offensive, even with origamic intent. When I tried to fold one in a Tokyo restaurant I was almost ejected for my antisocial behaviour. In the rest of the world, however, business-card origami is a modern paper-folding subgenre. It dates back more than a hundred years, to the (now obsolete) practice of visiting-card origami.

A simple example is to fold a business card so that the bottom right corner meets the top left corner, and then fold the overlaps, as shown overleaf. Repeat this with another business card, except this time fold the bottom left to the top right. You now have two pieces that can be slotted together to form a tetrahedron. It is a winning way, so I am told, to hand over your business card during mathematics conferences.

The octahedron can be made from four cards, and an icosahedron with ten of them. It is also easy to make a fourth Platonic solid – the cube. Put two cards on top of each other like a plus sign and fold the flaps as shown above. This creates the shape of a square. Six cards folded in this way slot together to form a cube, although the flaps are on the outside. You need another six cards to slide on to each face in order to make the cube clean.

 

The Zen master of business-card origami is Jeannine Mosely, a software developer from Massachussetts. A few years ago she found herself with 100,000 cards in her garage – she inherited three batches from her colleagues at work, the first time when the company changed its name, the second when the company moved addresses, and then again when it was discovered that the new cards all had a typo. You can make a lot of tetrahedrons with 100,000 business cards. Yet Mosely had much grander ambitions than the Platonic solids. Why limit herself to the ancient Greeks? Had 2000 years of geometry not produced a more exciting 3-D shape? With her resources Mosely felt ready to tackle the ultimate challenge of her art, the Menger sponge.

Before we get to the Menger sponge, I need to introduce the Sierpinski carpet. The bizarre shape was invented by the Polish mathematician Waclaw Sierpinski in 1916. You start with a black square. Imagine it is made of nine identical subsquares, and remove the central one (figure A). Now for each of the remaining subsquares, repeat the operation – that is, imagine they are made of nine subsquares and remove the central one (B). Repeat this process again (C). The Sierpinski carpet is what you get if you continue this process ad infinitum.

In 1926 the Austrian mathematician Karl Menger came up with the idea of a three-dimensional version of the Sierpinski carpet, which is now known as the Menger sponge. You start with a cube. Imagine it is made up of 27 identical subcubes and remove the subcube at the very centre, as well as the 6 subcubes that are in the centre of each of the sides of the original cube. You are left with a cube that looks like it has three square holes drilled through it (D). Treat each of the 20 subcubes that are left like the original cube, and extract 7 of the 27 subcubes (E). Repeat the process again (F) and the block starts to look like it has been devoured by a cluster of geometrically obsessed woodworm.

Thinking inside the box: Jeannine Mosely and her Menger Sponge.

The Menger sponge is a brilliantly paradoxical object. As you continue the iterations of taking out smaller and smaller cubes the volume of the sponge gets smaller and smaller, eventually becoming invisible – as though the woodworm have eaten the whole lot. Yet each iteration of cube removal also makes the surface area of the sponge increase. By taking more and more iterations you can make the surface area larger than any area you want, meaning that as the number of iterations approaches infinity, the surface area of the sponge also approaches infinity. In the limit, the Menger sponge is an object with an infinitely large surface area that is also invisible.

Mosely constructed a level-three Menger sponge – in other words, a sponge after three iterations of cube removal (F). The project took her ten years. She enlisted the help of abut 200 people, and used 66,048 cards. The finished sponge was 4ft 8in high, wide and deep.

‘For a long time I wondered if I was doing something completely and utterly ridiculous,’ she told me. ‘But when I had got it done I stood next to it and realized the scale gave it a grandeur. A particularly wonderful thing is that you can stick your head and shoulders into the model and see this amazing figure from a viewpoint that you have never seen before.’ It was endlessly fascinating to look at because the more she zoomed in, the more she saw the patterns repeating themselves. ‘You simply look at it and it doesn’t need to be explained. You can understand it just by looking at it. It is an idea made solid; math made visual.’ The business-card Menger sponge is a beautifully crafted object that creates an emotional and intellectual response. It belongs just as much to geometry as it does to art.

 

Although origami was originally a Japanese invention, paper-folding techniques also developed independently in other countries. A European pioneer was the German educator Friedrich Fröbel, who used paper-folding in the mid nineteenth century as a way of teaching young children geometry. Origami had the advantage of allowing kindergarten pupils to feel the objects created, rather than just see them in drawings. Fröbel inspired the Indian mathematician T. Sundara Row to publish Geometric Exercises in Paper Folding in 1901, in which he argued that origami was a mathematical method that in some cases was more powerful than Euclid’s. He wrote that ‘several important geometric processes…can be effected much more easily than with the compass and ruler’. But even he did not anticipate just how powerful origami can actually be.

In 1936 Margherita P. Beloch, an Italian mathematician at the University of Ferrara, published a paper that proved that starting with a length L on a piece of paper, she could fold a length that was the cube root of L. She might not have realized it at the time, but this meant that origami could solve the problem given to the Greeks at Delos, where the oracle demanded that the Athenians double the volume of a cube. The Delian Problem can be rephrased as the challenge to create a cube with sides that are – the cube root of two – times the side of a given cube. In origami terms, the challenge is reduced to folding the length from the length 1. Since we can double 1 to get 2 by folding the length 1 on itself, and we can find the cube root of this new length following Beloch’s steps, the problem was solved. It also followed from Beloch’s proof that any angle could be trisected – which cracked the second great unsolvable problem of antiquity. Beloch’s paper, however, remained in obscurity for decades, until, in the 1970s, the maths world began to take origami seriously.

The first published origami proof of the Delian Problem was by a Japanese mathematician in 1980, and angle trisection followed by an American in 1986. The boom of interest stemmed in part from frustration with more than two millennia of Euclidean orthodoxy. The restrictions imposed by Euclid’s limitation to working with only a ruler and compass had narrowed the scope of mathematical enquiry. As it turns out, origami is more versatile than a ruler and compass, for example, in constructing the regular polygons. Euclid was able to draw an equilateral triangle, square, pentagon and hexagon, but recall that the heptagon (which has seven sides) and nonagon (nine) eluded him. Origami can fold heptagons and nonagons relatively easily, although i meets its match with the 11-agon. (Strictly speaking, this is one-fold-at-a-time origami. If multiple folds are allowed any polygon can in theory be constructed, even though a physical demonstration may be so hard as to be impossible.)

Far from being child’s play, origami is now at the cutting edge of maths. Literally. When Erik Demaine was 17 he and his collaborators proved that it is possible to create any shape with straight sides by folding a piece of paper and making just one cut. Once you decide on the shape you want to make, you work out the fold pattern, fold the paper, make the single cut, unfold the paper and the detached shape will fall out. While it might appear that such a result would be of interest only to schoolchildren making increasingly complex Christmas decorations, Demaine’s work has found uses in industry, especially in car airbag design. Origami has connections to protein folding, and now has applications in the most unexpected spheres: in creating arterial stents, robotics, and in the solar panels of satellites.

A guru of modern origami is Robert Lang, who as well as advancing the theory behind paper-folding has turned the pastime into a sculptural art form. A former NASA physicist, Lang has pioneered the use of computers in designing fold patterns to create new and increasingly complex figures. His original figures include bugs, scorpions, dinosaurs and a man playing a grand piano. The fold patterns are almost as beautiful as the finished design.

 

The United States now has as good a claim as Japan does to being at the forefront of origami, partly because origami is so embedded within Japanese society as an informal pursuit that there is more of a barrier to taking it seriously as a science. The cause is not helped by a Monty Pythonesque factionalization between different organizations, each claiming exclusive access to origami’s soul. I was surprised to hear Kazuo Kobayashi, chairman of the International Origami Association, dismiss the work of Robert Lang as elitist: ‘He is doing it for himself,’ he tut-tutted. ‘My origami is about the rehabilitation of the sick and educating children.’

Nevertheless, there are many Japanese origami enthusiasts doing interesting new work, and I travelled to Tsukuba, a modern university town just north of Tokyo, to meet one of them. Kazuo Haga is a retired entomologist, whose professional expertise is in the embryonic development of insect eggs. His tiny office was stacked with books and display cases of butterflies. Haga, who is aged 74, was wearing large glasses with a thin black rim that framed his face geometrically. I noticed immediately that he is a very shy man, soft and modest – and was rather nervous of being interviewed.

But Haga’s timidity is only social. In origami he is a rebel. Choosing to stay out of the origami mainstream, he has never felt constrained by any conventions. For example, according to the rules of traditional Japanese origami, there are only two ways to make the first fold. Both are folding it in half – either folding along a diagonal, bringing two opposing corners together, or along the midline, bringing adjacent corners together. These are known as the ‘primary creases’ – the diagonals and the midlines of the square.

Haga decided to be different. What if he folded a corner on to the midpoint of a side? Ker-azee! He did this for the first time in 1978. This simple fold had the effect of opening the curtains on to a sublime new world. Haga had created three right-angled triangles. Yet these were not any old right-angled triangles. All three were Eygptian, the most histct eggsand iconic triangle of them all.

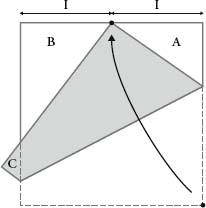
Haga’s theorem: A, B and C are Egyptian.

Feeling the thrill of discovery, but having no one to share it with, he sent a letter about the fold to Professor Koji Fushimi, a theoretical physicist known to have an interest in origami. ‘I never got a reply,’ said Haga, ‘but then all of a sudden he wrote an article in a magazine called Mathematics Seminar referring to Haga’s Theorem. That was the substitute for his reply.’ Since then Haga has given his name to two other origami ‘theorems’, although he says he has another 50. He tells me this not as evidence of arrogance but as a measure of how the area is so rich and untapped.

In Haga’s Theorem a corner is folded on to the midpoint of a side. Haga wondered if anything interesting might be revealed if he folded a corner on to a random point on the side. Deciding to demonstrate this to me, he took a blue piece of square origami paper and marked an arbitrary point on one of the sides with a red pen. He folded one of the opposite corners on to this mark, leaving a crease, and then unfolded it. He then folded the other opposite corner on to the mark to make a second crease, leaving the square now with two separate intersecting lines.

Haga’s other theorem.

Haga showed me that the intersection of the two folds was always on the middle line of the paper, and that the distance from the arbitrary point to the intersection was always equal to the distance from the intersection to the opposite corners. I found Haga’s folds totally mesmerizing. The point had been chosen randomly, and was off-centre. Yet the process of folding behaved like a self-correcting mechanism.

Haga wanted to show me a final pattern. The name he chose for this discovery sounded like a haiku: an arbitrarily made ‘mother line’ bears eleven wonder babies.

Mother line showing seven of her eleven wonder babies.

Again, this is very simple to carry out, and reveals a beautiful geometric order. Every intersection is on the primary creases, as F shows. (The diagram shows the seven intersections that are inside the original square; the other four are on extensions of the folds.) The first fold was random, yet all the folds meet with perfect concision and regularity on diagonals and midlines.

It struck me that if any man can be said to embody the soul of Pythagoras in the modern world, it is surely Kazuo Haga. Both men share a passion for mathematical discovery based on a wonder for the simple harmonies of geometry. The experience seemed to have touched Haga spiritually, the same way it did Pythagoras two millennia ago. ‘Most of the Japanese are trying to create new shapes in mi,’ said Haga. ‘My aim was to escape from the idea that you have to create something physical, and instead discover mathematical phenomena. That is why I find it so interesting. You find that in the very, very simple world you can still discover fascinating things.’