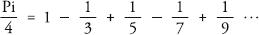In the early nineteenth century, news of boy wonder George Parker Bidder, the son of a Devonshire stonemason, reached the ears of Queen Charlotte. She had a question for him:

‘From the Land’s-end, Cornwall, to Farret’s-head, in Scotland, is found by measurement to be 838 miles; how long would a snail be creeping that distance, at the rate of 8 feet per day?’

The exchange and the answer – 553,080 days – is mentioned in a popular book of the time, A short Account of George Bidder, the celebrated Mental Calculator: with a Variety of the most difficult Questions, Proposed to him at the principal Towns in the Kingdom, and his surprising rapid Answers! The pages list the child’s greatest calculations, including such classics as ‘What is the square root of 119,550,669,121?’ (345,761, answered in half a minute) and ‘How many pounds weight of sugar are there in 232 hogsheads, each weighing 12cwt. 1qr. 22lbs?’ (323,408lbs, also answered in half a minute.)

Arabic numerals made doing sums easier for everyone, but an unexpected consequence was the discovery that certain people were blessed with truly astonishing arithmetical skills. Often, these prodigies excelled in no other way than their facility with numbers. One of the earliest-known examples was a Derbyshire farmhand, Jedediah Buxton, who amazed locals with his abilities in multiplication despite being barely able to read. He could, for example, calculate the value of a farthing when doubled 140 times. (The answer is 39 digits long, with 2 shillings 8 pence left over.) In 1754, curiosity about Buxton’s talent led to him being invited to visit London, where he was examined by members of the Royal Society. He seems to have had some of the symptoms of high-functioning autism, for when he was taken to see Shakespeare’s Richard III he was left nonplussed by the experience, although he notified his hosts that the actors had taken 5202 steps and spoken 14,445 words.

In the nineteenth century ‘lightning calculators’ were international stage stars. Some showed aptitude at an extraordinarily young age. Zerah Colburn, from Vermont, was five when he gave his first public demonstration and eight when he sailed to England with dreams of big-time success. (Colburn was born with hexadactyly, but it is not known if his extra fingers gave him an advantage when learning to count.) A contemporary of Colburn’s was the Devonshire lad George Parker Bidder. The two prodigies crossed paths in 1818, when Colburn was 14 and Bidder 12, and the encounter, in a London pub, inevitably led to a maths duel.

Colburn was asked how long it would take a balloon to circumnavigate the globe if the balloon were travelling at 3878 feet per minute and the world were 24,912 miles around. It was a suitably international question for the unofficial title of smartest alec on Earth. But after deliberating for nine minutes, Colburn failed to give an answer. A London newspaper gushed that his opponent, on the other hand, took only two minutes before giving the correct reply, ‘23 days, 13 hours and 18 minutes, [which] was received with marks of great applause. Many other questions were proposed to the American boy, all of which he refused answering; while young Bidder replied to all.’ In his charming autobiography, A memoir of Zerah Colburn, written by himself, the American gives a different version of the contest. ‘[Bidder] displayed great strength and power of mind in the higher branches of arithmetic,’ he said, before adding dismissively, ‘but he was unable to extract the roots, and find the factors of numbers.’ The mpionship was left undecided. Edinburgh University subsequently offered to take over Bidder’s education. He went on to become an important engineer, at first in railroads and eventually supervising construction of London’s Victoria Docks. Colburn, on the other hand, returned to America, became a preacher and died aged 35.

The ability to calculate rapidly has no great correlation with mathematical insight or creativity. Only a few great mathematicians have demonstrated lightning-calculator skills, and many mathematicians have surprisingly poor arithmetic. Alexander Craig Aitken was a well-known lightning calculator in the first half of the twentieth century, unusual in that he was also a professor of mathematics at Edinburgh University. In 1954 Aitken gave a lecture to the Society of Engineers in London, in which he explained some of the methods in his repertoire, such as algebraic shortcuts and – crucially – the importance of memory. To prove his point he rattled off the decimal expansion for , which repeats only after 96 digits.

Aitken ended his talk with the rueful comment that when he acquired his first desk calculator his abilities began to deteriorate. ‘Mental calculators may, like the Tasmanian or the Moriori, be doomed to extinction,’ he predicted. ‘Therefore…you may be able to feel an almost anthropological interest in surveying a curious specimen, and some of my auditors here may be able to say in the year 2000 ce, “Yes, I knew one such.”’

This was one calculation, however, that Aitken got wrong.

 

‘Neurons! On the ready! Go!’

With an impatient snap and swoosh, the contestants in the multiplication round at the Mental Calculation World Cup turned over their papers. The room at Leipzig University was silent as the 17 men and two women contemplated the first question: 29,513,736× 92,842,033.

Arithmetic is back in vogue. Thirty years after the first cheap electronic calculators precipitated a widespread demise in mental calculation skills, a backlash is under way. Newspapers offer up daily maths brainteasers, popular computer games with arithmetic puzzles sharpen our minds and – at the high end – lightning calculators compete in regular international tournaments. The Mental Calculation World Cup was founded in 2004 by German computer scientist Ralf Laue, and takes place every two years. It was the inevitable culmination of Laue’s two hobbies: mental arithmetic and collecting unusual records (such as the Most Grapes Thrown over a Distance of 15ft and Caught in the Mouth in One Minute, which is 55 of them). The internet helped, enabling him to meet kindred spirits – mental arithmeticians are not, in general, extroverts. The global community of human calculators, or ‘mathletes’, was well represented in Leipzig, with contestants from countries as diverse as Peru, Iran, Algeria and Australia.

How do you measure calculating skills? Laue adopted the categories already chosen by Guinness World Records – the multiplication of two eight-digit numbers, the addition of ten ten-digit numbers, extracting the square root of six-figure numbers to eight significant figures, and finding the day of the week of any date between 1600 and 2100. The latter is known as a calendar calculation, and is a flashback to the golden age of lightning calculation, when performers would ask a member of the audience their birth date and then instantly name the day of the week it fell on.

Regulation, and a spirit of competitiveness, have come at the expense of theatrics. The youngest contestant at the World Cup, an 11-year-old boy from India, performed the ‘air abacus’ – his hands were jerking wildly around rearranging imaginary beads, while all the others were quiet and still, occasionally jotting down their answers. (The rules say that only the final answer can be written down.) After 8 minutes and 25 seconds, Alberto Coto of Spain stuck his hand up like an excited schoolboy. The 38-year-old had completed ten multiplications of two eight-digit numbers in that time, smashing the world record. It was evidently an awesome accomplishment, yet watching him was as compelling as invigilating an exam.

Conspicuously absent from proceedings in Leipzig, however, was perhaps the world’s most famous mathlete, the French student Alexis Lemaire, who prefers another yardstick to measure computational power. In 2007 Lemaire, aged 27, made international headlines when, at the Science Museum in London, he took just 70.2 seconds to calculate the thirteenth root of:

Lemaire’s achievement was undoubtedly the more spectacular. The number has 200 digits, which can barely be pronounced in 70.2 seconds. But did his feat mean that, as he claims, he is the greatest lightning calculator of all time? This is a matter of deep controversy in the calculation milieu, mirroring the battle almost 200 years ago between Zerah Colburn and George Bidder, both exceptional at their own type of sum.

The term ‘thirteenth root of a’ refers to the number that when multiplied by itself 13 times equals a. Only a fixed amount of numbers when multiplied by themselves 13 times equal a 200-digit number. (It is a large fixed amount. The answer is limited to about 400 trillion possibilities, all 16 digits long and beginning with 2.) Because 13 is prime and considered unlucky, Lemaire’s calculation was vested with an extra aura of mystery. In fact, 13 brings with it some advantages. For instance when 2 is multiplied by itself 13 times, the answer ends in 2. When 3 is multiplied by itself 13 times the answer ends in 3. The same is true for 4, 5, 6, 7, 8 and 9. In other words, the last digit of the thirteenth root of a number is the same as the last digit of the original number. We get this number for free, without having to do any calculation.

Lemaire has worked out algorithms, which he has not divulged, to calculate the other 14 digits in the final answer. Purists, possibly unfairly, say that his skill is less a feat of calculation and more one of memorizing huge strings of numbers. And they point out that Lemaire cannot find the thirteenth root of any 200-digit number given to him. At the Science Museum in London he was presented with several hundred numbers and allowed to select the one that he would do the calculation for.

Still, Lemaire’s performance was more in keeping with the tradition of the stage calculators of old. Audiences want to feel the ‘wow’, rather than understand the process. By contrast, at the Mental Calculation World Cup, Coto had no choice about the problem to be solved and used no hidden techniques when he multiplied 29,513,736×92,842,033. He simply used his 1-to 9-times tables. The fastest way to multiply eight digits by eight digits is using the Vedic sutra Vertically and Cross-Wise, which breaks the sum into 64 multiplications of single-digit figures. He managed to get the right answer in an average of less than 51 seconds. Knowing what he was doing made it less dazzling, even though it was obviously still a formidable feat.

As I talked with competitors in Leipzig, I discovered that many of them had fallen in love with speed arithmetic thanks to Wim Klein, a Dutch lightning calculator who was a celebrity in the 1970s. Klein was already a veteran of circuses and music halls when, in 1958, he was given a job by Europe’s top physics institute – the European Organization for Nuclear Research (CERN) in Geneva, providing calculations for the physicists. He was probably the last human calculator to have been employed as one. As computers developed, his skills became redundant, and in retirement he returned to showbiz, appearing frequently on TV. (Klein, in fact, was one of the first to promote thirteenth-root calculations.)

A century before Klein another human calculator, Johann Zacharias Dase, was also employed by the scientific establishment to do their sums for them. Dase was born in Hamburg and started performing as a lightning calculator in his teens, when he was taken under the wing of two eminent mathematicians. In the days before electronic or mechanical calculators, scientists relied on logarithm tables to do complicated multiplications and divisions. As I will explain in more detail later, every number has its own logarithm, which can be calculated using a laborious procedure of adding fractions. Dase calculated the natural logarithms of the first 1,005,000 numbers, each to seven decimal places. It took him three years, and he said he enjoyed the task. Then, on the recommendation of the mathematician Carl Friedrich Gauss, Dase embarked on another enormous project: compiling a table of factors of all the numbers between 7,000,000 and 10,000,000. This means he looked at every number in the range and calculated its factors, which are the whole numbers that divide that number. For example, 7,877,433 has only two factors: 3 and 2,625,811. When Dase died, aged 37, he had completed a substantial part of it.

Yet it was another calculation for which Dase is best remembered. When still a teenager he calculated pi to 200 places, a record for the time.

 

Circles are everywhere in the natural world – you see them in the full moon, in the eyes of humans and animals and in the cross-section of an egg. Tie a dog to a post and the path it patrols when the lead is taut is a circle. The circle is the simplest two-dimensional geometrical shape. An Egyptian farmer counting how much of a crop to plant in a round field, or a Roman mechanic measuring the length of wood for a wheel would have needed to make calculations involving circles.

The ancient civilizations realized that the ratio of a circle’s circumference to its diameter was always the same no matter how big or small you made the circle. (The circumference is the distance around a circle, and the diameter is the distance across it.) The ratio is known as pi, or p, and it works out as just over three. So, if you take the diameter of a circle and curve it around the circumference, you will find that it fits just over three times.

Even though pi is a simple ratio between the basic properties of a circle, the task of finding its exact value has proved to be far from simple. This elusiveness has made pi an object of fascination for thousands of years. It is the only number that is both the name of a song by Kate Bush and a fragrance by Givenchy, whose PR department sent me the following text:

 

– PI

BEYOND INFINITY

 

Four thousand years have passed and the mystery remains.

Although every schoolchild studies, the familiar symbol still manages to hide an abyss of great complexity.

 

Why choose to symbolise the eternal masculine?

 

It’s a matter of signs and directions. If is the story of the long struggle to achieve the unattainable, it is also a portrait of the fabled conqueror in search of knowledge.

 

Pi speaks of men, of all men, of their scientific genius, their taste for adventure, their willingness to act, and of their passions to the extreme.

 

The earliest approximations for pi came from the Babylonians, who used a value of 3 , and the Egyptians, who used 4(, which translate, respectively, into decimals as 3.125 and 3.160. A line in the Bible reveals a situation in which pi is taken as 3: ‘Also he made a molten sea of ten cubits from brim to brim, round in compass, and five cubits the height thereof; and a line of thirty cubits did compass it round about’ (I Kings 7:23).

If the shape of the sea is a circle with a circumference of 30 cubits and a diameter of 10, then pi is , or 3. Many excuses have been given for the Bible’s inaccurate value, such as the claim that the sea was in a circular vessel with a thick rim. In this case the quoted 10-cubit diameter covers the sea and the rim (making the true diameter of the sea a little less than 10 cubits), while the circumference of the sea is taken as the inside of the rim. A mystical explanation is much more enticing: due to the peculiarities of Hebrew pronunciation and spelling, the word ‘line’, or qwh, is pronounced qw. Totting up the numerological values of the letters gives 111 for qwh and 106 for qw. Multiplying three by gives 3.1415, which is pi correct to five significant figures.

The first genius whose extreme passion for discovery about pi does justice to the aspirations of Givenchy’s aftershave is equally the man who took the most famous bath in the history of science. Archimedes slipped into the tub and noticed that the volume of water he displaced was equal to the volume of his own body under the water. He instantly realized that he could therefore find the volume of any object by submersing it, in particular the crown of the King of Syracuse, and so would be able to ascertain if that piece of royal bling was made of pure gold or not by working out its density. (It wasn’t.) As a result, he ran naked into the streets shouting ‘Eureka! [I have found it!]’, thus displaying – for the citizens of Syracuse, at least – the eternal masculine. Archimedes loved to grapple with problems in the real world, unlike Euclid, who dealt uniquely in abstractions. His many inventions were said to have included a giant catapult and a system of huge mirrors that reflected the sun’s rays with such intensity that they set Roman ships ablaze during the Siege of Syracuse. He was also the first person to come up with an apparatus to capture pi.

To do so he first drew a circle, and then he constructed two hexagons – one that he fitted inside the circle, and one that he put outside it, as in the diagrams below. This already tells us that pi must be somewhere between 3 and 3.46, which is determined by calculating the perimeters of the hexagons. If we let the diameter of the circle be 1, then the perimeter of the inner hexagon is 3, which is less than the circumference of the circle, which is pi, which is less than the perimeter of the outer one, which is 3 , or 3.46 to two decimal places. (The way that Archimedes calculated this value was by using a method that was essentially a fiddly precursor to trigonometry, and which is too complicated to go into here.)

So, 3 < pi < 3.46.

Now if you were to repeat the calculation using two regular polygons with more than six sides, you would get a narrower bound for pi. This is because the more sides that the polygons have, the closer their perimeters are to the circumference, as we can see in the diagram above that uses a 12-sided polygon. The polygons act like walls closing in on pi, squeezing it from above and from below, between narrower and narrower limits. Archimedes started with a hexagon and eventually constructed polygons of 96 sides, allowing him to calculate pi as follows: 3 < pi < 3

This translates into 3.14084 < pi < 3.14289, an accuracy of two decimal places.

But pi hunters weren’t about to stop there. In order to get closer to the number’s true value, all that was required was to create polygons with more sides. Liu Hui, in third-century China, employed a similar method, using the area of a polygon of 3072 sides to pin pi to five decimal places: 3.14159. Two centuries later Tsu ChungChih and his son Tsu Keng-Chih went one digit further, to 3.141592, with a polygon of 12,288 sides.

The Greeks and the Chinese were hampered by cumbersome notation. When mathematicians were eventually able to use Arabic numerals, the record tumbled. In 1596 the Dutch fencing master Ludolph van Ceulen used a souped-up polygon of 60 × 2²⁹ sides to find pi to 20 decimal places. The pamphlet on which he printed his result ended with the words: ‘whoever wants to, can come closer’, and no one felt the urge as strongly as he did. He went on to calculate pi to 32 and then 35 decimal places – which were engraved on his tombstone. In Germany, die Ludolphsche Zahl, Ludolph’s number, is still understood as a term for pi.

 

For 2000 years the only way to pinpoint pi with accuracy was by using polygons. But, in the seventeenth century, Gottfried Leibniz and John Gregory ushered in a new age of pi appreciation with the formula:

In other words, a quarter of pi is equal to one minus a third plus a fifth minus a seventh plus a ninth and so on, alternating the addition and subtraction of unit fractions of the odd numbers as they head to infinity. Before this point scientists were only aware of the scatter-gun randomness of pi’s decimal expansion. Yet here was one of the most elegant and uncomplicated equations in maths. Pi, the poster boy of disorder, it turned out, had some kind of order in his DNA.

Leibniz had devised the formula using ‘the calculus’, a powerful type of mathematics he had discovered, in which a new understanding of infinitesimal amounts was used to calculate areas, curves and gradients. Isaac Newton had also come up with calculus, independently, and the men spent a good deal of time bickering about who had got there first. (For years, Newton was considered to have won the argument, based on the dates of his unpublished manuscripts, but it now appears that a version of calculus was actually first invented in the fourteenth century by the Indian mathematician Madhava.)

The formula that Leibniz found for pi is what is known as an infinite series, a sum that goes on and on for ever, and it provides a way to calculate pi. First, we need to multiply both sides of the formula by 4 to get:

Starting with the first term and adding successive terms produces the following progression (converted into decimals):

The total gets closer and closer to pi in smaller and smaller leaps. Yet this method requires more than 300 terms to get an answer for pi accurate to two decimal places, so it was impracticable for those wanting to use it to find more digits in the decimal expansion.

Eventually, calculus provided other infinite series for pi that were less pretty but more effective for number-crunching. In 1705 the astronomer Abraham Sharp used one to calculate pi to 72 decimal places, smashing van Ceulen’s century-old record of 35. While this was quite an achievement, it was also a useless one. There is no practical reason to know pi to 72 digits, or to 35 digits for that matter. Four decimal places is enough for the engineers of precision instruments. Ten decimal places is sufficient to calculate the circumference of the Earth to within a fraction of a centimetre. With 39 decimal places, it is possible to compute the circumference of a circle surrounding the known universe to within an accuracy of a radius of a hydrogen atom. But practicality wasn’t the point. Application was not a concern to the pi men of the Enlightenment; digit-hunting was an end in itself, a romantic challenge. A year after Sharp’s effort, John Machin reached 100 digits and in 1717 the Frenchman Thomas de Lagny added a further 27. By the turn of the century, the Slovenian Jurij Vega was in the lead with 140.

Zacharias Dase, the German lightning calculator, pushed the record for pi to 200 decimal places in 1844 in an intense two-month burst. Dase used the following series, which looks more convoluted than the pi formula above but is in fact far more user-friendly. This is because, first, it bears down on pi at a respectable rate. An accuracy of two decimal places is reached after the first nine terms. Second, the , and that reappear every third term are very convenient to manipulate. If is rewritten as and as ××, all the multiplications involving those terms can be reduced to combinations of doubling and halving. Dase would have written out a reference table of doubles to help him with his calculations, starting 2, 4, 8, 16, 32, and carried on for as far as he needed – which, since he was calculating pi to 200 places, would be when the final double is 200 digits long. This happens after 667 successive doublings.

Dase used this series:

 

Dase barely had time to rest on his laurels before the Brits decided to covet his achievement, and within a decade William Rutherford had calculated pi to 440 places. He encouraged his protégé William Shanks, an amateur mathematician who ran a boarding school in County Durham, to go even further. In 1853 he reached 607 digits, and by 1874 he was at 707. His record held for 70 years until D.F. Ferguson, of the Royal Naval College in Chester, found a mistake in Shanks’s calculation. He had made an error at the 527th place so all the subsequent numbers were wrong. Ferguson spent the last year of the Second World War calculating pi longhand. One can only assume that he thought the war was already won. By May 1945 he had 530 places, and by July 1946 he reached 620, and no one has ever calculated further using only paper and pen.

Ferguson was the last of the manual digit-hunters and the first of the mechanical. Using a desk calculator he added almost another 200 places in just over a year, so in September 1947 pi was known to 808 decimal places. Computers then changed the race. The first of them to battle pi was the Electronic Numerical Integrator and Computer, or ENIAC, which was built in the final years of the Second World War at the US Army’s Ballistic Research Laboratory in Maryland. It was the size of a small house. In September 1949 the ENIAC took 70 hours to calculate pi to 2037 digits – smashing the record by more than a thousand decimal places.

 

As more and more digits were found in pi, one thing seemed pretty clear: the numbers obeyed no obvious pattern. Yet it was only in 1767 that mathematicians were able to prove that the higgledy-piggledy sequence of digits would never repeat itself. The discovery followed from considering what type of number pi might be.

The most familiar type of number is the natural numbers. They are the counting numbers starting at one:

The natural numbers, however, are limited in scope because they expand in only one direction. More ul are the integers, which are the natural numbers together with zero and the negatives of the natural numbers:

The integers cover every positive or negative whole number from minus infinity to plus infinity. If there were a hotel with an unlimited amount of floors and an unlimited amount of lower and lower basements, the buttons in the elevator would be the integers.

Another basic type of number is the fraction, which are the numbers written when a and b are integers but b is not 0. The top number in a fraction is the numerator and the bottom number is the denominator. If we have several fractions, the lowest common denominator is the lowest number that can be divided by all the denominators without leaving a remainder. So, if we have and , the lowest common denominator is 10, since both 2 and 10 divide into 10. What about the lowest common denominator of ,, and ? In other words, what is the smallest number that 3, 4, 9 and 13 divide into? The answer is surprisingly big: 468! I mention this to make a semantic rather than a mathematical point. The phrase ‘lowest common denominator’ is often used to describe something basic or unsophisticated. It sounds evocative, but misrepresents the arithmetic. Lowest common denominators can often be big and unconventional: 468 is quite an impressive number! A more arithmetically meaningful phrase for something mainstream and cheap is highest common factor – which is the largest number that can be divided into every one of a group of numbers. The highest common factor of 3, 4, 9 and 13, for example, is 1, and you can’t get much lower or more unsophisticated than that.

Since fractions are equivalent to ratios between integers, they are also called rational numbers, and there is an infinite amount of them. In fact, there is an infinite number of rational numbers between 0 and 1. For example, let’s take every fraction where the numerator is 1 and the denominator is a natural number bigger than or equal to 2. This is the set composed of:

We can go further and prove that there is an infinite number of rational numbers between any two rational numbers. Let c and d be any two rational numbers, with c less than d. The point halfway between c and d is a rational number: it is . Call this point e. We can now find a point halfway between c and e. It is . It is rational and also between c and d. We can carry on ad infinitum, always splitting the distance between c and d into smaller and smaller parts. No matter how tiny the distance between c and d is in the first place, there will always n infinite amount of rational numbers in between them.

Since we can always find an infinite number of rational numbers between any two rational numbers, it might be thought that the rational numbers cover every number. Certainly, this is what Pythagoras had hoped. His metaphysics was based on the belief that the world was made up of numbers and the harmonic proportions between them. The existence of a number that could not be described as a ratio diminished his position, at the very least, if it did not contradict it outright. Yet unfortunately for Pythagoras, there are numbers that cannot be expressed in terms of fractions, and – rather embarrassingly for him – it is his own theorem that leads us to one. If you have a square where each side has length 1, then the length of the diagonal is the square root of two, which cannot be written as a fraction. (I have included a proof as an appendix.)

Numbers that cannot be written as fractions are called irrational. According to legend, their existence was first proved by the Pythagorean disciple Hippasus, which did not endear him to the Brotherhood; he was declared a heretic and was drowned at sea.

When a rational number is written out as a decimal fraction, either it has a finite amount of digits, in the way that can be written 0.5, or the expansion will end up repeating itself, just as is 0.3333…where the 3s go on for ever. Sometimes the recurring loop is more than one digit, as is the case of , which is 0.090909…where the digits 09 repeat for ever, or , which is 0.0526315789473684210…where 052631578947368421 repeats for ever. By contrast, and this is the crucial point, when a number is irrational its decimal expansion never repeats.

In 1767 the Swiss mathematician Johann Heinrich Lambert proved that pi was indeed irrational. The early pi-men may have hoped after the initial chaos of 3.14159…that the noise would calm and a pattern ensue. Lambert’s discovery confirmed that this was impossible. Pi’s decimal expansion cavorts towards infinity in a predestined yet apparently indiscriminate way.

 

Mathematicians interested in the irrationals wanted to categorize them further. In the eighteenth century they started to speculate about a special type of irrational called transcendental numbers. These were numbers so mysterious and evasive that finite mathematics could not capture them. The square root of two,, for example, is irrational but can be described as the solution to the equation x² = 2. A transcendental number is an irrational that cannot be described by an equation with a finite amount of terms. When the concept of transcendental numbers was first mooted, no one knew if they even existed.

They did exist, although it took about a hundred years before Joseph Liouville, a French mathematician, came up with a few examples. Pi was not among them. Only after another 40 years did the German Ferdinand von Lindemann prove that pi was indeed transcendental. The number existed beyond the realm of finite algebra.

Lindemann’s discovery was a milestone for number theory. It also settled, once and for all, what was probably the most celebrated unsolved problem in mathematics: whether or not it was ple to square the circle. In order to explain how it did this, however, I need to introduce the formula that says that the area of a circle is r², where r is the radius. (The radius is the distance from the centre to the side, or half the diameter.) A visual proof of why this is true is an instance where a pie is the best metaphor for pi. Imagine you have two same-sized circular pies, a white one and a grey one, as below in A. The circumference of each pie is pi times the diameter, or pi times twice the radius, or 2pr. When sliced into equal segments the pieces can be rearranged, as in B with quarter segments, or as in C with ten segments. In both cases the length of the side remains 2pr. If we keep on slicing smaller and smaller segments, then the shape would eventually become a rectangle, as in D, with sides r and 2r. The area of the rectangle – which is the area of the two pies – is therefore 2r², so the area of one pie is r².

 

To square a circle we must construct (using just a compass and straightedge) a square that has the same area as a given circle. Now we know that a line with length r is the radius of a circle with area r², and we also know that a square with area r² must have a side length r (since (). So squaring the circle can be reduced to the challenge of constructing the length r from the length r. Or, taking r as 1 for convenience, the length from 1.

Using coordinate geometry, which I will cover later, it is possible to express the process of the construction of a line algebraically, as a finite equation. It can be shown that so long as x is the solution to a finite equation, then starting with a line of length 1 we can construct a line with length x. But if x is not the solution to a finite equation – in other words, if x is transcendental – it is impossible to construct a line with length x. Now, the fact that p is transcendental means that is also transcendental. (You’re going to have to trust me on that.) So it is impossible to construct the length . The transcendence of pi proves that the circle cannot be squared.

Lindemann’s proof of the transcendence of pi dashed what had been the dream, for thousands of years, of countless mathematicians. Perhaps the most eminent figure ever to have declared that he had squared the circle was Thomas Hobbes, the seventeenth-century English thinker whose book Leviathan founded political philosophy. Having become a keen amateur geometer in later life, Hobbes published his solution when he was 67. Even though circle-squaring was still an open question at the time, his proof was received with bemusement by the scientific community. John Wallis, professor at Oxford and the finest British mathematician before Isaac Newton, exposed Hobbes’s errors in a pamphlet, thus setting in motion one of the most entertaining – and pointless – feuds in the history of British intellectual life. Hobbes replied to Wallis’s comments with an addendum to his book entitled Six Lessons to the Professors of Mathematics. Wallis countered with Due Correction for Mr Hobbes in School Discipline for not saying his Lessons right. Hobbes followed this with Marks of the Absurd Geometry, Rural Language, Scottish Church Politics and Barbarisms of John Wallis. This led to Wallis’s Hobbiani Puncti Dispunctio! or the Undoing of Mr Hobbes’s Points. The quarrelling lasted almost a quarter of a century, until Hobbes’s death in 1679. Wallis rather enjoyed the hostilities, since it was a way of casting aspersions on Hobbes’s political and religious views, which he despised. And, of course, he was right. In many disputes truths are shared between both sides. Not in Hobbes vs Wallis. Hobbes could not square the circle because it is impossible to do so.

Proof that you cannot square the circle has not put people off trying. In 1897 the Indiana state legislature famously considered a bill containing a proof of squaring the circle by E.J. Goodwin, a country doctor, who offered it ‘as a gift to the State of Indiana’. He was, of course, misguided. Since Ferdinand von Lindemann in 1882, the phrase circle-squarer has been mathspeak for crank.

 

Pi’s enigmatic attributes were, in the eighteenth and nineteenth centuries, revealed not only to be at the heart of ancient geometrical problems but also deeply rooted in new fields of science that were not always obviously related to circles. ‘This mysterious 3.141592…which comes in at every door and window, and down every chimney,’ wrote the British mathematician Augustus De Morgan. For example, the time it takes a pendulum to swing is dependent on pi. The distribution of deaths in a population is a function of pi. If you toss a coin 2n times, the probability when n is very large of getting exactly 50 percent heads and 50 percent tails is .

The man whose name is most associated with offbeat occurrences of pi was the French polymath Georges-Louis Leclerc, the Comte de Buffon (1707–88). Of Buffon’s many colourful scientific endeavours, perhaps his most ambitious was the construction of a working version of Archimedes’ weapon of mirrors, with which he was said to have set fire to ships. Buffon’s contraption was made up of 168 flat mirrors, each six by eight inches, and it was able to ignite a wooden plank at a distance of 150 feet, a good effort, though on a different scale from setting a Roman fleet ablaze.

With regard to pi, Buffon is remembered for having devised an equation that led to a new method for calculating pi, though Buffon did not himself make the connection. Buffon arrived at his equation by studying an eighteenth-century gambling game called ‘clean tile’, in which you throw a coin on to a tiled surface and bet on whether it will touch the cracks between tiles or rest cleanly. Buffon came up with the following alternative scenario: imagine that a floor is marked with parallel lines spaced evenly apart and that a needle is thrown on it. He then correctly calculated that if the length of the needle is l and the distance between lines is d, then the following equation holds:

 

Probability of the needle touching the line =

A few years after Buffon died, Pierre Simon Laplace realized that this equation could be used to estimate a value for pi. If you throw lots and lots of needles on the floor, then the ratio of the number of times that the needle hits the line to the total number of throws will be approximately equal to the mathematical probability of the needle touching the line. In other words, after many throws

 

 

or:

 

 

(The symbol means ‘is approximately equal to’.)

 

Even though Laplace was the first to write about how pi could be estimated this way, his work followed from Buffon’s equation, so Buffon is the person remembered for it. His achievement put him in esteemed company as a member of the club of mathematicians, including Archimedes and Leibniz, who each found a new way to calculate pi.

 

The more throws of the needle that are taken, the better the approximation, and aiming needles at boards has become a standard diversion for mathematicians unable to think of more creative ways to pass the time. You need, however, to keep on going a fair while before any interesting result is achieved. An early adopter is said to have been a certain Captain Fox in the American Civil War, who, while recovering from battle wounds, threw a piece of wire eleven hundred times on a board of parallel lines and managed to derive pi to 2 decimal places.

Pi’s mathematical properties have made it a celebrity among numbers, and also a more general cultural icon. Because pi’s digits never repeat, they are perfect for feats of memorization. If remembering numbers is your thing, the ne plus ultra of digits is the digits in pi. This has been a pastime since at least 1838, when The Scotsman reported that a 12-year-old Dutch boy recited all the 155 digits that were known at the time to an audience of scientists and royals. Akira Haraguchi, a 60-year-old retired engineer, holds the current world record. In 2006 he was filmed in a public hall near Tokyo reciting pi to 100,000 decimal places. The performance took him 16 hours and 28 minutes, including five-minute breaks every two hours to eat rice balls. He explained to a journalist that pi symbolized life since its digits never repeated and followed no pattern. Memorizing pi, he added, was ‘the religion of the universe’.

Pi memorization gets a little dull, but pi memorization while juggling, now there’s a competitive sport! The record is held by Mats Bergsten, an actuary in Sweden in his late fifties, who has recited 9778 digits while juggling with three balls. He told me, however, that he is proudest of his achievements in the ‘erest test’, in which the first 10,000 digits of pi’s expansion are divided into 2000 groups of five, beginning with 14159. In the test 50 groups are randomly read out, and the contestant has to say from memory which five numbers precede and succeed each of them. Mats Bergsten is one of only four people in the world who can do this with no errors, and his time, 17min 39secs, is the fastest. It is much more mentally straining, he told me, to recall 10,000 digits randomly than merely remembering them in order.

When Akira Haraguchi recited 100,000 digits of pi by heart, he used a mnemonic technique, assigning syllables to each number from 0 to 9 and then translating pi’s decimals into words, which in turn formed sentences. The first fifteen digits sounded like: ‘the wife and children have gone abroad; the husband is not scared.’ Using words to remember the digits in pi this way is used by schoolchildren in cultures all over the world, but usually this is done not by assigning syllables, but by creating a phrase in which the number of letters in each word represents each consecutive digit in the decimal expansion of pi. A well-known English one is credited to the astrophysicist Sir James Jeans: How I need a drink, alcoholic in nature, after the heavy lectures involving quantum mechanics. All of thy geometry, Herr Planck, is fairly hard. ‘How’ has 3 letters, ‘I’ has 1, ‘need’ has 4, and so on.

Among numbers, only pi has inspired this type of fandom. No one wants to memorize the square root of two, which is just as challenging. Pi is also the only number to have inspired its own literary subgenre. Constrained writing is a technique in which some condition is adopted that imposes a pattern or forbids certain things in the text. Entire poems – or ‘piems’ – have been written under the constraint that the number of letters per word is determined by pi, usually with the convention that a 0 in the expansion requires a ten-letter word. The most ambitious piem is the Cadaeic Cadenza by Mike Keith, which follows pi for 3835 digits. It begins as a pastiche of Edgar Allan Poe:

Keith says that writing with a difficult constraint is an exercise both in discipline and discovery. Since the digits in pi are random, the constraint is, he said, ‘like bringing order out of chaos’. When I asked him ‘Why pi?’ he replied that pi was ‘a metaphor for all things infinite, or inscrutable, or unpredictable, or full of endless wonder’.

 

Pi has gone by this name only since 1706, when the Welshman William Jones introduced the symbol p in his book, the snappily titled A New Introduction to the Mathematics, for the Use of some Friends who have neither Leisure, Convenience, nor, perhaps, Patience, to search into so many different Authors, and turn over so many tedious Volumes, as is unavoidably required to make but tolerable progress in the Mathematics. The Greek letter, which was probably an abbreviation for the word periphery, did not immediately catch on, howeve, becoming standard notation for pi only 30 years later when Leonhard Euler adopted it.

Euler was the most prolific mathematician of all time (he published 886 books), and he is possibly the one who contributed most to an understanding of pi. It was his improved formulae for pi that enabled the eighteenth-and nineteenth-century digit-hunters to peel back more and more decimal places. In the beginning of the twentieth century the Indian mathematician Srinivasa Ramanujan devised many more Euler-style infinite series for pi.

Ramanujan was a largely self-taught mathematician who worked as a clerk in Madras before writing a letter to Cambridge university professor G.H. Hardy. Hardy was flabbergasted to see that Ramanujan had rediscovered results that had taken centuries to achieve, and invited him to England, where the men collaborated before Ramanujan died aged 32. His work showed an extraordinary intuition about the properties of numbers, including pi, and his most famous formula is the following:

The symbol indicates a series of values all added up, starting with the value when n equals zero, added to the value when n equals one, and so on to infinity. Even without understanding the notation, however, one can appreciate the drama of such an equation. The Ramanujan formula races towards pi with remarkable speed. From the very start, when n is 0 the formula has one term and gives a value of pi accurate to six decimal places. For each increase in the value of n, the formula adds roughly eight new digits to pi. It is an industrial-strength pi-making machine.

Inspired by Ramanujan, in the 1980s the Ukrainian-born mathematicians Gregory and David Chudnovsky devised an even more ferocious formula. Each new term adds roughly 15 digits.

The first time I saw the Chudnovsky formula I was standing on it. Gregory and David are brothers and they share an office at the Polytechnic University in Brooklyn. It consists of an open-plan space with a sofa in the corner, a couple of chairs and a blue floor decorated with dozens of formulae for pi. ‘We wanted to put something on the floor and what else can you put on the floor other than stuff which relates to mathematics?’ explained Gregory.

In fact, the pi floor pattern was their second choice. The original plan was to lay down a giant reproduction of Melencolia I by Albrecht Dürer (reproduced on chapter 6). The sixteenth-century woodcut is beloved of mathematicians since it is full of playful references to numbers, geometry and perspective.

‘One night, when there was nothing on the surface, we printed 2000 or more pages of [Melencolia I] and we laid it on the floor,’ said David. ‘But if you walked around it, you wanted to throw up! Because your point of view changes extremely abruptly.’ David began to study the floors of the cathedrals and castles of Europe in order to work out how he could decorate the office without inducing nausea in anyone walking through. ‘I discovered they are mostly laid out in a –’

‘Simple geometric style,’ interrupted Gregory.

‘Black, white, black, white squares…#8217; said David.

‘You see, if you really have a complex picture and you try to walk on it, the angle changes so abruptly that your eyes don’t like it,’ added Gregory. ‘So the only way you can do something like that is to –’

‘Hang from the ceiling!’ David shouted in my left ear, and both men lost themselves in guffaws.

Talking to the Chudnovskys was like wearing stereo headphones with an erratically alternating connection to both ears. They sat me on their sofa and sat on either side of me. Constantly interrupting each other, they finished each other’s sentences, speaking in a highly melodic English thick with Slavic tones. The brothers were born in Kiev, when it was in the Soviet Republic of Ukraine, although they have lived in the United States since the late 1970s and are American citizens. They have collaborated on so many papers and books together that they encourage you to think of them as one mathematician, not two.

For all their genetic, conversational and professional homogeneity, however, the men look very different. This is mostly because Gregory, who is 56, suffers from myasthenia gravis, an auto-immune disorder of the muscles. He is so thin and frail that he spends most of his time lying down. I never saw him get up off the sofa. Still, the energy his limbs lacked was compensated for by a brilliantly expressive face that burst into life as soon as he talked about maths. He has pointed features, large brown eyes, a white beard and wispy unkempt hair. David, who has blue eyes, is five years older, rounder of body and fuller of face. He was clean-shaven and his short hair was hidden under an olive-green baseball cap.

The Chudnovskys are arguably the mathematicians who have done the most to popularize pi in recent years. In the early 1990s they built a supercomputer in Gregory’s Manhattan apartment out of mail-order parts that, using their own formula, calculated the number to more than two billion decimal places – a record at the time.

This amazing achievement was chronicled in a New Yorker article, which in turn inspired the 1998 film Pi. The main protagonist was an unruly-haired maths genius looking for hidden patterns in stock-market data on a homemade supercomputer. I was curious to discover if the Chudnovskys had seen the film, which garnered favourable reviews and has become a reference for low-budget, black-and-white psycho-mathematical thrillers. ‘No, no, we haven’t seen it,’ said Gregory.

‘You have to realize, usually movie-makers repeat their internal state,’ added David sarcastically.

I tell them I thought they might have been flattered by the attention.

‘No, no,’ grinned Gregory.

‘Let me tell you another thing,’ David cut in. ‘Two years ago I came back from France. A couple of days before I left, there was a huge book fair. I stopped at a stand where there was a book that had a detective story on it. It was written by an engineer. It was a murder mystery, you know. A lot of dead bodies, mostly mistress in hotel, and the source that determined everything he did was pi.’

Gregory was smiling from ear to ear and said under his breath: ‘OK, I am not going to read this book, zat’s for sure.’

David carried on: ‘So I talked to the guy. He is a very eucated man.’ He paused, shrugged his shoulders and raised his pitch by an octave: ‘As I say, I bear no responsibility!’

David said that he was taken aback the first time that he saw billboards advertising the Givenchy perfume. ‘All the way down the street was pi…pi…pi…’ He was wailing now: ‘Pi…pi…pi! Do I bear any responsibility?’

Gregory glanced at me and said: ‘For some reason, the general public is fascinated with this stuff. They get kind of the wrong inference.’ There are many professional mathematicians, he said, who study pi. He added wryly: ‘Usually these people are not allowed to see the light of day.’

 

In the 1950s and 1960s advances in computer technology were reflected in the number of new digits found in pi. By the end of the 1970s the record had been broken nine times and stood at just over a million decimal places. In the 1980s, however, a combination of even faster computers and brand-new algorithms led to a frenetic new era of digit-hunting. Yasumasa Kanada, a young computer scientist at Tokyo University, was first off the block in what became a two-way pi race between Japan and the United States. In 1981 he used an NEC computer to calculate pi to 2 million digits in 137 hours. Three years later he was up to 16 million. William Gosper, a mathematician in California, then nudged into the lead with 17.5 million, before David H. Bailey, at NASA, bettered him with 29 million. In 1986 Kanada overtook them both with 33 million and broke his own record three times in the next two years to reach 201 million with a new machine, the S-820, which did the calculation in just under six hours.

Away from the digit-hunting spotlight, the Chudnovskys were also beavering away on pi. Using a new method of communication called the internet, Gregory connected the computer at his bedside to two IBM supercomputers at different sites in the US. The brothers then devised a program to calculate pi based on the new superfast pi formula they had discovered. They were allowed on to the computers only when no one else was using them, at nights and weekends.

‘It was a great thing,’ remembered Gregory nostalgically. In those days there was no computer capacity to store the numbers that the brothers were calculating. ‘They kept the pi on magnetic tape,’ he said.

‘Mini-tape. And you had to call the guy and ask…’ added David.

‘And say tape number such and such,’ continued Gregory. ‘And sometimes if somebody else is more important your tapes are dismounted in the middle of computation.’ His eyes rolled as if to throw his hands in the air.

Despite the obstacles, the Chudnovskys kept on going, pushing beyond a billion digits. Kanada then nudged ahead of them briefly, before the Chudnovskys retook the lead with 1.13 billion. David and Gregory then decided that if they were serious about calculating pi they needed their own machine.

The Chudnovskian supercomputer lived in a room in Gregory’s apartment. Made up of processors linked by cables, the whole thing cost, according to their estimates, about $70,000. It was a steal, compared to the millions of dollars that would have bought a machine of similar capacity; although it came with its own complications to their lifestyles. The computer, which they called m zero, was switched on at all times, just in case switching it off was irreversible, and keeded 25 fans in the room to keep it cool. The brothers were careful not to switch on too many lights in the apartment just in case the added demand blew the wiring.

In 1991 David and Gregory’s homemade contraption calculated pi to more than two billion places. Then they got distracted by other problems. By 1995 Kanada was ahead once again, and he reached 1.2 trillion digits in 2002, a record that lasted only until 2008, when compatriots at the University of Tsukuba revealed 2.6 trillion. In December 2009 the Frenchman Fabrice Bellard claimed a new record using the Chudnovsky formula: almost 2.7 trillion places. The calculation had taken 131 days on his desktop PC.

If you wrote a trillion digits in small type, the distance would cover from here to the sun. If you put 5000 digits on a page (which is very small type) and stacked the pages on top of each other, the pi in the sky would be 10km high. What is the point of calculating pi to such absurd lengths? One reason is very human: records exist to be broken.

But there is another, more important motivation. Finding new digits in pi is ideal for testing the processing capacity and reliability of computers. ‘I have no interest as a hobby for extending the known value of pi itself,’ Kanada once said. ‘I have a major interest for improving the performance of the computation.’ Pi calculation is now essential for quality-testing supercomputers because it is a ‘high-duty job which requires large main memory, operates huge number-crunching and gives [an] easy [way] to check [the] correct answer. Mathematical constants like the square root of two, e^* [and] gamma are some of the candidates, but pi is most effective.’

The story of pi has wonderful circularity. It is the simplest and most ancient ratio in maths, which has been reinvented as a massively important tool on the frontline of computer technology.

In fact, the Chudnovskys’ interest in pi came primarily from their desire to build supercomputers, a passion that still burns brightly. The brothers are currently designing a chip that they claim will be the fastest in the world, only 2.7cm wide but containing 160,000 smaller chips and 1.75km of wire.

On discussion of their new chip, Gregory became very high-spirited: ‘Computers double their power every 18 months, not because they are faster but because they can pack more stuff in. But there is a catch,’ he said. The mathematical challenge was how to partition the smaller pieces so that they can talk to each other in the most efficient way. His laptop showed the chip’s circuitry. ‘I’d say the problem with this chip is that it is a capitalist chip!’ he exclaimed. ‘The problem is that most of the stuff here is not doing anything. There are not too much proles here.’ He pointed at one section. ‘This is just management of the stores inside the chip,’ he lamented. ‘The majority of these guys just do warehousing and accounting. This is awful! Where is the manufacturing sector?’

 

In Carl Sagan’s bestselling book Contact, an extraterrestrial informs a woman on Earth that after a certain amount of digits the randomness in pi stops and there is a message written in 0s and 1s. This message occurs after 10²⁰ decimal places – which is the number described by 1 followed by 20 zeros. Since we currently know pi to ‘only’ 2.7 trillion places (27 followed by 11 zeros), we have a little way to goe s to check that he was making it up. Actually, we have further to go since the message is apparently written in base 11.

The idea that there is a pattern in pi is an exhilarating one. Mathematicians have been looking for signs of order in the decimal expansion of pi for as long as there have been decimal expansions. The irrationality of pi means that the numbers keep on spewing out with no repeated pattern, but this does not eliminate the possibility of patches of order – such as a message written in 0s and 1s. So far, however, no one has found anything significant. The number, does, though, have its quirks. The first 0 comes in position 32, which is much later than expected if the digits are randomly distributed. The first time a digit is repeated six times consecutively is 999999 at the 762nd decimal place. The likelihood of six 9s occurring so early if they occur randomly is less than 0.1 percent. This sequence is known as the Feynman point, since physicist Richard Feynman once remarked that he wanted to memorize pi until that point and finish by saying ‘nine, nine, nine, nine, nine, nine, and so on’. The next time pi throws up six consecutive identical digits happens in position 193,034 and they are also 9s. Is this a message from beyond, and if so what is it saying?

A number is considered normal if each of the digits 0 to 9 occurs equally often in the number’s decimal expansion. Is pi normal? Kanada looked at the first 200 billion digits of pi and found that the digits occurred with the following frequencies:

Only the digit 8 seems a little overabundant, yet the difference is statistically insignificant. It would appear that pi is normal, yet no one has been able to prove it. And neither has anyone been able to prove that such a proof is impossible. There is a chance, therefore, that pi is not normal. Maybe after 10²⁰ there really are just 0s and 1s?

A different, but related issue, is the positioning of the numbers. Are they distributed randomly? Stan Wagon analysed the first ten million digits of pi with a ‘poker test’: take five consecutive digits and consider them as if they are a poker hand.

The right column is how many times we would expect to see the poker hands if pi was normal and each decimal place had an equal chance of being occupied by any digit. The results are well within the boundaries of what we would expect. Each pattern of numbers seems to appear with the frequency it would had each decimal place been randomly generated.

There are websites that can find you the first occurrence in pi of the numbers of your birthday. The first time the sequence 0123456789 occurs is at the 17,387,594,880th place – which was discovered only when Kanada got that far in 1997.

I asked Gregory if he ever believed an order would be found in pi. ‘There is no order,’ he replied dismissively. ‘And if there would be an order, it would be weird and not right. So there is no point wasting the time.’

Instead of focusing on patterns in pi, some see its very randomness as a tremendous expression of mathematical beauty. Pi is predetermined but it seems to mimic randomness extraordinarily well.

‘It is a very good random number,’ agreed Gregory.

Shortly after the Chudnovskys started computing pi they got a call from the United States government. David squealed an impersonation of the voice at the end of the line: ‘Could you please send pi?’

Random numbers are needed in industry and commerce. For example, just say a market-research company needs to poll a representative sample of a thousand people from a population of a million. The company will use a random-number generator to select the sample group. The better the generator is at providing random numbers, the more representative the sample will be – and the poll will be more accurate. Likewise, streams of random numbers are needed to simulate unpredictable scenarios when testing computer models. The more random the numbers, the more robust the testing will be. In fact, projects can fail if the random numbers used to test them are not random enough. ‘You are only as good as your random number,’ remarked David. ‘If you use terrible random numbers, you will end up in a terrible condition,’ concluded Gregory. Of all sets of available random numbers, the decimal expansion of pi is the best.

Yet there is a philosophical paradox. Pi is self-evidently not random. Its digits may behave like random digits, but they are fixed. For example, if the digits in pi were truly random then there would be only a 10 percent chance that the first digit after the decimal point is a 1, yet we know that it is 1 with absolute certainty. Pi exhibits randomness non-randomly – which is fascinating, and weird.

Pi is a mathematical concept that has been studied for thousands of years, yet it holds many secrets. There have been no great advances in understanding its nature since transcendence was proved almost a century and a half ago.

‘We actually don’t know about most of this stuff,’ said Gregory.

I asked if there would ever be a new advance in understanding pi.

‘Of course, of course,’ said Gregory, ‘There are always advances. Mathematics moves forward.’

‘It will be more miraculous but it won’t be nice,’ David said.

 

Nineteen sixty-eight was a year of counter-cultural uprisings around the world, and Britain was not immune to such generational upheaval. In May the Treasury announced the introduction of a revolutionary new coin.

The 50p piece was designed to replace the old ten-shilling note as part of the switch from imperial to decimal currency. Yet what set the coin apart was not its denomination, but its unorthodox shape.

‘It’s no ordinary coin,’ exhorted the Daily Mirror. ‘Why, the Decimal Currency Board even go so far as to call it a “multilateral-curve heptagon”.’ Never before had a country introduced a seven-sided coin. And never before had a nation been so outraged over the aesthetics of a geometric shape. Leading the foment was retired army colonel Essex Moorcroft, of Rosset, Derbyshire, who formed the Anti-Heptagonists. ‘We take our motto from Cromwell’s heartfelt cry, “Take away this bauble”. I have founded the society because I believe our Queen is insulted by this heptagonal monstrosity,’ he said. ‘It is an ugly coin and an insult to our Sovereign, whose image it bears.’

Nonetheless, the 50p entered circulation in October 1969, and Colonel Moorcroft did not take to the barricaes. Indeed, by January 1970 The Times reported that ‘the curvaceous heptagon seems to have won for herself some affection’. Today the 50p piece is considered a distinctive and cherished part of British heritage. When a 20p piece was introduced in 1982, it too was heptagonal.

The 50p and 20p pieces are, in fact, design classics. Their seven-sided shape means that they are easily distinguished from circular coins, helping in particular the blind and partially sighted. They are also the most thought-provoking coins in circulation. The circle is not the only interesting round shape in mathematics.

 

A circle can be defined as a curve for which every point is equidistant from a fixed point, the centre. This property has many practical applications. The wheel – generally trumpeted as humanity’s first great invention – is the most obvious. An axle attached to the centre of a wheel will stay at a fixed point above the ground when the wheel rotates smoothly along a surface, which is why carts, cars and trains run smoothly without bobbing up and down.

For the transportation of very heavy loads, however, an axle might not take the weight. One alternative is to use rollers. A roller is a long tube with a circular cross-section, laid out on the ground. If a heavy object with a flat base (such as a giant cuboidal piece of stone intended for a pyramid) is put on several rollers, then it can be pushed smoothly over the rollers, with new rollers being put in front as it inches forward.

Curves of constant width include the Reuleaux triangle (left) and the multilateral-curve heptagon, better known as the 50p piece (centre).

The crucial feature of a roller is that the distance between the ground and the top of the roller is always the same. This is obviously the case with a circular cross-section, since the width of a circle (the diameter) is always the same.

Do all rollers have to have a circular cross-section? Are there any other shapes that will work? It may appear counter-intuitive, but there are, in fact, a variety of shapes that will make perfect rollers. An example is the 50p piece.

If you welded coins together to form rollers that had a 50p piece as a cross-section and then placed this book on these rollers, the book would not wobble up and down as you pushed it along. It would ride as smoothly as if on circular cylinders.

The reason this happens is because the 50p piece is a curve of constant width. Wherever you measure it around its perimeter, the 50p has the same breadth. So, when a 50p rolls along the floor, the distance from the floor to the top of the coin is always equal. A book lying atop a set of 50p rollers therefore stays at the same height.

Surprisingly, there are many, many curves of constant width. The simplest is the Reuleaux triangle. It is constructed from an equilateral triangle by putting the point of a compass at each vertex and drawing the arc that goes between the other two vertices. In the diagram above, put the compass at A and move the pencil from B to C, and then repeat with the other vertices. The multilateral-curve heptagon is constructed the same way. Curves of constant width do not need to be symmetrical. It is possible to construct them from any number of lines crossing, as shown above right. The sections of perimeter are always arcs of a circle centred in the opposing vertex.

The curvilinear triangle owes its name to Franz Reuleaux, a German engineer who first wrote about its applications in his 1876 book Kinematics of Machinery. This was read many years later by H.G. Conway, a former president of the Institution of Mechanical Engineers, who sat on the British Treasury’s Decimal Currency Board. Conway suggested a non-circular curve of constant breadth for the 50p piece since this property made it suitable for use in coin-operated machines. Machines distinguish coins by measuring diameter, and the 50p piece has the same width whichever position it is in. (A square coin, even with rounded sides, can never have constant width, which is why there are no four-sided coins.) Seven sides were chosen since it was considered the most aesthetically pleasing.

While the Reuleaux triangle reinvented the roller, it didn’t reinvent the wheel. Wheels cannot be made of Reuleaux triangles because non-circular curves of constant width do not have a ‘centre’ – a fixed point that is equidistant from every point on the perimeter. If you put an axle on a Reuleaux triangle and rolled it, the height of the shape would stay the same but the axle would judder around.

One useful property of a Reuleaux triangle is that it can be rotated inside a square so that it touches all four sides of the square at all times. This property was exploited by Harry James Watts, an English engineer living in Pennsylvania, in 1914, when he designed one of the most bizarre tools in existence: a drill that can drill square holes. (The corners are rounded, rather than sharp, so, strictly speaking, the hole is a modified square.)

The cross-section of Watts’s invention is simply a Reuleaux triangle, with three portions removed to make a cutting edge. It comes with a special chuck to compensate for the wobble of the drill bit’s centre as it rotates. The Watts square-hole drill is still used today.

Reuleaux triangle rotating in square.

Cross-section of Watts’s square drill.