Maki Kaji runs a Japanese magazine that specializes in number puzzles. Kaji considers himself an entertainer who uses numbers as the tools of his trade. ‘I feel more like a film or theatre director than a mathematician,’ he explained. I met Kaji at his office in Tokyo. He was neither geeky nor formal, two characteristics one might expect to find in a numbers guy-turned-successful businessman. Kaji was wearing a black T-shirt under a trendy beige cardigan, and a pair of John Lennon glasses. Aged 57, he has a trim white goatee and sideburns, and often grins effervescently. Kaji keenly told me about his other hobbies, besides number puzzles. For instance, he collects rubber bands, and on a recent trip to London found what to him amounted to a glorious cache – a 25g pack of branded rubber bands from WH Smith and a 100g pack from an independent stationer. He also amuses himself by photographing arithmetically gratifying car licence plates. In Japan, licence plates consist of two numbers followed by another two numbers. Kaji carries a small camera at all times and snaps every registration he sees for which the first pair multiplied by each other equals the second pair.

Assuming that no Japanese car has a 00 for the second pair of digits, each plate Kaji photographs is a line in the times tables of the digits 1 to 9. For instance, 11 01 can be thought of as 1×1 = 1. Likewise, 12 02 is 1×2 = 2. We can carry on the list, and work out that there are 81 possible combinations. Kaji has already collected more than 50. Once he has gathered the full set of times tables, he plans to exhibit them in a gallery.

 

The idea that numbers can entertain is as old as maths itself. The ancient Egyptian Rhind Papyrus, for example, contains the following list as part of the answer to problem 79. Unlike the other problems in the papyrus, this one has no apparent practical application.

Kaji snaps 3 × 5 = 15 in a Tokyo car park.

 

Houses	7
Cats	49
Mice	343
Spelt	2401*
Hekat†	16,807
Total	19,607

 

The list is the inventory of seven houses, each of which had seven cats, each of which ate seven mice, each of which ate seven grains of spelt, each of which came from a separate hekat. The numbers form a geometric progression – which is a sequence where each term is calculated by multiplying the previous term by a fixed number, in this case, seven. There are seven times more cats than houses, seven times more mice than cats, seven times more grains of spelt than mice, and seven times more hekats than grains of spelt. We could rewrite the total number of items as 7 + 7² + 7³ + 7⁴ + 7⁵.

It wasn’t just the Egyptians, however, who found such a sequence irresistible. Almost exactly the same sum reappeared in the early nineteenth century in a Mother Goose nursery rhyme:

The verse is the most famous trick question in English literature since, presumably, the man and his phalanx of females and confined felines were coming from St Ives. Irrespective of the direction of travel, however, the total number of kits, cats, sacks and wives is 7 + 7² + 7³ + 7⁴, which is 2800.

Another, less well-known, appearance of the riddle is as a problem in Leonardo Fibonacci’s Liber Abaci, from the thirteenth century. This version involved seven women on their way to Rome with increasing numbers of mules, sacks, loaves, knives and sheaths. The extra 7⁶ brings the series to 137,256.

What is the allure of rising powers of seven that they have appeared in such different ages and contexts? Each case demonstrates the turbo-charged acceleration of geometric progressions. The rhyme is a poetic way of showing how quickly small numbers can lead to big ones. On first hearing, you think there might be a fair amount kits, cats, sacks and wives – but not almost 3000 of them! Likewise, the playful problems set in the Rhind Papyrus and the Liber Abaci express the same mathematical insight. And the number 7, though it would seem like it should have some special quality to make it so common across these problems, is rather irrelevant. When you multiply any number by itself a few times, the sum quickly reaches a counter-intuitively high amount.

Even when multiplying the lowest number possible, 2, by itself, the sum swirls to the heavens at a dizzying pace. Place one grain of wheat on the corner square of a chessboard. Place two grains on the adjacent square, and then start filling up the rest of the board by doubling the grains of wheat per square. How much wheat would you need to fill the final square? A few truckloads, or a container, maybe? There are 64 squares on a chessboard, so we have doubled up 63 times, meaning that the number is 2 multiplied by itself 63 times, or 2⁶³. In grains, this number is about 100 times more than the world’s current annual wheat production. Or, to consider it another way, if you started counting a grain of wheat per second at the very moment of the Big Bang 13 billion or so years ago, then you would not even have counted up to a tenth of 2⁶³ by now.

 

Mathematical riddles, rhymes and games are now collectively known as recreational maths. It is a wide-ranging and vibrant field, an essential feature of which is that the topics are accessible to the dedicated layperson, even though they might touch on impossibly complicated theory. Or they might not even involve theory at all, but rather merely kindle an appreciation of the wonder of numbers – such as the thrill of collecting pictures of licence plates.

A landmark event in the history of recreational maths is said to have taken place by the banks of the Yellow River in China around 2000 bc. According to legend, Emperor Yu saw a turtle creep out of the water. It was a divine turtle, with black and white dots on its underbelly. The dots denoted the first nine numbers and formed a grid on the turtle’s belly that (if the dots were instead written as Arabic numerals) looked like A:

A square like this one, that contains all the consecutive numbers starting from 1 and arranged so that all the rows, columns and corner-to-corner diagonals add up to the same total, is known as a magic square. The Chinese called this square the lo shu. (Its rows, columns and diagonals all add up to 15.) The Chinese believed that the lo shu symbolized the inner harmonies of the universe and used it for divination and worship. For example, if you start at 1 and draw a line between the numbers of the square in order, you map out the pattern that can be seen in B and the figure opposite, which shows the instructions for the movement of Taoist priests through a temple. The pattern, which is called the yubu, also underlies some of the rules of feng shui, the Chinese philosophy of aesthetics.

Taoist woodblock print with the yubu.

China was not the only culture to see the mystical side of the lo shu. Magic squares have been objects of spiritual importance for Hindus, Muslims, Jews and Christians. Islamic culture found the most creative uses. In Turkey and India vgins were required to embroider magic squares on the shirts of warriors. And if a magic square were placed over the womb of a woman in labour, it was believed that the birth would be an easier one. Hindus wore amulets with magic squares as protective charms, and Renaissance astrologers associated them with the planets in our solar system. It is easy to mock a predisposition for the occult in our ancestors, yet modern man can understand their fascination with magic squares. Both simple and yet subtly complex, a magic square is like a numerical mantra, an object of endless contemplation and a self-contained expression of order in a disordered world.

Melencolia I: Dürer’s famous woodcut shows an angel lost in thought surrounded by mathematical and scientific objects, such as a compass, a sphere, a set of scales, an hourglass and a magic square. Art historians, especially those with a mystical bent, have long pondered the symbolism of the geometrical object in the middle left of the image, which is known as ‘Dürer’s solid’ mathematicians have long pondered the mystery of how on earth to construct it.

One of the pleasures of magic squares is that they are not restricted to 3 × 3 grids. A famous example of a 4 × 4 square comes from the work of Albrecht Dürer. In Melencolia I (shown opposite), Dürer included a 4 ×4 square that is best known for containing the year in which he engraved it: 1514.

Dürer’s square, in fact, is übermagic. Not only do the rows, columns and diagonals add up to 34, but so do the combinations of four numbers marked by dots and linked in the squares below.

The patterns Dürer’s square produces are amazing, and the more you look, the more you find. For example, the sum of the squares of the numbers on the first and second rows adds up to 748. You get the same total by adding up the squares of the numbers in rows 3 and 4, or the squares of the numbers in rows 1 and 3, or the squares of the numbers in rows 2 and 4, or the squares of the numbers in both diagonals. Wow!

For further amazement, rotate Dürer’s square by 180 degrees, then subtract 1 from the squares containing 11, 12, 15 and 16. The result is the following:

The image is from the side of the Sagrada Família cathedral in Barcelona, designed by Antoni Gaudí. Gaudí’s square is not magic, as two numbers are repeated, but it is still pretty special. The columns, rows and diagonals now all add up to 33: the age of Christ at his death.

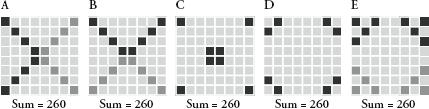
Hours of fun can be had by playing around with magic squares, and marvelling at the patterns and harmonies. In fact, no other area of non-practical maths has attracted as much attention from amateur mathematicians over such a long period. In the eighteenth and nineteenth centuries, literature on magic squares flourished. One of the most notable enthusiasts was Benjamin Franklin, one of the Founding Fathers of the United States who, as a young clerk of the Pennsylvania Assembly, got so bored during debates that he would construct his own squares. His best-known square is the 8 × 8 variation shown opposite, which he is said to have invented as a boy. In this square Franklin included one of his own enhancements to the theory of magic squares: the ‘broken diagonal’, which are the number in the black squares and grey squares, shown in A and B below. While his square isn’t a proper magic square because the full diagonals don’t add up to the number 260, his newly invented broken diagonals do. The sums of the black squares in C and D and E, and the sum of the grey squares in E and, of course, the sum of every row and column, also add up to 260.

In a letter published in 1769, Benjamin Franklin commented about a book of magic squares: ‘In my younger days…I had amused myself in making these kind of magic squares and, at length, had acquired such a knack at it, that I could fill the cells of any magic square, of reasonable size, with a series of numbers as fast as I could write them, disposed in such a manner, as that the sums of every row, horizontal, perpendicular, or diagonal, should be equal; but not being satisfied with these, which I looked on as common and easy things, I had imposed on myself more difficult tasks, and succeeded in making other magic squares, with a variety of properties, and much more curious.’ He then introduced the square above, printed in his Experiments and Observations on Electricity, made at Philadelphia in America , in 1769.

Franklin’s square contains even more beguiling symmetries. The sum of the numbers in every 2 × 2 subsquare is 130, as is the sum of any four numbers that are arranged equidistant from the centre. Franklin is also said to have invented another square in his forties. Over the course of a single evening, he composed an incredible 16 × 16 square that he claimed was ‘the most magically magical of any magic square ever made by any magician’. (It is in the appendices.)

 

One of the reasons for the enduring popularity of constructing magic squares is that there is a surprising number of them. Let’s count them, starting from the smallest: there is just one magic square in a 1 × 1 grid: the number 1. There are no magic squares with four numbers in a 2 × 2 grid. There are eight ways to arrange the digits 1 to 9 so that the resulting 3 × 3 square is magic, but each of these eight squares is really the same square either rotated or reflected, so it’s conventional to say that there is only one true 3 × 3 magic square. The figure on the opposite page shows how to generate each possibility, starting with the lo shu.

Amazingly, after three, the number of magic squares that can be made grows staggeringly fast. Even after reducing the number by ignoring rotations and reflections, it is possible to make 880 magic squares in a 4 × 4 grid. In a 5 × 5 grid the number of magic squares is 275,305,224, a result calculated in 1973, and only through the use of a computer. And though this number seems astronomically high, it is, in fact, tiny compared to the number of all possible arrangements of the digits 1 to 25 in a 5 × 5 square. The total number of arrangements is calculated by multiplying 25 by 24 by 23 and so on until 1, which is about 1.5 followed by 25 zeros, or 15 septillions.

The number of 6 × 6 magic squares is not even known, although it is likely to be in the order of 1 followed by 19 zeros. The number is so huge that it exceeds even the total number of grains of wheat in the chessboard exampe on chapter 6.

 

Magic squares have not been just the province of amateurs. At the end of his life, the eighteenth-century Swiss mathematician Leonhard Euler became curious about them. (He was almost totally blind by this time, which makes his research into what is an essentially spatial application of numbers especially awe-inspiring.) In particular, his work included the study of a modified version in which each number or symbol in the grid appears exactly once in each row and column. He called it a Latin square.

Latin squares.

Unlike magic squares, Latin squares have several practical applications. They can be used to work out brackets in round-robin sports tournaments, in which every team has to play every other team, and in agriculture they form a handy grid that enables a farmer to test, for example, several different fertilizers on a piece of land to see which works best. If the farmer has, say, six products to test and he divides the land into a 6 × 6 square, distributing each product in the pattern of a Latin square ensures that any change in soil conditions affects each treatment equally.

 

Maki Kaji, the Japanese puzzle-maker I introduced at the start of the chapter, ushered in a new era of number-square fascination. The idea came to him as he was browsing an American puzzle magazine. As a non-English-speaker, he scanned pages of incomprehensible word games before stopping when he came across an intriguing-looking grid of numbers. The puzzle, entitled ‘Number Place’, was a partially completed 9 × 9 Latin square that used the digits 1 to 9. Based on the rules that each number was allowed to appear only once per row and per column, the would-be solver needed to figure out how to fill in the missing gaps using a process of logical deduction. Solvers were aided by a further condition: the square was divided into nine 3 × 3 subsquares, each of which was marked in bold. Each number 1–9 was allowed only once per subsquare. Kaji solved Number Place and got excited – this was precisely the sort of puzzle he wanted to put in his new magazine.

Number Place, which had made its first appearance in 1979, was the creation of Howard Garns, a retired architect and puzzle enthusiast from Indiana. Though he enjoyed solving Garns’s puzzle, Kaji decided to redesign it so that the numbers provided were distributed in a symmetrical pattern around the grid, matching the format used for crosswords. He called his version Sudoku, the Japanese for ‘the number must appear only once’.

Sudoku appeared in the early issues of Kaji’s puzzle magazine, which launched in 1980, but Kaji said it attracted no attention. It was only once the puzzle travelled overseas that it spread like wildfire.

Just as a Japanese-speaker with no English could understand Number Place, so an English-speaker with no Japanese could understand Sudoku. In 1997 a New Zealander named Wayne Gould walked into a bookstore in Tokyo. Although he was initially disoriented by the fact that everything was in Japanese, his eyes eventually landed on something familiar. He saw a book cover with what looked like a crossword grid with numbers on it, and though the image was obviously some kind of puzzle, he didn’t instantly understand the rules. Stll, he bought the book, thinking he’d figure it out later. On a holiday in southern Italy he worked backwards until he cracked the puzzle. Gould had just retired from being a judge in Hong Kong and was teaching himself how to program computers, so he decided he would try to write a program that generated Sudokus. A top programmer might take a couple of days for this task. It took Gould six years.

But the effort was worth it, and in September 2004 he persuaded New Hampshire’s Conway Daily Sun to publish one of his puzzles. It was an immediate success. The following month he decided to approach the British national press. Gould thought the most effective way to pitch his idea was to present a mock-up of that day’s paper with the Sudoku already in it. He knew enough about forgery from covering trials in Hong Kong to make a convincing fake of The Times’s second section, and took it to the paper’s head office. After waiting a few hours in reception, Gould showed them his dummy paper, and they seemed to like it. In fact, immediately after he left, a Times executive sent Gould an email asking him not to show the Sudoku puzzles to anyone else. Two weeks later the puzzle first appeared, and three days after that, the Daily Mail introduced its own version. In January 2005 the Daily Telegraph joined the game, and not long afterwards every British newspaper had to have a daily puzzle to keep up with the competition. That same year the Independent reported a 700 percent rise in UK pencil sales, and attributed it to the craze. By summer, shelves of Sudoku books appeared in bookshops, newsagents and airports, and not just in the UK but around the world. At one point in 2005 six of the top 50 books on USA Today’s bestseller list were Sudoku titles. By the end of the year the puzzle had spread to 30 countries, and Time magazine named Wayne Gould one of the 100 people who most shaped the world that year, along with Bill Gates, Oprah Winfrey and George Clooney. By the end of 2006, Sudokus were being published in 60 countries; and by the end of 2007, in 90. According to Maki Kaji, the number of regular Sudoku players now exceeds 100 million people.

 

Completing any puzzle is immensely gratifying to the ego, but part of the extra allure of completing a Sudoku is the inner beauty and balance of the perfect Latin square that gives it its form. Sudoku’s success is testament to an age-old, cross-cultural fetish for number squares. And unlike many other puzzles, its success is also a remarkable victory for mathematics. The puzzle is maths by stealth. Although Sudoku contains no arithmetic, it does require abstract thought, pattern recognition, logical deduction and the generation of algorithms. The puzzle also encourages an aggressive attitude towards problem-solving, and fosters an appreciation of mathematical elegance.

For instance, as soon as you understand the rules of Sudoku, the concept of a unique solution is remarkably clear. For every pattern of numbers in the grid at the start, there is only one possible final arrangement for the numbers in the empty spaces. However, it is not the case that every partially filled grid has a unique solution. It is perfectly possible that a 9 × 9 square with some numbers filled in has no solutions, just as it is perfectly possible that it has many solutions. When Sky TV launched a Sudoku show, they drew what they claimed was the world’s largest Sudoku by cutting a 275 × 275ft grid out of a chalk hillside in the English countryside. However, the given numbers were placed in such a way that there were 1905 valid ways to complete the square. The roclaimed largest Sudoku did not have a unique solution, and therefore was not a Sudoku at all.

The branch of mathematics that involves the counting of combinations, such as all the 1905 solutions to Sky TV’s faux Sudoku, is called combinatorics. It is the study of permutations and combinations of things, such as grids of numbers, but also, famously, the schedules of travelling salesmen. Let’s say, for instance, that I’m a travelling salesman and I have 20 shops to visit. In what order should I visit them so that my total distance is the shortest? The solution requires me to consider all the permutations of paths between all the shops, and is a classic (and extremely difficult) combinatorial problem. Similar problems arise throughout business and industry, for example in scheduling flight departure times at airports or having an efficient postal sorting system.

Combinatorics is the branch of maths that most consistently deals with extremely high numbers. As we saw with magic squares, a small set of numbers can be rearranged in an astonishingly large number of ways. Though they both share square grids, there are fewer Latin squares than magic squares for the same size of grid, though the number of Latin squares is still colossal. The number, for example, of 9 × 9 Latin squares is 28 digits long.

How many possible Sudokus are there? If a 9 × 9 Latin square is to qualify as a finished Sudoku grid, the 9 subsquares must also include every digit, and this reduces the total of Sudoku-ready 9 × 9 squares to 6,670,903,752,021,072,963,960. Many of these grids, however, are different versions of the same square when reflected or rotated (as I showed with the 3 × 3 magic square on chapter 6). Eliminating squares that are rotations and reflections, the number of distinct possible finished Sudoku grids is about 5.5 billion.

Still, this is not the total number of possible Sudokus, which is much larger since each finished grid will be the solution to many Sudokus. For example, a Sudoku in a newspaper has one unique solution. Once you fill in one of the squares, however, you are creating a new grid with a new set of givens, in other words a new Sudoku with the same unique solution, and so on for each square you fill in. So if a Sudoku has, say, 30 given numbers, then we will be able to create another 50 Sudokus with the same unique solution until we complete the grid. (That’s one new Sudoku for each extra number, until there are 80 givens in the 81-square grid.) Finding the total number of Sudokus is not that interesting since what we will find is that most of these Sudokus have grids with very few blank spaces in them, which is not in the spirit of the puzzle. Instead, mathematicians get much more excited about the number of digits you can leave in the square. The number one combinatorics question about Sudoku is what is the least amount of numbers you can leave in the square so that there is only one way to fill in the grid?

The Sudokus published in newspapers usually include around 25 given numbers. To date, no one has found a Sudoku that has a unique solution with fewer givens than 17. In fact, 17-clue Sudokus inspire something of a combinatorics cult. Gordon Royle, of the University of Western Australia, maintains a database of 17-clue Sudokus, and receives three or four new ones every day from puzzle-makers around the world. So far, he has collected almost 50,000. But even though he is the world’s expert on 17-clue puzzles, he says he doesn’t know how close he is to finding the total number of possible puzzles. ‘A while ago I would have said that we were close to the end, but then an anonymous contributor sent in nearly 5000 new ones,’ he said. ‘We never really worked out how 8220;anon17” could do it, but it clearly involved a clever algorithm.’

In Royle’s opinion, no one has found a 16-clue Sudoku because, as he said, ‘Either we are not clever enough or our computers are not powerful enough.’ Most likely, anon17 didn’t reveal his method because he was using someone else’s very large computer when he wasn’t supposed to. Answering combinatorics problems often relies on giving the hard work of number-crunching over to a computer. ‘The total possible space of 16-clue possible puzzles is far too vast for us to explore more than a tiny proportion of it without some new theoretical ideas,’ Royle claimed. But he has a gut feeling that no 16-clue Sudokus will ever be found, adding: ‘We have so many 17-clue puzzles now it would really be a bit strange if there was a 16-clue puzzle that we had not stumbled across.’

 

Maki Kaji’s business card has the words Godfather of Sudoku. Wayne Gould describes himself as the Stepfather of Sudoku. I finally met up with Gould over coffee in a West London deli. He was wearing a New Zealand rugby top and had a typically antipodean, easygoing manner. Gould has a gap between his front teeth, which together with his thick glasses, short silvery hair and youthful enthusiasm reminded me of a young university lecturer rather than a former judge. Sudoku has transformed Gould’s life. He has been busier in retirement than he ever was before. He supplies puzzles for free to more than 700 newspapers in 81 countries, earning money from selling his program and books, which he says gives him only about 2 percent of the global Sudoku market. Still, Sudoku has earned him a seven-figure fortune. And he is a celebrity. When I asked him how his wife felt about his unexpected fame, he paused. ‘We separated last year,’ he stuttered. ‘After 32 years of marriage. Maybe it was having all that money. Maybe it gave her a freedom she never knew she had.’ Through the silence the message I heard was a heartbreaking one: he might have launched a global craze, but the adventure had come at too high a personal cost.

 

I’ve always thought that one reason for Sudoku’s success is its exotic name, which resonates with the romance of superior Oriental wisdom, despite the fact that the American Howard Garns came up with the idea in Indiana. In fact, there is a tradition of puzzles coming from the East. The very first international puzzle craze dates from the early nineteenth century, when European and American sailors returning from China brought home sets of geometrical shapes, typically made of wood or ivory, that had seven pieces – two large triangles, two small triangles, a medium-sized triangle, a rhomboid and a square. Put together, the pieces made up a larger square. Accompanying the sets were booklets with dozens of outlines of geometrical shapes, human figures and other objects. The aim of the puzzle was to use all seven of the pieces to create each printed silhouette.

The puzzle had originated with the Chinese tradition of arranging tables of different shapes for banquets. One Chinese book, from the twelfth century, showed 76 banquet placements, many of which were made to look like objects, such as a fluttering flag, a range of mountains and flowers. At the turn of the nineteenth century a Chinese writer with the playful nickname Dim-Witted Recluse adapted this ceremonial choreography for finger-sized geometrical blocks and put the figures in a book, Pictures Using Seven Clever Pieces.

Tangram figures through the ages.

Originally called the Chinese Puzzle, the sets later gained the name ‘tangram’. The first book of tangram puzzles to be published outside China was printed in London in 1817. Immediately, the book started a fad. Between 1817 and 1818 dozens of tangram books came out in France, Germany, Italy, the Netherlands and Scandinavia. Cartoonists of the day captured the craze by portraying men unwilling to go to bed with their wives, chefs unable to do the cooking and doctors refusing to attend patients because they were too busy rearranging triangles. The craze was more pronounced in France, perhaps because one of the books claimed that the puzzle was Napoleon’s favourite amusement during his exile on the South Atlantic island of St Helena. The former emperor was an early adopter since ships stopped off there on their way back from Asia.

I love the tangram. Men, women and animals magically come to life. By a slight repositioning of just one piece the personality of the figure changes entirely. With their angular and often grotesque contours, the figures are wonderfully suggestive. The French took this personification to an extreme by actually painting images within the silhouettes.

It is hard to believe how engrossing the puzzle is until you have tried it out. In fact, though it looks easy, solving tangram problems can be surprisingly difficult. The shapes can easily deceive, as when two similar-looking silhouettes have totally different underlying structures. The tangram can serve as a warning against complacency, reminding you that the essence of objects may not always be what you first see. Take a look at the following tangram figures. It looks as if a small triangle has been removed from the first to make the second. In fact, both figures use all the pieces and they are arranged in completely different ways.

In the mid nineteenth century, tangrams were embraced by schools, though they still remained an adult pastime. The German company Richter rebranded the tangram as the Kopfzerbrecher, or brain-buster, and, due to the product’s success, introduced more than a dozen similar rearrangement puzzles with different shapes cut into different pieces. During the First World War, Richter puzzles became a much-loved diversion for troops stuck in the trenches. Demand was so great that another 18 puzzles were launched. One of them was called the Schützengraben Geduldspiel – the trench patience game – which contained military shapes such as a Zeppelin, a revolver and a grenade. Some of the figures were devised by soldiers, who had sent the ideas in from the front.

First World War advert for Lott’s brick puzzles.

Before the war, Richter had licensed its puzzles to the Lott’s Brick Company in the UK. It was not only German soldiers who spent their days on the front solving tangram spin-offs; a few miles away in the Allied trenches, the British were doing exactly the same.

As each generation has created new figures, the tangram has never really gone out of fashion in almost 200 years. You can still buy the puzzle in toyshops and bookstores. The stock of published outlines is now more than 5900.

 

Despite the association of the tangram with puzzles of this kind, it was not the world’s first rearrangement puzzle. In ancient Greece the similar stomachion divided a square into 14 pieces. (Stomachi means ‘stomach’, and the name is thought to be a result of the bellyache that the puzzle induced, although not from ingesting the pieces.) Archimedes wrote a treatise on the stomachion, only a fraction of which survives. Based on this fragment, it has been suggested that the treatise was an attempt to calculate the number of different ways the pieces of the stomachion could be positioned to make a perfect square. Only recently was this particular ancient problem solved. In 2003 the computer scientist Bill Cutler found that there are 536 ways (excluding solutions that are identical under rotation or reflection).

The stomachion , which is also known as the ‘loculus of Archimedes’.

Since the time of Archimedes a keen interest in recreational puzzles has been a trait shared by many mathematicians. ‘Man is never more ingenious than in the invention of games,’ said Gottfried Leibniz, for instance, whose love of peg solitaire resonated with his obsession with binary numbers: a hole either has a peg in it or it doesn’t, it is either a 1 or a 0. However, the most playful of the great mathematicians was Leonhard Euler, who, in order to crack an eighteenth-century brainteaser, invented a whole new branch of mathematics.

In Königsberg, the former Prussian capital that is now the Russian city of Kaliningrad, there used to be seven bridges that crossed the River Pregel. Locals wanted to know if it would be possible to make a journey across all seven bridges without crossing any bridge more than once.

To come up with a proof that a circuit of this kind was impossible, Euler created a graph in which each landmass was represented by a dot, or node, and each bridge by a line, or link. He worked out a theorem that related the number of links touching each node to whether it was possible to make a circuit of the graph, and in this case it was impossible.

The conceptual leap Euler made was to realize that what was important to solve the problem was not information about the exact position of the bridges, but how they were connected. The London Underground map borrows this idea: it is not geographically accurate, but is faithful to how the Tube lines are linked together. Euler’s theorem launched graph theory, and presaged the development of topology, a very rich area of maths that studies the properties of objects that do not change when the object is squeezed, twisted or stretched.

Königsberg in the eighteenth century: as a map and as a graph.

Fascination in 1817 with tangrams was nothing compared with the extraordinary levels of excitement generated by the world’s second international puzzle craze. From the day in December 1879 when the Fifteen puzzle launched in a Boston toyshop, manufacturers couldn’t meet the demand. ‘Neither the wrinkled front of age nor the cherubic brow of childhood is proof against the contagion,’ declared the Boston Post.

The Fifteen puzzle consisted of 15 square wooden blocks placed in a square carton so that the blocks made a × 4 square with one square missing. The blocks were numbered 1 to 15 and put in the box randomly. The aim of the puzzle was to slide the blocks around the 4 × 4 square using the empty space and finish with them positioned in numerical order. Playing with the Fifteen puzzle was so addictive and fun that the fad soon spread from Massachusetts to New York, and then across the United States. ‘It has swept over the land from East to West with the violence of the sirocco, scorching men’s brains as it passed, and apparently making them temporarily insane,’ quivered the Chicago Tribune. According to the New York Times, no pestilence ‘has ever visited this or any other country which has spread with [such] awful celerity’.

The puzzle soon went overseas, with one shop in London reportedly selling nothing else. Within six months it had reached the other side of the world. ‘Not a few have already been driven insane,’ claimed a letter in the Otago Witness, New Zealand, on 1 May 1880.

The Fifteen puzzle was initially known as the Gem puzzle.

The Fifteen puzzle was the creation of Noyes Chapman, a postmaster in upstate New York, who almost two decades previously had been trying to make a physical model of a 4 × 4 magic square. He made small wooden squares for each of the 16 numbers and fitted them snugly into a square box. When he realized that leaving out one block provided a space into which any adjacent block could be slid, he saw that trying to rearrange the numbers would make a particularly fun game. Chapman made a few versions for family and friends, but never capitalized on his invention. It was only when a savvy Boston carpenter decided to commercialize the puzzle that it finally took off.

The Fifteen puzzle was especially tormenting to those who attempted it because sometimes it was solvable and sometimes it was not. Once the blocks were randomly put in there seemed to be only two outcomes: either they could be rearranged in numerical order, or they could be rearranged so that the first three rows were in order but the last line went 13-15-14. The craze was fuelled, in part, by a desire to work out if it was possible to get from 13-15-14 to 13-14-15. In January 1890, a few weeks after the first puzzle went on sale, a dentist in Rochester, New York, placed an ad in the local paper offering a $100 prize and a set of false teeth to anyone who could prove it either way. He believed it was impossible – but needed some help with the maths.

Bafflement with the Fifteen puzzle spread from the world’s living rooms to the halls of academe, and once the professionals got involved, the puzzle went from insanity-inducing unsolvable to satisfactorily unsolvable. In April 1890 Hermann Schubert, one of the outstanding mathematicians of his day, published in a German newspaper the earliest proof that 13-15-14 was an unsolvable position. Shortly thereafter, the recently founded American Journal of Mathematics also published a proof, confirming that half of the total of all starting positions in the Fifteen puzzle will produce a final solution of 13-14-15, and half will end up 13-15-14. The Fifteen puzzle remains the only international craze in which the puzzle does not always have a solution. No wonder it drove people mad.

Like the tangram, the Fifteen puzzle has not totally disappeared. It was the forerunner of the sliding-block puzzles that are still found in toyshops, Christmas crackers and corporate marketing gift packs. In 1974 a Hungariann was devising ways to improve the puzzle when he was struck with the idea of reinventing it in three dimensions. The man, Ernö Rubik, came up with his prototype, the Rubik’s Cube, which went on to become the most successful puzzle in history.

 

In his 2002 book The Puzzle Instinct, the semiotician Marcel Danesi wrote that an intuitive ability to solve puzzles is part of the human condition. When we are presented with a puzzle, he explains, our instincts drive us to find a solution until we are satisfied. From the riddle-asking sphinx of Greek mythology to the detective mystery, puzzles are a common feature across time and cultures. Danesi argues that they are a form of existential therapy, showing us that challenging questions can have precise solutions. Henry Ernest Dudeney, Britain’s greatest puzzle-compiler, described solving puzzles as basic human nature. ‘The fact is that our lives are largely spent in solving puzzles; for what is a puzzle but a perplexing question? And from our childhood upwards we are perpetually asking questions or trying to answer them.’

Puzzles are also a wonderfully concise way of conveying the ‘wow’ factor of maths. Often they require lateral thinking, or rely on counter-intuitive truths. The sense of achievement gained from solving a puzzle is an addictive pleasure; the sense of failure from not solving one almost unbearably frustrating. Publishers realized pretty quickly that fun maths had a market. Amusing and Entertaining Problems that Can Be Had with Numbers (very useful for inquisitive people of all kinds who use arithmetic) by Claude Gaspard Bachet came out in France in 1612. It included sections on magic squares, card tricks, questions in non-decimal bases, and think-of-a-number problems. Bachet was a serious scholar who translated Diophantus’s Arithmetica. But his popular maths book was arguably more influential than his academic work. All subsequent puzzle books are indebted to it, and it has kept its relevance for centuries, republished most recently in 1959. A defining feature of maths, even recreational maths, is that it never goes out of date.

In the mid nineteenth century American newspapers started to print chess problems. One of the first, and most precocious, devisers of these problems was Sam Loyd. A New Yorker, Loyd was just 14 when he had his first conundrum printed in a local paper. By 17 he was the most successful and widely celebrated deviser of chess problems in the US.

He moved on from chess to mathematically based puzzles, and by the end of the century was the world’s first professional puzzle-compiler and impresario. He published widely in the American media, and once claimed that his columns attracted 100,000 letters a day. However, we should take his figure with a pinch of salt. Loyd cultivated the kind of playful attitude towards the truth that one expects of a professional riddler. For a start, he claimed he had invented the Fifteen puzzle, which was taken to be true for more than a century until in 2006 historians Jerry Slocum and Dic Sonneveld properly traced its origin to Noyes Chapman. Loyd also revived interest in the tangram with The 8th Book of Tan Part I, a version of an ancient text about the supposed 4000-year history of the puzzle. The book was a spoof, even though it was initially taken seriously by academics.

Loyd had a unique brilliance at turning mathematical problems into entertaining, distinctively illustrated puzzles. His most genial creation was invented for the Brooklyn Daily Eagle in 1896. The ‘Get off the Earth’ puzzle widely i popular that it was later adopted as a publicity gimmick by several brands, including The Young Ladies Home Journal, the Great Atlantic & Pacific Tea Company and the Republican platform for the 1896 presidential election. (Although its message was not a manifesto pledge.) The puzzle is an image of Chinese warriors positioned around the Earth, which is on a disc made out of card that can be spun around its centre. When the arrow is pointing NE there are 13 warriors, but turn the disc so the arrow points NW and there are only 12. The puzzle is confusing. There really are 13 warriors, then – in a flash – just 12. Which man has vanished and where does he go?

The trick operating in this puzzle is known as a geometrical vanish. It can also be demonstrated in the following way. The image on chapter 6 shows a piece of paper with ten vertical lines on it. When the piece of paper is cut along the diagonal line, the two sections can be realigned so that only nine lines are created. Where has the tenth line gone? What has happened is that the segments have been rearranged to form nine lines that are longer than the original line. If the lines in the first image have the length 10 units, then the length of the lines in the second image is 11 , since one of the original lines has been equally shared among the nine others.

What Sam Loyd did with ‘Get off the Earth’ is to curve the geometrical vanish so it was in a circular form, and in place of lines put Chinese warriors. There are 12 positions in his puzzle, akin to the 10 lines in the example overleaf. The position in the bottom left corner, where there are originally two warriors, is equivalent to the end lines of the vanish. When the arrow is moved from NE to NW, all the positions gain a bit more warrior, apart from the position with two warriors, which shrinks drastically, giving the impression that a whole warrior has been lost. In fact, it has just been redistributed around the others. Sam Loyd claimed that ten million copies of ‘Get off the Earth’ were produced. He became rich and famous, revelling in his reputation as the puzzle king of America.

Geometrical vanish: ten lines become nine.

Meanwhile, in Great Britain, Henry Ernest Dudeney was acquiring a similar reputation. If Loyd’s capitalist chutzpah and gift for self-publicity reflected the cut-and-thrust of turn-of-the-century New York, Dudeney embodied the more reserved English way of life.

From a family of Sussex sheep farmers, Dudeney started working at 13 as a clerk in the civil service in London. Bored with the job, he began to submit short stories and puzzles to various publications. Eventually he was able to devote himself to journalism full time. His wife Alice wrote bestselling romantic novels about life in rural Sussex – where, thanks to her royalties, the couple was able to live in luxury. The Dudeneys, dividing their time between the countryside and London, were part of a highbrow literary scene that included Sir Arthur Conan Doyle, the creator of Sherlock Holmes, probably the most iconic puzzle-solver in all literature.

It is thought that Dudeney and Sam Loyd first made contact in 1894, when Loyd posed a chess problem in the firm belief that no one would discover his 53-move solution. Dudeney, who was 17 years Loyd’s junior, found a solution in 50 moves. The men subsequently collaborated, but fell out when Dudeney discovered Loyd was plagiarizing his work. Dudeney despised Loyd so intensely that he equated him with the Devil.

While both Loyd and Dudeney were self-taught, Dudeney had a much finer mathematical mind. Many of his puzzles touched on deep problems – frequently predating academic interest. In 1962, for example, the mathematician Mei-Ko Kwan investigated a problem about the route a postman should take in a grid of streets so as to walk on every street and do it in the shortest route possible. Dudeney had framed – and solved – the same problem in a puzzle about a mine inspector walking through underground shafts almost 50 years earlier.

Dudeney also made unintended contributions to number theory. One of his puzzles, called Root Extraction, plays on the fact that the cube roots of the following numbers are also equal to the sum of the digits that make up those numbers:

 

1 = 1×1×1	1 = 1
512 = 8×8×8	8 = 5 + 1 + 2
4913 = 17×17×17	17 = 4 + 9 + 1 + 3
5832 = 18×18×18	18 = 5 + 8 + 3 + 2
17,576 = 26×26×26	26 = 1 + 7 + 5 + 7 + 6
19,683 = 27×27×27	27 = 1 + 9 + 6 + 8 + 3

 

Numbers with this property – and there are only six of them – are now known as Dudeney numbers. Another particular forte of Dudeney’s was the geometrical dissection, which is when a shape is cut up into pieces and reassembled into another shape, like the principle behind the tangram. Dudeney found a way of converting a square into a pentagon in six pieces. His method became a popular classic because for many years it had been thought that the minimum dissection of a square into a pentagon required seven pieces.

Dudeney also discovered a novel way to cut up a triangle and make it into a square in four pieces. And he realized that if the four pieces in his solution were hinged together, they could be assembled in a chain – such that folding one way gets you a triangle and folding the other way gets you the square. He called this the Haberdasher’s Puzzle, since the shapes look like the leftover pieces of cloth that a haberdasher might h in his shop. The puzzle thus introduced the concept of a ‘hinged dissection’, and aroused such interest that Dudeney made one out of mahogany with brass hinges and presented it in 1905 at a meeting of the Royal Society in London. The Haberdasher’s Puzzle was Dudeney’s greatest legacy and has fascinated and delighted mathematicians for more than a century.

The Haberdasher’s Puzzle.

One mind that was especially enthralled by the Haberdasher’s Puzzle belonged to the Canadian teenager Erik Demaine. Demaine, who was such a prodigy that by the time he was 20 he was already a professor at MIT, was most interested in the ‘universality’ of the problem. Is it possible, he wondered, to dissect any straight-sided shape and then hinge the pieces together in a chain so it can be folded into any other straight-sided shape of equal area? He spent ten years working on the problem and in March 2008, aged 27, announced the solution to a very receptive audience of puzzle-lovers in the ballroom of an Atlanta hotel.

Demaine is tall and skinny, with a fluffy beard and fuzzy dark-blond ponytail. On to a big screen behind him he projected an image of the Haberdasher’s Puzzle. He said that he had recently decided to attack the problem with his PhD students. ‘I didn’t believe it was true,’ he said. Contrary to his expectation, however, he and his students found that you can transform any polygon to any other polygon of equal area through a Haberdasher’s Puzzle-style hinged dissection. The hall started clapping – a rare occurrence in the upper reaches of computational geometry. But in puzzle land this was about as exciting a breakthrough as you can get – the solution to an iconic problem by one of the cleverest minds of his generation.

The Atlanta conference, called the Gathering for Gardner, was the most appreciative audience possible for Demaine’s talk. The Gathering is the world’s premier jamboree for mathematicians, magicians and puzzle people. It is a biannual homage to the man who revolutionized recreational mathematics in the second half of the last century. Martin Gardner, now 93 years old, wrote a monthly maths column in Scientific American between 1957 and 1981. This was a period of great scientific advances – space travel, information technology and genetics – yet it was Gardner’s lively and lucid prose that really caught readers’ imaginations. His column covered subjects from board games to magic tricks, from numerology to early computer games, and often ventured into tangential areas such as linguistics and design. ‘I thought [Gardner] had a playful respect for mathematics that is often lost in mathematical circles,’ Demaine told me when I spoke to him after his talk. ‘People tend to be too serious. My aim is to make everything I do fun.’

As a boy, Demaine was introduced to Gardner’s columns through his father, a glass-blower and sculptor. The Demaines, who often publish mathematical papers together, embody Gardner’s interdisciplinary spirit. Erik is a pioneer of computational origami, a field both mathematical and artistic, and some of the Demaines’ origami models have even been exhibited in New York’s Museum of Modern Art. Demaine considers maths and art parallel activities, which share an ‘aesthetic about simplicity and beauty’.

In Atlanta Demaine didn’t explain the details of his proof of the universality of Haberdasher’s Pzzle-style dissections to the audience, but he did say that dissecting one polygon so it can be rearranged and hinged to form another polygon isn’t always pretty – and will often be completely impracticable. Demaine is now applying his theoretical work on hinged dissections to make robots that can transform from one shape into another through folding – just like the heroes of the comic book and movie franchise Transformers, where robots morph into different types of machine.

The conference was the eighth Gathering for Gardner, or G4G, and its logo, designed by Scott Kim, is known as an inversion, or ambigram.

If you turn it upside-down, it reads exactly the same. Kim, a computer scientist turned puzzle-designer, invented this style of symmetrical calligraphy in the 1970s. Ambigrams do not have to be the same when rotated 180 degrees – any symmetry, or concealed writing, will do.

The writer Isaac Asimov called Kim ‘the Escher of the alphabet’, comparing him to the Dutch artist who played with perspective and symmetries to create self-contradictory images, most famously steps that appear to rise and rise until they reach where they began. Another similarity between Escher and Kim is that their work first reached a mass audience thanks to Martin Gardner.

Ambigrams were independently, and contemporaneously, conceived by the typographer and artist John Langdon. Mathematicians especially love this type of lettering since it is a witty take on their own search for patterns and symmetry. The author Dan Brown was introduced to ambigrams through his father Richard Brown, a maths teacher. Dan Brown commissioned Langdon to design the phrase Angels & Demons as an ambigram for his bestselling book of the same title, and named the lead character Robert Langdon in his honour. Langdon reappeared as the hero of The Da Vinci Code and The Lost Symbol. Ambigrams have also found a new niche – as body art. The quasi-gothic flourishes, often added to aid symmetry, together with the mystic energy of reading a name backwards and forwards, or upside-down and the right way up, coincides perfectly with the aesthetics of tattoos.

At the G4G it was impossible not to think that maths wards off the onset of dementia. Many of the guests were over 70 – some were in their eighties and even nineties. For more than half a century Gardner corresponded with thousands of readers, many of them famous mathematicians, and some became close friends. Raymond Smullyan, aged 88, is the world’s foremost expert on logical paradoxes. He began his talk: ‘Before I begin speaking, there is something I want to say.’ Willowy and charmingly scruffy, with flowing white hair and a feathery beard, Smullyan was frequently entertaining guests on the hotel piano. He also performed magic tricks on unsuspecting passers-by, and over dinner one evening brought the house down with a stand-up comedy routine.

In this tattoo designed by Mark Palmer, Angel becomes Devil when upside-down.

Aged 76, Solomon Golomb was less physically energetic than Smullyan but able to converse without talking in paradoxes. A soft-spoken grandfatherly figure, Golomb has made important discoveries in space communications, mathematics and electrical engineering. With the helping hand of Martin Gardner, he has also contributed to global pop culture. Early in his academic career Golomb came up with the idea of polyominoes, which are dominoes made out of more than two squares. A triomino is made of three, a tetromino out of four, and so on. An early Gardner column on how they fit together caused such international interest that Golomb’s book, Polyominoes, was translated into Russian, where it became a bestseller. One fan made a game that involved falling tetrominoes. That game, Tetris, became one of the world’s most enduring and best-loved computer games. Golomb, of course, has played Tetris for no longer than half an hour.

Another attendee, Ivan Moscovich, is the spitting image of an elderly Vincent Price. Impeccably dressed in a sharp dark suit, he had sparkling eyes, a pencil moustache and full head of brushed-back grey hair. For Moscovich, the attraction of puzzles is the creative thinking they require. He was born in what is now Serbia, and during the Second World War was interned at both Auschwitz and Bergen-Belsen. He believes he survived because of an innate creativity – he was continuously creating situations that ended up saving him. After the war, he turned into a workaholic puzzle-inventor. He likes to think constantly outside the box, to sidestep the inevitable. The motivation to continually come up with new ideas, he said, was an after-effect of the trauma of his own lucky escape.

Moscovich has had about 150 puzzles licensed and produced over the last half century, and compiled a book of puzzles that has been hailed as the greatest collection since the era of Loyd and Dudeney. Now 82, he clutched his latest creation: a sliding block puzzle called You and Einstein. The idea of the game is to slide blocks around a square grid to create a picture of Einstein. Moscovich’s clever twist is that each block has a slanted mirror that reflects the box to its side, meaning that what you think is the block is actually the reflection of something else. Moscovich told me he was excited that You and Einstein could be a global success.

The dream of Moscovich, like everyone in his industry, is, of course, to discover a new puzzle craze. There have been only four international puzzle crazes with a mathematical slant: the tangram, the Fifteen puzzle, the Rubik’s Cube and Sudoku. So far, the Cube has been the most lucrative. More than 300 million have been sold since Ernö Rubik came up with the idea in 1974. Apart from its commercial success, the gaudily coloured cube is a popular-culture evergreen. It is the nonpareil of puzzledom and, unsurprisingly, its presence was felt at the 2008 G4G. A talk on the Rubik’s Cube in four dimensions drew huge rounds of applause.

 

The original Rubik’s Cube is a 3 × 3 × 3 array made up of 26 smaller cubes, or cubies. Each horizontal and vertical ‘slice’ can be rotated independently. Once the pattern of the cubies is jumbled, the aim of the puzzle is to twist the slices so that each side of the cube has cubies of just one colour. There are six colours, one for each side. Moscovich told me Ernö Rubik was doubly brilliant. Not only was the idea of the cube a stroke of genius, but the way he made the blocks fit together was an outstandingly clever piece of engineering. When you dismantle a Rubik’s Cube there is no separate mechanical device holding it all together – each cubie contains a piece of a central, interlocking sphere.

As an object, the cube itself is sexy. It is a Platonic solid, a shape that has had iconic, mystical status since at least the ancient Greeks. The brand name was also a dream: catchy, with delicious assonance and consonance. The Rubik’s Cube had an Eastern exoticism too, not from Asia this time but from Cold War Eastern Europe. It sounded a lot like Sputnik, the original showpiece of Soviet space technology.

Another ingredient in its success was the fact that while solving the cube was not easy, the challenge did not put people off. Graham Parker, a builder from Hampshire, kept at it for 26 years until he achieved his dream. ‘I have missed important events to stay in and solve it and I would lay awake at night thinking about it,’ he said, after an estimated 27,400 hours of cube time. ‘When I clicked that last bit into place and each face was a solid colour I wept. I cannot tell you what a relief it was.’ Those who solved it over a more manageable period invariably wanted to solve it again, but quicker. Reducing one’s Rubik’s record became a competitive sport.

Speedcubing has only really taken off, however, since around 2000. One of the reasons is thanks to a sport even more quirky than the timed solving of mechanical puzzles. Speedstacking is the practice of stacking plastic cups in set patterns as fast as you can. It is both mesmerizing and awesome – the top stackers move so fast it is as if they are painting the air with plastic. The sport was invented in California in the 1980s as a way of improving children’s hand-eye coordination and general fitness. It is claimed that 20,000 schools worldwide now include it in their physical education curriculum. Speedstacking uses specialized mats that have a touch sensor linked to a stopwatch. The mats provided the speedcubing community for the first time with a standardized method to measure the time it takes to solve the cube, and are now used in all competitions.

Every week or so, somewhere around the world now hosts an official speedcubing tournament. To make sure that the starting position is sufficiently difficult in these competitions, the regulations stipulate that cubes must be scrambled by a random sequence of moves generated by a computer program. The current record of 7.08 seconds was set in 2008 by Erik Akkersdijk, a 19-year-old Dutch student. Akkersdijk also holds the record for the 2 × 2 × 2 cube (0.96secs), the 4 × 4 × 4 cube (40.05secs) and the 5 × 5 × 5 cube (1min 16.21 secs). He can also solve the Rubik’s Cube with his feet – his time of 51.36secs is fourth-best in the world. However, Akkersdijk really must improve his performance at solving the cube one-handed (33rd in the world) and blindfolded (43rd). The rules for blindfolded solving are as follows: the timer starts when the cube is shown to the competitor. He must then study it, and put on a blindfold. When he thinks it is solved he tells the judge to stop the stopwatch. The current record of 48.05secs was set by Ville Seppänen of Finland in 2008. Other speedcubing disciplines include solving the Rubik’s Cube on a rollercoaster, under water, with chopsticks, while idling on a unicycle, and during freefall.

The most mathematically interesting cube-solving category is how to solve it in the fewest moves possible. The contestant is given an officially scrambled cube and has 60 minutes to study the position before describing the shortest solving sequence he can come up with. In 2009 Jimmy Coll of Belgium claimed the world record: 22 moves. Yet this was just how many moves a very smart human needed to solve a jumbled-up cube after 60 minutes of thinking about it. Might he have been able to find a solution from the same configuration in a smaller number of moves if he had had 60 hours? The question that has most intrigued mathematicians about the Rubik’s Cube is this: what is the smallest number of moves, n, such that every configuration can be solved in n moves or less? As a mark of reverence, n in this instance is nicknamed ‘God’s number’v hei>

Finding God’s number is extremely complex because the numbers are so large. There are about 43×10¹⁸ (or 43 followed by 18 zeros) cube positions. If every unique cube position were stacked on top of each other, the tower of cubes would go to the sun and back more than eight million times. It would take far too long to analyse each position one by one. Instead, mathematicians have looked at subgroups of positions. Tomas Rokicki, who has been studying the problem for around two decades, has analysed a collection of 19.5 billion related positions and found ways of solving them in 20 moves or less. He has now looked at a million or so similar collections, each containing 19.5 billion positions, and found again that 20 moves was sufficient for a solution. In 2008 he proved that every other remaining Rubik’s Cube position is only two moves away from a position in one of his collections, giving an upper bound for God’s number of 22.

Rokicki is convinced that God’s number is 20. ‘I’ve solved, at this point, approximately 9 percent of all cube positions, and none of them has required 21 moves. If there are any positions that require 21 or more moves, they are exceptionally rare.’ Rokicki’s challenge is not so much theoretical but logistical. Running through sets of cube positions uses an incredible amount of computer memory time. ‘With my current technique, I would need about 1000 modern computers for about one year to prove [that God’s number] is 20,’ he said.

Cube maths has been a long-term hobby for Rokicki. When I asked him whether he has thought of investigating the maths of other puzzles, like Sudoku, he joked: ‘Don’t try to distract me with other shiny problems. Cube math is challenging enough!’

 

Ernö Rubik still lives in Hungary and rarely gives interviews. I did, however, get a chance to meet one of his former students, Dániel Erdély, in Atlanta. We met in a room in the hotel devoted to ‘mathematical objects’. Origami models, geometrical shapes and elaborate puzzles were laid out on tables. Erdély was there looking after his own creations: light blue objects about the size of cricket balls, ridged with intricate, swirling patterns. Erdély treated them with the affection that a dog breeder has for a litter of his puppies. He picked one up, pointed to the palm-sized planet’s crystalline landscape and said: ‘Spidrons.’

Erdély, like Rubik, is not a mathematician. Rubik is an architect, and Erdély is a graphic designer who studied graphic design at the Budapest College of Applied Arts, where Rubik was a professor. In 1979 Erdély attended classes given by Rubik. As homework for these classes he devised a new shape made out of a sequence of alternate, and shrinking, equilateral and isosceles triangles. He called the shape a ‘spidron’ because it curved like a spiral. By the time he left university, spidrons were his obsession. He played around with them endlessly, noticing that they could fit together like tiles in many aesthetically satisfying ways, in both two and three dimensions. About five years ago, a Hungarian friend helped write a program to generate spidrons on the computer. Their tessellating properties have subsequently captivated mathematicians, engineers and sculptors, and Erdély has made himself the shape’s globetrotting chaperon. He believes it could have applications in the design, for example, of solar panels. At the G4G he had met a man who runs a company that launches rockets. The spidron, he told me, may be about to go into space.

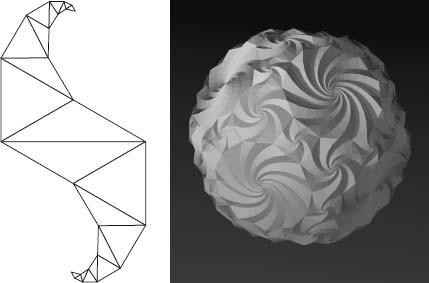
Spidron and spidron ball.

One afternoon the delegates of the conference relocated to the home of Tom Rodgers in the Atlanta suburbs. Rodgers, a businessman in late middle age, organized the first G4G in 1993. An admirer of Gardner’s since childhood, Rodgers’ initial idea was to have an event where the famously shy Gardner could meet some of the many readers he had corresponded with. He decided to invite guests from three specific areas of Gardner’s interest – maths, magic and puzzles. The gathering was such a success that a second one was organized in 1996. Gardner showed up to the first two but since then has been too frail to attend. Rodgers lives in a bungalow designed in Japanese style, surrounded by a forest of bamboo, pine and fruit trees that were in blossom when I visited. In the garden several guests were forming teams to build geometrical sculptures out of wood and metal. Others were attempting to solve a bespoke puzzle hunt whose clues were stuck to the house’s outside walls.

Suddenly, the shriek of Princeton University maths professor John Horton Conway grabbed everyone’s attention. Conway had a messy beard, a full head of silvery hair and was wearing a T-shirt with an equation on it. He is one of the most outstanding mathematicians of the last 50 years. He asked for everyone to bring him ten pine cones each so that he could count their spirals. Cone-classifying is a recent hobby of his; he has counted about 5000 of them since he started a few years ago.

Inside the house I met Colin Wright, an Australian who lives in Port Sunlight on the Wirral. With his schoolboyish ginger hair and glasses, he looks just how you might expect a mathematician to look. Wright is a juggler, which ‘seemed like the obvious thing to do after I learned to ride a unicycle’, he said. He also helped develop a mathematical notation for juggling, which might not sound like much, but has electrified the international juggling community. It turns out that with a language, jugglers have been able to discover tricks that had eluded them for thousands of years. ‘Once you have a language to talk about a problem, it aids your thought process,’ said Wright, as he took out some bean balls to demonstrate a recently invented three-ball juggle. ‘Maths is not sums, calculations and formulae. It is pulling things apart to understand how things work.’

I asked him if there was something self-indulgent, pointless or even wasteful about the finest minds in mathematics spending their time working on inconsequential pastimes like juggling, counting pine cones or even puzzle-solving. ‘You need to let mathematicians do what they do,’ he replied. ‘You genuinely never know what is going to be useful.’ He quoted the example of Cambridge professor G.H. Hardy, who in 1940 famously (and proudly) declared that number theory had no practical applications; in fact, it is now the basis of many internet security programs. Mathematicians have, according to Wright, been ‘unreasonably successful’ in finding applications to apparently useless theorems, and often years after the theorems were first discovered.

 

One of the most charming aspects of the G4G is that all guests are asked to bring a gift – ‘something you would want to give to Martin’. In fact, you are asked to bring 300 of your gift, since each guest is given a goody bag at the end, containing one of everyone else’s gift. The year I visited the goody bag included puzzles, magic tricks, books, CDs, gadgets and piece of plastic that can mke a Coke can talk. One bag was for Martin Gardner, and I took it to him.

Gardner lives in Norman, Oklahoma. The day I arrived storms were moving across the state. After a few wrong turns off the interstate, I found his home, an Assisted Living Center next to a Texan fast-food joint. The door to his room is only a few steps from the entrance, past a common area where a couple of the elderly residents was sitting and chatting. By Gardner’s door was a box of correspondence. He does not use email. He sends more letters than the rest of the home combined.

Gardner opened the door and invited me in. On the wall there was a portrait of him made out of dominoes, a large photograph of Einstein and an Escher original. Gardner was casually dressed in a green shirt and slacks. He had a soft, open complexion, with wisps of white hair, large tortoiseshell glasses and alert eyes. There was an ethereal aspect to him. He was slim and had excellent posture, possibly because he works every day standing up at his desk.

Visiting Gardner felt straight out of The Wizard of Oz. I was in the hurricane-strewn Midwest on a quest to meet an elderly magician. It turned out that Dorothy & co were an especially pertinent reference. I had not known this before I met him, but Gardner is a world expert on L. Frank Baum, the writer of The Wizard of Oz. Gardner told me that a decade previously he had even written a sequel in which Dorothy and friends go to Manhattan. It was reviewed in serious newspapers, if not very favourably. ‘It is written mainly for Oz fans,’ he said.

I gave him the G4G goody bag and asked how it felt to be the subject of a conference. ‘I am quite honoured, and surprised,’ he replied. ‘I am amazed at how it has grown.’ It quickly became clear that he was not entirely comfortable talking about his illustriousness among mathematicians. ‘I am not a mathematician,’ he said. ‘I am basically a journalist. Beyond calculus I am lost. That was the secret of my column’s success. It took me so long to understand what I was writing about that I knew how to write about it so most readers would understand it.’ When I learned that Gardner was not a proper mathematician I initially felt a little disappointed, as though the Wizard had pulled away the curtain.

Gardner’s preferred subject is magic. He described it as his principal hobby. He subscribes to magic magazines and – as much as his arthritis allows – practises tricks. He offered to show me what he said was the only sleight-of-hand card magic he had invented, called a ‘wink change’, in which the colour of a card is changed ‘in a wink’. He took a pack of cards and lodged a black card between the deck and the palm of his hand. Instantly, the black card became a red one. Gardner became interested in maths through ‘mathematical’ magic tricks, and it was magicians, not mathematicians, who formed his main social circle as a young adult. He said he liked magic because it developed a sense of wonder about the world. ‘You see a woman levitated and that reminds you that it is just as miraculous that she falls to the ground by gravity…you don’t realize that gravity is just as mysterious as a woman levitating.’ I asked him if maths gave him that same wonder. He replied, ‘Absolutely, yes.’

Gardner may be best known for his writings on maths, but they represent only a portion of his output. His first book was Fads and Fallacies, the first popular book to debunk pseudoscience. He has written on philosophy and published a serious novel about religion. His bestselling book is pan>The Annotated Alice, a timeless compendium of footnotes to Alice in Wonderland and Through the Looking-Glass. At 93, the output shows no signs of slowing down. He is due to publish a book of essays on G.K. Chesterton, and among his many other projects he is compiling a bumper book of word games.

Thanks to Gardner, recreational mathematics remains in very good shape. It is an exciting and diverse field that continues to give pleasure to people of all ages and nationalities, as well as inspiring serious research on serious problems. I had been slightly disheartened to learn that Gardner was not a mathematician, but as I left the Assisted Living Center, it struck me, after all, that it was brilliantly in the spirit of recreational maths that the man who now personifies it was only ever an enthusiastic amateur.